Раздел 3. Основы математического анализа

Тема 3.3. Интегральное исчисление функции одной действительной переменной Задание 25. Решение задач на применение методов интегрирования в неопределенном интеграле – 1 ч.

Цель: формирование умения находить неопределённые интегралы методами непосредственного интегрирования, подстановки, по частям.

Задание для самостоятельной внеаудиторной работы:

 25.1. Вспомните, какие основные методы интегрирования существуют. В чём заключается их сущность?

25.2. Определите, какой метод интегрирования необходимо использовать, и найдите неопределённые интегралы:

а) ; б) ; в) ; г) ; д) ; e) .

 25.3. Найдите неопределённые интегралы:

а) ; б) ; в) .

Методические указания по выполнению работы:

Если в задании не указан метод интегрирования, проанализируйте, можно ли использовать ранее изученные методы:

1. Метод непосредственного интегрирования используйте, если

• интеграл глобально представляет собой сумму или разность табличных функций;

• возможно раскрыть скобки или почленно поделить каждое слагаемое числителя на знаменатель для получения табличных функций.

Если в решении возникают проблемы – перечитайте методические указания к заданию 22.

2. Интегралы от «некоторых сложных» функций берите, если подынтегральная функция - функция вида f(kx+b), причём от f(x) можно взять табличный интеграл.

Используйте формулу: .

Если в решении возникают сложности – перечитайте методические указания к заданию 23.

3. Метод подстановки применяйте, если приняв какое-либо выражение за и под знаком интеграла окажется табличная функция, содержащая и, и производная и.

Подробный алгоритм Вы найдёте в методических указаниях к заданию 23.

4. Метод интегрирования по частям применяйте для нахождения интегралов

• вида , , , ;

• внутри которых один из множителей - логарифмическая или обратные тригонометрические функции (arcsinx, arccosx, arctgx, arcctgx).

Указания к решению таких примеров Вы найдёте в методических указаниях к заданию 24.

Список литературы:

1. Григорьев В.П. Элементы высшей математики: учеб. для студентов СПО / В.П. Григорьев, Ю.А. Дубинский. – М.: Академия, 2012.- 320 с. - Глава 7, п. 7.1, 7.2, стр. 150 – 156.

2. Валуцэ И.И. Математика для техникумов: учеб. пособие. / И.И. Валуцэ, Г.Д. Дилигул – М.: Наука, 1989.-576 с. - Глава 8, §45, 46, стр. 247 – 264.

3. Лисичкин В.Т. Математика: учеб. пособие для техникумов / В.Т. Лисичкин, И.Л. Соловейчик. – М.: Высш. школа, 1991. – 480 с. – Глава 5, §1-3, 5, стр. 290 – 306, 310 - 317.

Раздел 3. Основы математического анализа

Тема 3.3. Интегральное исчисление функции одной действительной переменной Задание 26. Нахождение определённых интегралов методом непосредственного интегрирования – 1 ч.

Цель: формирование умения находить определённые интегралы методом непосредственного интегрирования и как интегралы от некоторых сложных функций.

Задание для самостоятельной внеаудиторной работы:

 26.1. Выучите определение определенного интеграла. Разберите, в чём заключается техника непосредственного интегрирования в определённом интеграле. Ответьте на контрольные вопросы:

1. Что называют определенным интегралом ?

2. Какими свойствами обладает определенный интеграл?

3. Запишите формулу Ньютона-Лейбница.

4. Какова техника нахождения определённого интеграла при помощи формулы Ньютона-Лейбница?

5. Какова глобальные отличия определенного интеграла от неопределенного?

26.2. Найдите определённые интегралы методом непосредственного интегрирования и как интегралы от «некоторых сложных» функций:

а) 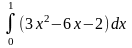; б) ; в) ; г) ; д) .

В ам известно, что одним из создателей интегрального исчисления был Готфрид Вильгельм Лейбниц.

Много гениальных открытий принадлежит Лейбницу. И действительно это была неординарная личность! Современников Лейбница поражали его фантастическая эрудиция, почти сверхъестественная память и удивительная работоспособность.

А

Г.В.Лейбниц

(1646-1716)

Г.В.Лейбниц

(1646-1716)

как же любовь? Лейбницу посчастливилось и здесь. Он полюбил одну из лучших германских женщин – первую королеву Пруссии.

Л ейбниц стал её учителем, когда юной принцессе было 12 лет. В 16 лет принцессу выдали замуж за тщеславного, недалёкого, любившего блеск и роскошь брандербургского принца Фридриха.

Серьёзная, вдумчивая, мечтательная принцесса не могла выносить пустой и бессмыссленной придворной жизни. Её отдушиной стала переписка с дорогим и любимым учителем. Эта переписка прекращалась лищь на время свиданий. В письмах теперь уже королевы при всей её сдержанности, нравственной чистоте и сознании долга перед мужем, никогда не ценившем и не понимавшем её, прорывалось сильное чувство.

В

королева Пруссии

ыполнив задание 26.2 и заменив получившиеся ответы буквами из таблицы, Вы узнаете, как звали королеву, рано ушедшую из жизни, которую искренне и беззаветно любил Готфрид Вильгельм Лейбниц.

Имя королевы:

а)	б)	в)	г)	д)

Карта ответов:

А	Е	И	Л	М	О	Н	Р	С	Ф	Я
			-0,5	0	3	-2		-4	0,5

26.3. Найдите определённые интегралы:

а) ; б) .

Методические указания по выполнению работы:

Определенным интегралом от функции f(x) на отрезке [a;b] называют предел интегральных сумм Sn (Sn= ) при п и λ→0 (λ=maxΔх_i, где i=1,2,…,п), который не зависит ни от способа разбиения отрезка [a;b] на части, ни от выбора точек ξ_i: = .

Числа а и b называются соответственно нижней и верхней границами интегрирования, f(x) - подынтегральной функцией, f(x)dx – подынтегральным выражением, х - переменной интегрирования, отрезок [a;b] – областью (отрезком) интегрирования.

При нахождении определённых интегралов используют следующие методы:

1. Непосредственное интегрирование – метод, основанный на использовании свойств определённого интеграла и формулы Ньютона-Лейбница.

Основные свойства определенного интеграла:

1. (k – const).

2. = ± .

3. = .

Формула Ньютона-Лейбница: = .

Для нахождения определённых интегралов методом непосредственного интегрирования можно использовать следующий алгоритм:

1. Найдите неопределённый интеграл от заданной функции (если возникают сложности, перечитайте методические указания к выполнению задания 22).

2. Выпишите получившуюся первообразную функции, в которую вместо слагаемого С запишите вертикальную черту с верхними и нижними границами интегрирования.

3. По формуле Ньютона-Лейбница в первообразную вместо переменной подставьте сначала верхнюю границу, затем запишите знак «минус», затем подставьте нижнюю границу интегрирования.

Советуем рассмотреть реализацию данного метода на примере:

Пример 1. Вычислите .

Решение. 1. Найдем неопределенный интеграл от заданной функции: .

2. Для нахождения определённого интеграла вместо константы С введём границы интегрирования:

= .

3. В полученную первообразную подставим сначала верхнюю, потом нижнюю границы интегрирования: =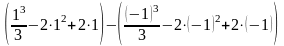 = . Раскроем скобки: .

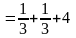
Ответ: .

2. Интегрирование некоторых сложных функций – метод, основанный на использовании техники интегрирования некоторых сложных функций и формулы Ньютона-Лейбница.

Для нахождения определённых интегралов от некоторых сложных функций можно использовать следующий алгоритм:

1. Найдите неопределённый интеграл от заданной функции, используя формулу (если возникают сложности, перечитайте методические указания к выполнению задания 20).

2. Для получившейся первообразной вместо слагаемого С запишите вертикальную черту с верхними и нижними границами интегрирования.

3. По формуле Ньютона-Лейбница в первообразную вместо переменной подставьте сначала верхнюю границу, затем знак «минус», затем нижнюю границу интегрирования.

Советуем рассмотреть реализацию данного метода на примере:

Пример 2. Вычислите .

Решение. 1.Сначала найдем неопределенный интеграл от заданной функции как интеграл от некоторой сложной функции, введя границы интегрирования: = .

2. Подставим сначала верхнюю, потом нижнюю границы интегрирования: = = - = - = + =2∙1+ = .

Ответ: = .

Список литературы:

1. Григорьев В.П. Элементы высшей математики: учеб. для студентов СПО / В.П. Григорьев, Ю.А. Дубинский. – М.: Академия, 2012.-320 с. - Глава 7, п. 7.3 - 7.6, стр. 156 – 167.

2. Валуцэ И.И. Математика для техникумов: учеб. пособие. / И.И. Валуцэ, Г.Д. Дилигул – М.: Наука, 1989.-576 с. - Глава 8, §47 - 50, стр. 267 – 283.

3. Лисичкин В.Т. Математика: учеб. пособие для техникумов / В.Т. Лисичкин, И.Л. Соловейчик. – М.: Высш. школа, 1991. – 480 с. – Глава 5, §6 - 7, стр. 318 - 331.