Задания для самостоятельной работы

Раздел 3. Основы математического анализа

Тема 3.3. Интегральное исчисление функции одной действительной переменной Задание 22. Нахождение неопределённых интегралов методом непосредственного интегрирования – 1 ч.

Цель: формирование умения находить неопределённые интегралы методом непосредственного интегрирования.

Задание для самостоятельной внеаудиторной работы:

 22.1. Проанализируйте, чем операция интегрирования отличается от дифференцирования. Выучите определение первообразной функции, основное свойство первообразных. Разберите, что называют неопределённым интегралом, каковы его основные свойства. Ответьте на контрольные вопросы:

1. Какую операцию называют интегрированием?

2. Что называют первообразной данной функции?

3. Сколько первообразных имеет любая функция?

4. В чём заключается основное свойство первообразных и каков его геометрический смысл?

5. Что называют неопределённым интегралом от функции у = f(x)?

6. Перечислите основные свойства неопределённого интеграла.

7. В чём заключается сущность метода непосредственного интегрирования?

22.2. Найдите интегралы методом непосредственного интегрирования:

а) ; б) ; в) ;

г) ; д) ; е) .

22.3. Найдите интегралы:

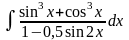а) ; б) ; в) ; г) .

Методические указания по выполнению работы:

Напомним, что суть дифференцирования: по заданной функции f(x) найти её производную. Интегрирование – операция, обратная дифференцированию: нахождение первоначальной функции F(x) по известной производной f(x).

Функция F(x) называется первообразной для функции f(x) на интервале (а;b), если для всех x из этого промежутка справедливо равенство: F'(x) = f(x).

Основное свойство первообразных: множество первообразных для функции f(x) задается формулой: F(x) + C, где С – константа.

Множество всех первообразных для функции f(x) называется неопределённым интегралом от функции f(x) и обозначается символом , т.е. = F(x) + C.

Свойства неопределенного интеграла:

1. a - const, a 0;

2. .

Для нахождения неопределённых интегралов существует несколько методов. Рассмотрим первый метод – метод непосредственного интегрирования.

В основе метода – сведение неопределенного интеграла к одному или нескольким табличным путем преобразований подынтегральной функции и применения свойств неопределенного интеграла.

Основные формулы интегрирования:

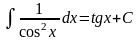
1. 2. 3. 4. 5. 6. 7. 8. 9. 10.

11. 12. , а – const 13. 14. 15. , а – const 16. 17. 18. 19.

При нахождении неопределенных интегралов методом непосредственного интегрирования используйте следующие рекомендации:

Проанализируйте, что представляет собой выражение под знаком интеграла.

• Если подынтегральное выражение представляет собой сумму или разность функций, то воспользуйтесь свойством: : представьте интеграл как сумму и разность соответствующих интегралов. Вынесите константы за знаки интегралов

( ) и возьмите табличные интегралы (разберите пример 1).

• Если в подынтегральном выражении встречаются члены вида , , , то с помощью формул = х^-п; _; приведите каждый одночлен к табличному интегралу: (разберите пример 2).

• Если подынтегральное выражение представляет собой произведение функций, попробуйте раскрыть скобки, выполнить преобразования и прийти к табличным интегралам (разберите пример 3).

• Если подынтегральное выражение представляет собой дробь, в знаменателе которой стоит одночлен, то разделите почленно каждое слагаемое числителя на знаменатель и придите к табличным интегралам (разберите пример 4).

• В остальных случаях попробуйте:

  • разложить числитель и знаменатель на множители и выполнить соответствующие сокращения;

  • добавить и вычесть из числителя какое-либо выражение, чтобы возможно было представить дробь как сумму двух дробей, одна из которых сокращается, а от другой можно взять табличный интеграл.

Пример 1. Найдите .

Решение. Воспользуемся свойствами неопределенного интеграла: представим интеграл как сумму и разность соответствующих интегралов: = .

Вынесем константы за знак интеграла: и воспользуемся табличными интегралами. Получим, что = = .

Ответ: = .

Пример 2. Найдите .

Решение. Каждое слагаемое, стоящее под знаком интеграла, представим в виде степени с рациональным показателем. Для этого применим следующие свойства степени: а^-п = ; . Тогда = .

Представим данный интеграл как сумму и разность интегралов, вынесем константы за знак интеграла: .

Воспользовавшись табличным интегралом , получим:

= = =

= = =

= = .

Ответ: = .

Пример 3. Найдите .

Решение. Раскрывая скобки и применяя табличные интегралы, получим:

= = = .

Ответ: = .

Пример 4. Найдите .

Решение. Разделим почленно каждое слагаемое числителя на знаменатель. Получим = = .

Представим данный интеграл как сумму и разность интегралов, вынесем константы за знак интеграла:

= = .

Ответ: = .

Список литературы:

1. Григорьев В.П. Элементы высшей математики: учеб. для студентов СПО / В.П. Григорьев, Ю.А. Дубинский. – М.: Академия, 2012.-320 с. - Глава 7, п. 7.1, 7.2, стр. 150 – 154.

2. Валуцэ И.И. Математика для техникумов: учеб. пособие. / И.И. Валуцэ, Г.Д. Дилигул – М.: Наука, 1989.-576 с. - Глава 8, §45 – 46, стр. 247 – 255.

3. Лисичкин В.Т. Математика: учеб. пособие для техникумов / В.Т. Лисичкин, И.Л. Соловейчик. – М.: Высш. школа, 1991. – 480 с. – Глава 5, §1-3, стр. 290 – 306.