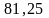- •Часть 2
- •Содержание
- •Пояснительная записка
- •Каждое задание включает в себя:
- •Рекомендации по выполнению разных видов
- •Как самостоятельно изучить теоретический материал
- •2. Как решать задачи (методика д. Пойа)
- •3. Как выполнить домашнюю контрольную работу
- •Задания для самостоятельной работы
- •Раздел 3. Основы математического анализа
- •Тема 3.3. Интегральное исчисление функции одной действительной переменной Задание 22. Нахождение неопределённых интегралов методом непосредственного интегрирования – 1 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.3. Интегральное исчисление функции одной действительной переменной Задание 23. Нахождение неопределённых интегралов методом подстановки – 2 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.3. Интегральное исчисление функции одной действительной переменной Задание 24. Нахождение неопределённых интегралов методом по частям – 1 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.3. Интегральное исчисление функции одной действительной переменной Задание 25. Решение задач на применение методов интегрирования в неопределенном интеграле – 1 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.3. Интегральное исчисление функции одной действительной переменной Задание 26. Нахождение определённых интегралов методом непосредственного интегрирования – 1 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.3. Интегральное исчисление функции одной действительной переменной Задание 27. Нахождение определённых интегралов методом подстановки – 1 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.3. Интегральное исчисление функции одной действительной переменной Задание 28. Нахождение определённых интегралов методом по частям – 1 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.3. Интегральное исчисление функции одной действительной переменной Задание 29. Нахождение определённых интегралов различными методами – 1 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.3. Интегральное исчисление функции одной действительной переменной Задание 30. Приложения определённого интеграла – 2 ч.
- •Виды фигур, площадь которых находится с помощью определенного интеграла
- •Раздел 3. Основы математического анализа
- •Тема 3.3. Интегральное исчисление функции одной действительной переменной Задание 31. Нахождение несобственных интегралов – 1 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.4. Дифференциальное исчисление функции нескольких действительных переменных Задание 32. Построение поверхности - графика функции двух переменных - в программе Microsoft Excel – 1 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.4. Дифференциальное исчисление функции нескольких действительных переменных Задание 33. Нахождение частных производных функции двух переменных – 2 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.4. Дифференциальное исчисление функции нескольких действительных переменных Задание 34. Нахождение частных производных второго порядка функции двух переменных – 1 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.5. Интегральное исчисление функции нескольких действительных переменных Задание 35. Нахождение повторных интегралов – 1 ч.
- •Петер Дирихле (1805-1859)
- •Раздел 3. Основы математического анализа
- •Тема 3.5. Интегральное исчисление функции нескольких действительных переменных Задание 36. Нахождение двойных интегралов по прямоугольной области и произвольной области 1 типа – 2 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.5. Интегральное исчисление функции нескольких действительных переменных Задание 37. Приложения двойных интегралов в геометрии – 2 ч.
- •Критерии оценки выполнения самостоятельной внеаудиторной работы
- •Список рекомендуемой литературы
Раздел 3. Основы математического анализа
Тема 3.5. Интегральное исчисление функции нескольких действительных переменных Задание 35. Нахождение повторных интегралов – 1 ч.
Цель: формирование умения вычислять повторные интегралы.
Задание для самостоятельной внеаудиторной работы:
35.1. Выучите определение повторного интеграла. Выясните, сколько типов повторного интеграла фактически существует. Проанализируйте, чем отличаются техники их вычисления.
35.2. Подумайте, могут ли внешние пределы интегрирования быть переменными. Постарайтесь аргументировать свой ответ.
35.3. Вычислите повторные интегралы:
а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)
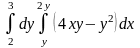 ;
д)
;
д)
 .
.
При вычислении повторных интегралов в ряде случаев используется формула Дирихле:
 .
.
П етер
Густав Лежён Дирихле (1805 - 1859) –
немецкий учёный, автор трудов по
интегральному исчислению, аналитической
теории чисел, теории рядов, математической
физике. В 1855 году П. Дирихле за свои
многочисленные заслуги был приглашён
в Геттинский университет в качестве
продолжателя самого Карла Гаусса. Работы
этого учёного в значительной мере
предопределили пути развития современной
математики.
етер
Густав Лежён Дирихле (1805 - 1859) –
немецкий учёный, автор трудов по
интегральному исчислению, аналитической
теории чисел, теории рядов, математической
физике. В 1855 году П. Дирихле за свои
многочисленные заслуги был приглашён
в Геттинский университет в качестве
продолжателя самого Карла Гаусса. Работы
этого учёного в значительной мере
предопределили пути развития современной
математики.
Ф
Петер Дирихле (1805-1859)
амилия «Дирихле» для немецкого языка достаточно необычная. Её происхождение обусловлено тем, что предки математика были выходцами из бельгийского городка. Выполнив задание 35.3. и заменив получившиеся ответы буквами из таблицы, Вы узнаете, какому бельгийскому городу фактически обязан своей фамилией П. Дирихле.Бельгийский город, которому обязан своей фамилией П. Дирихле:
а) |
б) |
в) |
г) |
д) |
|
|
|
|
|
Карта ответов:
Д |
И |
В |
Ю |
Л |
О |
М |
|
|
|
|
|
|
|
Ш |
А |
Т |
Е |
П |
Р |
Б |
|
|
|
|
|
|
|
Методические указания по выполнению работы:
Д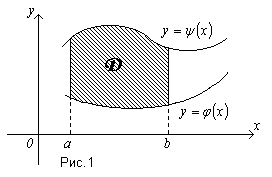 ля
успешного решения задач необходимо
знание следующего теоретического
материала:
ля
успешного решения задач необходимо
знание следующего теоретического
материала:
Пусть
на отрезке [a;b]
заданы непрерывные функции и
и
 такие, что
такие, что
 ,
,
 ,
и пусть на области
,
и пусть на области
 (рис.1) определена функция
(рис.1) определена функция
 .
.
Если
для любого фиксированного
 функция
,
как функция переменной
функция
,
как функция переменной
 ,
интегрируема на отрезке
,
интегрируема на отрезке
 ,
т.е. при любом
существует интеграл
,
т.е. при любом
существует интеграл
 ,
и функция
,
и функция
 интегрируема на отрезке [a;b],
то интеграл
интегрируема на отрезке [a;b],
то интеграл
 называется повторным интегралом
и обозначается через
называется повторным интегралом
и обозначается через

При
этом
называется внутренним интегралом;
 и
и
 -
внутренними, a
и b – внешними
пределами интегрирования.
-
внутренними, a
и b – внешними
пределами интегрирования.
Внутренние пределы интегрирования в повторном интеграле могут быть как постоянными, так и переменными. Внешние пределы интегрирования всегда являются конкретными числами.
Важно помнить, что глобально повторный интеграл представляет собой число.
Для вычисления
повторного интеграла
 надо последовательно взять два обычных
определенных интеграла. Сначала берется
внутренний интеграл
,
в котором переменная
надо последовательно взять два обычных
определенных интеграла. Сначала берется
внутренний интеграл
,
в котором переменная
 считается постоянной. Затем берется
внешний интеграл, т.е. полученное
выражение, зависящее от
,
интегрируется по
от a до b.
считается постоянной. Затем берется
внешний интеграл, т.е. полученное
выражение, зависящее от
,
интегрируется по
от a до b.
Рассмотрим пример вычисления повторного интеграла.
Пример 1.
Вычислите повторный интеграл

Решение. Сначала найдем внутренний интеграл, считая постоянным:
 .
.
Затем найдем внешний интеграл, т.е. полученную функцию проинтегрируем по . Тогда

Для сокращения записи все вычисления можно оформить следующим образом:

Ответ:
Для
функции
,
определённой на области
 понятие повторного интеграла вводится
аналогично рассмотренному ранее. При
этом повторный интеграл обозначается
через
понятие повторного интеграла вводится
аналогично рассмотренному ранее. При
этом повторный интеграл обозначается
через
 Вычисляется он также последовательным
взятием двух обычных определённых
интегралов. Но при вычислении внутреннего
интеграла
Вычисляется он также последовательным
взятием двух обычных определённых
интегралов. Но при вычислении внутреннего
интеграла
 постоянной считается переменная
.
А при нахождении внешнего интеграла
полученное выражение, зависящее от
,
интегрируется по
от c до d.
постоянной считается переменная
.
А при нахождении внешнего интеграла
полученное выражение, зависящее от
,
интегрируется по
от c до d.
Рассмотрим пример вычисления подобного повторного интеграла.
Пример
2. Вычислите повторный интеграл

Решение. Сначала найдем внутренний интеграл, считая постоянным:



 .
.
Затем
найдем внешний интеграл, т.е. полученную
функцию проинтегрируем по
.
Тогда




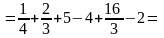

Ответ:

Список литературы:
1. Григорьев В.П. Элементы высшей математики: Учеб. для студ. учреждений СПО / В.П.Григорьев, Ю.А.Дубинский. - М.: Издательский центр "Академия", 2012. – 320с. – Глава 9, п.9.2, стр. 209 – 211.
2. Валуцэ И.И. Математика для техникумов на базе средней школы: Учебное пособие. / И.И. Валуцэ, Г.Д. Дилигул.– М.: Наука, 1989. – 576 с. – Глава 15, § 87, стр. 506.