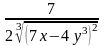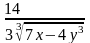- •Часть 2
- •Содержание
- •Пояснительная записка
- •Каждое задание включает в себя:
- •Рекомендации по выполнению разных видов
- •Как самостоятельно изучить теоретический материал
- •2. Как решать задачи (методика д. Пойа)
- •3. Как выполнить домашнюю контрольную работу
- •Задания для самостоятельной работы
- •Раздел 3. Основы математического анализа
- •Тема 3.3. Интегральное исчисление функции одной действительной переменной Задание 22. Нахождение неопределённых интегралов методом непосредственного интегрирования – 1 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.3. Интегральное исчисление функции одной действительной переменной Задание 23. Нахождение неопределённых интегралов методом подстановки – 2 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.3. Интегральное исчисление функции одной действительной переменной Задание 24. Нахождение неопределённых интегралов методом по частям – 1 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.3. Интегральное исчисление функции одной действительной переменной Задание 25. Решение задач на применение методов интегрирования в неопределенном интеграле – 1 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.3. Интегральное исчисление функции одной действительной переменной Задание 26. Нахождение определённых интегралов методом непосредственного интегрирования – 1 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.3. Интегральное исчисление функции одной действительной переменной Задание 27. Нахождение определённых интегралов методом подстановки – 1 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.3. Интегральное исчисление функции одной действительной переменной Задание 28. Нахождение определённых интегралов методом по частям – 1 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.3. Интегральное исчисление функции одной действительной переменной Задание 29. Нахождение определённых интегралов различными методами – 1 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.3. Интегральное исчисление функции одной действительной переменной Задание 30. Приложения определённого интеграла – 2 ч.
- •Виды фигур, площадь которых находится с помощью определенного интеграла
- •Раздел 3. Основы математического анализа
- •Тема 3.3. Интегральное исчисление функции одной действительной переменной Задание 31. Нахождение несобственных интегралов – 1 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.4. Дифференциальное исчисление функции нескольких действительных переменных Задание 32. Построение поверхности - графика функции двух переменных - в программе Microsoft Excel – 1 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.4. Дифференциальное исчисление функции нескольких действительных переменных Задание 33. Нахождение частных производных функции двух переменных – 2 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.4. Дифференциальное исчисление функции нескольких действительных переменных Задание 34. Нахождение частных производных второго порядка функции двух переменных – 1 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.5. Интегральное исчисление функции нескольких действительных переменных Задание 35. Нахождение повторных интегралов – 1 ч.
- •Петер Дирихле (1805-1859)
- •Раздел 3. Основы математического анализа
- •Тема 3.5. Интегральное исчисление функции нескольких действительных переменных Задание 36. Нахождение двойных интегралов по прямоугольной области и произвольной области 1 типа – 2 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.5. Интегральное исчисление функции нескольких действительных переменных Задание 37. Приложения двойных интегралов в геометрии – 2 ч.
- •Критерии оценки выполнения самостоятельной внеаудиторной работы
- •Список рекомендуемой литературы
Раздел 3. Основы математического анализа
Тема 3.4. Дифференциальное исчисление функции нескольких действительных переменных Задание 33. Нахождение частных производных функции двух переменных – 2 ч.
Цель: формирование умения находить частные производные и дифференциалы функций нескольких переменных.
Задание для самостоятельной внеаудиторной работы:
33.1. Выучите определение частной производной функции в точке. Выясните, чем отличается процесс дифференцирования функции по переменой х от дифференцирования по переменной у. Изучите технику нахождения частных производных функции. Проанализируйте, в чём заключается её отличие от техники обычного дифференцирования.
33.2. Найдите частные производные функций:
а)
 ;
б)
;
б)
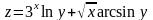 ;
в)
;
в)
 ;
;
г)
 ;
д)
;
д)
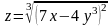 .
.
Для
частных производных по переменным х
и у в высшей математике часто
используется другое обозначение:
 и
и
 (круглым «
(круглым « »).
Выполнив задание 33.2.
и заменив получившиеся ответы буквами
из таблицы, Вы откроете имя и фамилию
блистательного учёного, который ввёл
это обозначение в общее употребление.
»).
Выполнив задание 33.2.
и заменив получившиеся ответы буквами
из таблицы, Вы откроете имя и фамилию
блистательного учёного, который ввёл
это обозначение в общее употребление.
Е го
вклад в математический и комплексный
анализ, линейную алгебру и другие разделы
математики огромен. Уже в первых своих
работах он проявил необычайный талант,
соединённый с необыкновенным трудолюбием.
По общему мнению, он не имел себе равных
и как педагог. В отличие от многих коллег
он старался стимулировать в студентах
творческие наклонности к самостоятельному
мышлению. Среди его учеников немало
выдающихся математиков.
го
вклад в математический и комплексный
анализ, линейную алгебру и другие разделы
математики огромен. Уже в первых своих
работах он проявил необычайный талант,
соединённый с необыкновенным трудолюбием.
По общему мнению, он не имел себе равных
и как педагог. В отличие от многих коллег
он старался стимулировать в студентах
творческие наклонности к самостоятельному
мышлению. Среди его учеников немало
выдающихся математиков.
Помимо других качеств, этого учёного отличало полное отсутствие завистливости. Когда его вечный научный соперник опубликовал работу, во многом перекрывавшую его собственные результаты, он ограничился замечанием: «Это выше моих работ и выше моих похвал».
Широко известна цитата учёного: «Единственной целью науки является честь человеческого разума, и с этой точки зрения вопрос о числе так же важен, как и вопрос о системе мира».
Имя и фамилия математика, который ввёл обозначение частной производной круглым « »:
а)
|
а)
|
б) |
б) |
|
в) |
в) |
г) |
г) |
д) |
|
|
|
|
|
|
|
|
|
|
Карта ответов:
К |
О |
С |
А |
|
|
|
|
Г |
У |
Э |
Л |
|
|
|
|
Р |
Е |
Д |
И |
|
|
|
|
А |
К |
О |
Ф |
|
|
|
|
Я |
Ж |
М |
Ь |
|
|
|
|
Б |
С |
Н |
Р |
|
|
|
|
33.3. Выучите определение полного дифференциала функции нескольких переменных и запомните формулу, которая используется для его нахождения.
33.4. Найдите полный дифференциал функции:
а) ;
б)
;
б) ;
в)
;
в) ;
г)
;
г)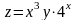 ;
д)
;
д)
 ;
;
е)
 ;
ж)
;
ж)
 .
.
Методические указания по выполнению работы:
Для успешного решения задач необходимо знание следующего теоретического материала:
Частной
производной функции двух переменных
по переменной х в точке
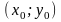 называется существующий предел отношения
частного приращения функции в этой
точке по переменной х к приращению
этой переменной при условии, что последнее
стремится к нулю:
называется существующий предел отношения
частного приращения функции в этой
точке по переменной х к приращению
этой переменной при условии, что последнее
стремится к нулю:

 или
или
 .
.
А налогично
определяется и обозначается частная
производная функции двух переменных
по переменной у в точке
:
налогично
определяется и обозначается частная
производная функции двух переменных
по переменной у в точке
:
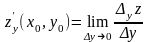 или
или
 .
.
Таким образом, частная производная функции двух переменных определяется как производная функции одной из этих переменных при условии постоянства значений другой переменной.
Частные производные функции трех и более переменных определяются аналогичным образом.
Поэтому техника нахождения частных производных ничем не отличается от обычного дифференцирования, нужно только помнить, что при дифференцировании функции нескольких переменных по какой – либо переменной все остальные переменные принимаются за постоянные.
Рассмотрим примеры нахождения частных производных функций двух переменных.
Пример
1. Найдите частные производные
функции
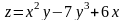 по переменным х и у.
по переменным х и у.
Решение. Для нахождения частной производной функции по переменной х рассматриваем у как постоянную величину. Используя правила дифференцирования разности и суммы, получаем:
 .
.
Для нахождения частной производной функции по переменной у рассматриваем х как постоянную величину. Используя правила дифференцирования разности и суммы, получаем:
 .
.
Ответ:
 ,
,
 .
.
Пример
2. Найдите частную производную
функции
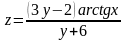 по переменной у.
по переменной у.
Решение. Для
нахождения частной производной функции
по переменной у рассматриваем х
как постоянную величину. Значит,
 как константу можно вынести за знак
частной производной. Используя правило
дифференцирования частного, окончательно
получим:
как константу можно вынести за знак
частной производной. Используя правило
дифференцирования частного, окончательно
получим:




 .
.
Ответ: .
Пример 3.
Найдите частную производную функции
 по переменной х.
по переменной х.
Решение. Для
нахождения частной производной функции
по переменной х рассматриваем у
как постоянную величину. Используя
правила дифференцирования суммы и
разности, а далее дифференцируя
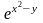 как сложную функцию, получаем:
как сложную функцию, получаем:

Ответ:

Главная часть
приращения функции
,
линейная относительно
 и
и
 ,
называется полным дифференциалом
этой функции и обозначается символом
dz:
,
называется полным дифференциалом
этой функции и обозначается символом
dz:
 .
.
Для нахождения полного дифференциала функции используется формула:
 .
.
Пример 4.
Найдите полный дифференциал функции
 .
.
Решение. Для нахождения полного дифференциала функции будем использовать формулу .
Найдём
- частную производную функции по
переменной х, рассматривая у, а
следовательно и
 ,
, как постоянные, применяя правило
дифференцирования суммы:
как постоянные, применяя правило
дифференцирования суммы:

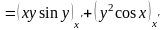
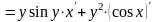

 .
.
Найдём
- частную производную функции по
переменной у, рассматривая х ,
а следовательно и,
 как постоянные, применяя правило
дифференцирования суммы, а для
дифференцирования
- произведения:
как постоянные, применяя правило
дифференцирования суммы, а для
дифференцирования
- произведения:
 .
.
Подставим и в формулу полного дифференциала, получим:
 .
.
Ответ: .
Список литературы:
1. Григорьев В.П. Элементы высшей математики: Учеб. для студ. учреждений СПО / В.П.Григорьев, Ю.А.Дубинский. - М.: Издательский центр "Академия", 2012. – 320с. – Глава 8, п.8.2, стр. 184 – 189.
2. Валуцэ И.И. Математика для техникумов на базе средней школы: Учебное пособие. / И.И. Валуцэ, Г.Д. Дилигул.– М.: Наука, 1989. – 576 с. – Глава 15, § 86, стр. 496-502.