Раздел 3. Основы математического анализа

Тема 3.4. Дифференциальное исчисление функции нескольких действительных переменных Задание 32. Построение поверхности - графика функции двух переменных - в программе Microsoft Excel – 1 ч.

Цель: формирование умения составлять таблицу значений для функции двух переменных и строить её график, используя возможности программы Microsoft Excel.

Задание для самостоятельной внеаудиторной работы:

 32.1. Дайте определение функции двух переменных. Что называют областью определения такой функции? Что называют графиком функции двух переменных? Какова геометрическая интерпретация графика функции двух переменных?

32.2.Задайте аналитически (с помощью формулы) функцию двух переменных , область определения которой . Используя возможности программы Microsoft Excel, cоставьте и заполните таблицу значений функции z, где переменные х и у принимают значения от -1 до 1 с шагом 0,2. Постройте соответствующий график.

32.3. Найдите и изобразите область определения функции двух переменных:

а) ; б) ; в) ;

г) ; д) .

Методические указания по выполнению работы:

Зависимость переменной z от пары значений переменных х и у, при которой каждой паре значений переменных х и у, принадлежащей некоторому множеству пар D, сопоставляется по определённому правилу f единственное значение переменной , называется функцией двух переменных, определенной на множестве D со значениями в .

Множество D пар значений, которые могут принимать независимые переменные х и у (значение функции при этом является числом), называется областью определения функции двух переменных.

Графиком функции , определенной в области D, называется множество точек (x;y;z) трехмерного пространства, у которых (x;y) принадлежит D и .

Как правило, график функции двух действительных переменных представляет собой некоторую поверхность в пространстве. Для её построения в программе Microsoft Excel рекомендуем использовать следующий алгоритм:

1. В программе Microsoft Excel cоставьте таблицу, где в строку заносите значение переменной х, в столбец - значения у. По условию задачи х и у принимают значения от -1 до 1 с шагом 0,2:

   у х	-1	-0,8	-0,6	-0,4	-0,2	0	0,2	0,4	0,6	0,8	1
   -1
   -0,8
   -0,6
   -0,4
   -0,2
   0
   0,2
   0,4
   0,6
   0,8
   1

2. Заполните ячейки таблицы значениями функции .

3. Используя мастер диаграмм, постройте соответствующую функции поверхность. Используйте правильные подписи числовых значений по осям 0х и 0у.

4. Оформите Вашу работу по образцу:

Функция <аналитическое задание>

Построил студент группы <номер группы>

<фамилия, имя>

<Таблица значений>

<Поверхность>

Если при выполнении работы у Вас возникают сложности, обратитесь к разбору примера 1.

Пример 1. Постройте график функции .

Решение. 1. Составим в программе Microsoft Excel таблицу значений функций .

Для этого в ячейки В1: L1 поместим значения переменной х от -1 до 1 с шагом 0,2.

В ячейки А2: А12 поместим значения переменной у от -1 до 1 с шагом 0,2.

Остальные ячейки B2:L12 должны содержать формулы для нахождения значений функции .

Например, формула в ячейке В2 имеет вид: = В1^2 – А2^2.

Можно использовать возможность таблиц подстановки!

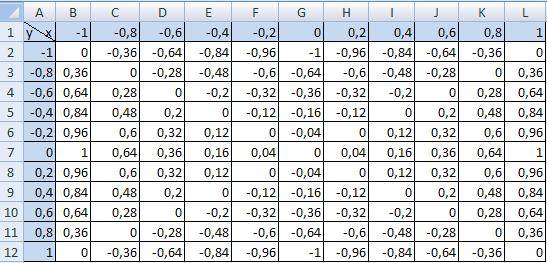
2. Используя мастер диаграмм, выберем тип диаграммы «поверхность», в качестве диапазона данных взяв диапазон ячеек B2:L12.

Необходимо изменить подписи по осям 0х и 0у, использовав вкладку «Конструктор», пункт «Выбрать данные».

График функции будет иметь следующий вид:

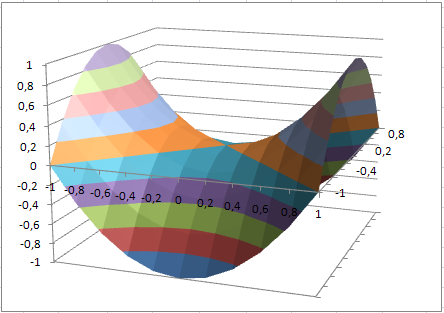
Не правда ли, очень напоминает седло?

И у Вас обязательно получится что-то интересное! Экспериментируйте! Желаем успеха!

Для различных функций двух переменных область определения имеет разный вид. Она может представлять собой конечную или бесконечную часть плоскости, ограниченную одной или несколькими непрерывными линиями – границами области. Возможен случай, когда какая – то из границ превращается в одну точку.

Пример 1. Найдите и изобразите область определения функции , зная, что х и у длины сторон прямоугольника, а S – его площадь.

Р ешение. С учетом геометрического смысла функции, её область определения представляет собой множество точек плоскости, координаты которых удовлетворяют системе 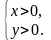Таким образом, - множество точек плоскости первой координатой четверти за исключением точек осей координат (рис.1).

Ответ: - множество точек плоскости первой координатой четверти за исключением точек осей координат.

Пример 2. Найдите и изобразите область определения функции .

Решение. Функция глобально представляет собой корень чётной степени, поэтому область её определения будем находить, учитывая, что подкоренное выражение неотрицательно. Таким образом, .

Изобразим область определения функции в прямоугольной декартовой системе координат. Для этого рассмотрим уравнение , преобразуем его к виду: . Данное уравнение является каноническим уравнением эллипса. Собственно по каноническому уравнению эллипса найдём большую a и малую b полуоси: , откуда , . Построим эллипс в прямоугольной декартовой системе координат.

Э ллипс разбивает множество точек плоскости на два подмножества: множество точек внутри эллипса и вне его. Определим, какое из них геометрически реализует область определения функции. Для этого возьмём произвольную точку, например, внутри эллипса и подставим её координаты в неравенство: . Получим: ; - верное неравенство. Таким образом, принадлежит области определения функции, а это означает, что область определения функции изображается множеством точек координатной плоскости внутри эллипса , включая точки эллипса (поскольку неравенство - нестрогое) (рис.2).

Ответ: - множество точек

Список литературы:

1. Григорьев В.П. Элементы высшей математики: учеб. для студентов СПО / В.П. Григорьев, Ю.А. Дубинский. – М.: Академия, 2012.-320 с. - Глава 8, п. 8.1, стр. 180 – 183.

2. Валуцэ И.И. Математика для техникумов: учеб. пособие. / И.И. Валуцэ, Г.Д. Дилигул – М.: Наука, 1989.-576 с. - Глава 15, §86, стр. 491 – 496.