Виды фигур, площадь которых находится с помощью определенного интеграла

№	Вид фигуры	Площадь фигуры	№	Вид фигуры	Площадь фигуры
1		Фигура расположена выше оси Ох (криволинейная трапеция) S=	4		Часть фигуры, огран. графиками двух функций, находится выше, а часть ниже оси Ох S= -
2		Фигура расположена ниже оси Ох S= или S=	5		Фигура ограничена графиками двух неотрицательных функций S= +
3		Часть фигуры, огран. графиком одной функции, находится выше, а часть ниже оси Ох S= +	6		Фигура ограничена графиками двух функций S=

Если при выполнении домашней контрольной работы возникают вопросы, разберите решение примера 1:

Пример 1. Вычислите площадь фигуры, ограниченной линиями и .

Р ешение. 1. Построим фигуру, ограниченную графиками функций и (рис. 1). Линия, задаваемая уравнением - прямая. Построим ее по двум точкам.

х	0	-3
у	3	0

Линия, задаваемая уравнением - парабола, ветви которой направлены вверх. Построим ее методом преобразований: выполним параллельный перенос графика функции на 1 единицу вверх.

Получили фигуру, ограниченную двумя графиками функций (заштрихована на рис. 1).

2. Согласно таблице «Виды фигур, площадь которых находится с помощью определенного интеграла» рассматриваемая фигура соответствует 6 типу (ограничена графиками двух функций). Её площадь можно вычислить по формуле:

S= , где f(x) – функция, ограничивающая фигуру "сверху" ( ),

а g(x) - функция, ограничивающая фигуру "снизу" ( ).

Границы интегрирования а и b в данном случае не следуют непосредственно из условия задачи. Решив уравнение , мы найдем абсциссы точек пересечения графиков соответствующих функций, т.е. а и b.

; . Найдем корни уравнения по теореме, обратной теореме Виета: х₁=-1 или х₂=2. Следовательно, а=-1, b=2.

Составим формулу для вычисления площади искомой фигуры: S= .

3. Вычислим значение площади: S= = = =

= = = =

= = = = = 4,5.

Ответ: S =4,5.

Список литературы:

1. Григорьев В.П. Элементы высшей математики: учеб. для студентов СПО / В.П. Григорьев, Ю.А. Дубинский. – М.: Академия, 2012.-320 с. - Глава 7, п. 7.7, стр. 169 – 170.

2. Валуцэ И.И. Математика для техникумов: учеб. пособие. / И.И. Валуцэ, Г.Д. Дилигул – М.: Наука, 1989.-576 с. - Глава 8, §52, стр. 290 – 294.

3. Лисичкин В.Т. Математика: учеб. пособие для техникумов / В.Т. Лисичкин, И.Л. Соловейчик. – М.: Высш. школа, 1991. – 480 с. – Глава 5, §8, стр. 290 – 331 - 342.

Раздел 3. Основы математического анализа

Тема 3.3. Интегральное исчисление функции одной действительной переменной Задание 31. Нахождение несобственных интегралов – 1 ч.

Цель: формирование умения находить несобственные интегралы I рода.

Задание для самостоятельной внеаудиторной работы:

 31.1. Какие интегралы называют несобственными интегралами I и II рода? В каких случаях несобственный интеграл называют сходящимся, а в каких расходящимся? В чём заключается техника нахождения несобственных интегралов I рода?

31.2. Вычислите несобственные интегралы или установите их расходимость:

а) ; б) ; в) ; г) .

31.3. Вычислите несобственные интегралы или установите их расходимость:

а) ; б) .

Методические указания по выполнению работы:

Несобственными будем считать интегралы двух видов:

1. Определённые интегралы от непрерывной функции, у которых один или оба пределы интегрирования равны бесконечности: , , 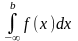. Их называют несобственными интегралами I рода.

2. Определённые интегралы от разрывной функции с конечными пределами интегрирования. Их называют несобственными интегралами II рода.

Для нахождения несобственных интегралов I рода будем использовать формулы:

= , = , = + (*), где с – произвольное число.

Если найденный предел равен конечному числу, то говорят, что несобственный интеграл сходится. Если указанный предел не существует или бесконечен, то говорят, что интеграл расходится.

Удобен следующий алгоритм нахождения несобственных интегралов:

1. Проверьте, является ли подынтегральная функция непрерывной на области интегрирования.

2. Используя одну из формул (*) от несобственного интеграла перейдите к пределу.

3. Отдельно найдите определённый интеграл с переменной границей а, b или с.

4. Подставьте полученное выражение под знак предела и найдите его значение.

5. Проанализируйте, является ли исходный интеграл сходящимся (значение предела – конечное число) или расходящимся (значение предела – бесконечность).

Рассмотрим примеры нахождения несобственных интегралов I рода.

Пример 1. Вычислите несобственный интеграл или установить его расходимость: .

Решение. 1. Подынтегральная функция непрерывна на промежутке (0;+∞].

2. Воспользуемся формулой: = . Тогда = .

3. Отдельно найдём определённый интеграл с переменной границей b:

= = =

4. Подставим полученное выражение под знак предела и найдём его значение:

= =∞.

5. Так как значение предела бесконечность, несобственный интеграл расходится.

Ответ: расходится.

Пример 2. Вычислите несобственный интеграл или установить его расходимость: .

Решение. 1. Подынтегральная функция 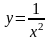непрерывна на промежутке (-∞;-1].

2. Воспользуемся формулой: = . Тогда = .

3. Отдельно найдём определённый интеграл с переменной границей а: = . Избавимся от знака "минус", поменяв границы интегрирования местами: = = = .

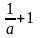4. Подставим полученное выражение под знак предела и найдём его значение:

= =1.

5. Поскольку значение предела – конечное число, то несобственный интеграл сходится.

Ответ: =1.

Список литературы:

1. Григорьев В.П. Элементы высшей математики: учеб. для студентов СПО / В.П. Григорьев, Ю.А. Дубинский. – М.: Академия, 2012.-320 с. - Глава 7, п. 7.8, стр. 173 – 175.