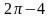- •Часть 2
- •Содержание
- •Пояснительная записка
- •Каждое задание включает в себя:
- •Рекомендации по выполнению разных видов
- •Как самостоятельно изучить теоретический материал
- •2. Как решать задачи (методика д. Пойа)
- •3. Как выполнить домашнюю контрольную работу
- •Задания для самостоятельной работы
- •Раздел 3. Основы математического анализа
- •Тема 3.3. Интегральное исчисление функции одной действительной переменной Задание 22. Нахождение неопределённых интегралов методом непосредственного интегрирования – 1 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.3. Интегральное исчисление функции одной действительной переменной Задание 23. Нахождение неопределённых интегралов методом подстановки – 2 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.3. Интегральное исчисление функции одной действительной переменной Задание 24. Нахождение неопределённых интегралов методом по частям – 1 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.3. Интегральное исчисление функции одной действительной переменной Задание 25. Решение задач на применение методов интегрирования в неопределенном интеграле – 1 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.3. Интегральное исчисление функции одной действительной переменной Задание 26. Нахождение определённых интегралов методом непосредственного интегрирования – 1 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.3. Интегральное исчисление функции одной действительной переменной Задание 27. Нахождение определённых интегралов методом подстановки – 1 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.3. Интегральное исчисление функции одной действительной переменной Задание 28. Нахождение определённых интегралов методом по частям – 1 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.3. Интегральное исчисление функции одной действительной переменной Задание 29. Нахождение определённых интегралов различными методами – 1 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.3. Интегральное исчисление функции одной действительной переменной Задание 30. Приложения определённого интеграла – 2 ч.
- •Виды фигур, площадь которых находится с помощью определенного интеграла
- •Раздел 3. Основы математического анализа
- •Тема 3.3. Интегральное исчисление функции одной действительной переменной Задание 31. Нахождение несобственных интегралов – 1 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.4. Дифференциальное исчисление функции нескольких действительных переменных Задание 32. Построение поверхности - графика функции двух переменных - в программе Microsoft Excel – 1 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.4. Дифференциальное исчисление функции нескольких действительных переменных Задание 33. Нахождение частных производных функции двух переменных – 2 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.4. Дифференциальное исчисление функции нескольких действительных переменных Задание 34. Нахождение частных производных второго порядка функции двух переменных – 1 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.5. Интегральное исчисление функции нескольких действительных переменных Задание 35. Нахождение повторных интегралов – 1 ч.
- •Петер Дирихле (1805-1859)
- •Раздел 3. Основы математического анализа
- •Тема 3.5. Интегральное исчисление функции нескольких действительных переменных Задание 36. Нахождение двойных интегралов по прямоугольной области и произвольной области 1 типа – 2 ч.
- •Раздел 3. Основы математического анализа
- •Тема 3.5. Интегральное исчисление функции нескольких действительных переменных Задание 37. Приложения двойных интегралов в геометрии – 2 ч.
- •Критерии оценки выполнения самостоятельной внеаудиторной работы
- •Список рекомендуемой литературы
Раздел 3. Основы математического анализа
Тема 3.3. Интегральное исчисление функции одной действительной переменной Задание 28. Нахождение определённых интегралов методом по частям – 1 ч.
Цель: формирование умения находить определённые интегралы методом по частям.
Задание для самостоятельной внеаудиторной работы:
28.1. Разберите, в чём заключается сущность использования метода по частям в определённом интеграле.
28.2. Найдите определённые интегралы методом по частям:
а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)
 .
.
Г
Арифметическая машина Лейбница
отфрид Лейбниц был не только гениальным математиком, но ещё и талантливым изобретателем. Вам, как студентам компьютерных специальностей, известно, что первую механическую счетную машину сконструировал в 1642 г. французский ученый Блез Паскаль. Машина Паскаля могла только складывать и вычитать.Лейбниц пытался сначала лишь улучшить машину Паскаля, но понял, что для выполнения операций умножения и деления необходим совершенно иной принцип. Можно понять гордость Лейбница, писавшего впоследствии «Мне посчастливилось построить такую арифметическую машину, которая совершенно отлична от машины Паскаля, поскольку дает возможность мгновенно выполнять умножение и деление над огромными числами». Арифметическая машина Лейбница была первой в мире машиной, предназначенной для выполнения четырех действий арифметики.
Интересно, что один из первых экземпляров «арифметического инструмента» Лейбниц намеревался подарить Петру I, но машина оказалась неисправной, а механик ученого не смог ее починить в короткий срок. Лейбница живо интересовал молодой царь далекой Московии, которого он считал выдающимся реформатором. Петр встречался и переписывался с Лейбницем, обсуждал с ним проект организации Академии наук в Петербурге и развертывания системы образования в России.
Выполнив задание 28.2 и заменив получившиеся ответы буквами из таблицы, Вы узнаете, в каком году Лейбницем была сконструирована первая счётная машина для умножения и деления.
Год:
а) |
б) |
в) |
г) |
|
|
|
|
Карта ответов:
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
-1 |
1 |
0 |
|
|
|
|
|
|
|
28.3. Найдите определённые интегралы:
а)
 ;
б)
;
б)
 .
.
Методические указания по выполнению работы:
Интегрирование
по частям - осуществляется
с использованием формулы
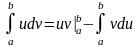 .
.
Рекомендации по выбору u и dv, а также алгоритм нахождения интеграла методом по частям были подробно разобраны в методических указаниях к выполнению задания №21.
Рассмотрим примеры применения метода интегрирования по частям в определенном интеграле.
Пример
1. Найдите
 .
.
Решение.
1. Исходный интеграл имеет вид
 ,
следовательно, за и принимаем
многочлен (и=х), остальные множители
примем за dv: dv=
,
следовательно, за и принимаем
многочлен (и=х), остальные множители
примем за dv: dv=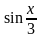 dx.
dx.
2. Находим dи=и'dx: dи=х'dx=dx.
Находим
:
 =
= (интеграл от некоторой сложной функции,
полагаем С=0).
(интеграл от некоторой сложной функции,
полагаем С=0).
3.
По формуле
имеем:
=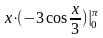 -
- =
=
=
= +
+
+
+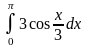 .
Преобразуем каждое слагаемое отдельно:
.
Преобразуем каждое слагаемое отдельно:
= =
= -
- =0-
=0- =
= .
.
= =
= -
- =
= -9
-9 =
= .
.
Тогда
исходный интеграл равен
=
+
= .
.
Ответ: = .
Список литературы:
1. Григорьев В.П. Элементы высшей математики: учеб. для студентов СПО / В.П. Григорьев, Ю.А. Дубинский. – М.: Академия, 2012.-320 с. - Глава 7, п. 7.3 - 7.6, стр. 167.
2. Валуцэ И.И. Математика для техникумов: учеб. пособие. / И.И. Валуцэ, Г.Д. Дилигул – М.: Наука, 1989.-576 с. - Глава 8, §47 - 50, стр. 267 – 283.
3. Лисичкин В.Т. Математика: учеб. пособие для техникумов / В.Т. Лисичкин, И.Л. Соловейчик. – М.: Высш. школа, 1991. – 480 с. – Глава 5, §6 - 7, стр. 318 - 331.