
2. Сила ампера. Сила лоренца
В магнитном поле на движущийся заряд действует сила Лоренца:
![]() (28)
(28)
где q электрический заряд;
![]()
его скорость;
его скорость;
магнитная индукция внешнего поля.
Н аправление
силы Лоренца определяется исходя из
определения векторного произведения
или по правилу левой руки (при этом надо
учитывать знак заряда). Это правило
заключается в следующем: четыре пальца
левой руки располагают по направлению
скорости частицы, при этом линии магнитной
индукции должны входить в ладонь, а
отогнутый на 90
большой палец укажет направление силы
Лоренца, действующей на положительно
заряженную частицу. Если частица имеет
отрицательный заряд q,
то сила Лоренца направлена в противоположную
сторону (рис. 11).
аправление
силы Лоренца определяется исходя из
определения векторного произведения
или по правилу левой руки (при этом надо
учитывать знак заряда). Это правило
заключается в следующем: четыре пальца
левой руки располагают по направлению
скорости частицы, при этом линии магнитной
индукции должны входить в ладонь, а
отогнутый на 90
большой палец укажет направление силы
Лоренца, действующей на положительно
заряженную частицу. Если частица имеет
отрицательный заряд q,
то сила Лоренца направлена в противоположную
сторону (рис. 11).
Сила Лоренца всегда направлена перпендикулярно скорости заряженной частицы, поэтому работы над частицей не совершает.
На
проводники с током, находящиеся в
магнитном поле, действуют силы, называемые
силами Ампера. Сила Ампера, приложенная
к элементу проводника с током
![]() ,
определяется по формуле:
,
определяется по формуле:
![]() .
(29)
.
(29)
В частности, если поле однородно, то на прямолинейный проводник с током длиной ℓ действует сила:
FA = IВℓsin, (30)
г де
угол между направлениями тока и магнитной
индукции.
де
угол между направлениями тока и магнитной
индукции.
Направление силы Ампера также определяется по правилу левой руки, которое формулируется следующим образом: четыре пальца левой руки располагают по направлению тока в проводнике, при этом линии магнитной индукции должны входить в ладонь, а отогнутый на 90 большой палец укажет направление силы Ампера, действующей на проводник с током (рис. 12).
Примеры решения задач
Задача 4. Прямолинейный проводник с током 1 А находится в однородном магнитном поле и поле тяжести. Проводник расположен горизонтально и перпендикулярно линиям индукции магнитного поля и находится в равновесии. С каким ускорением начнет двигаться проводник, если по нему будет течь ток 0,5 А в прежнем направлении?
Дано: I1 = 1 A; I2 = 0,5 A |
|
Р
|
a – ? |
||
|
|
Рис. 13 Рис. 14 |
Чтобы
горизонтально расположенный проводник
не падал в магнитном поле под действием
силы тяжести
![]() ,
индукция магнитного поля
должна быть направлена горизонтально
и перпендикулярно проводнику (рис. 13).
В этом случае силу тяжести уравновесит
сила Ампера
,
индукция магнитного поля
должна быть направлена горизонтально
и перпендикулярно проводнику (рис. 13).
В этом случае силу тяжести уравновесит
сила Ампера
![]() ,
направление которой определяем по
правилу левой руки.
,
направление которой определяем по
правилу левой руки.
Запишем условие равновесия проводника с током I1 в векторном виде и в проекциях на ось Оу:
+ = 0; (31)
![]() + mg
= 0; (32)
+ mg
= 0; (32)
mg = . (33)
Силу Ампера найдем через характеристики проводника и поля:
![]() (34)
(34)
где = 90, sin 90 = 1;
![]() длина проводника.
длина проводника.
Подставим формулу (34) в уравнение (33):
mg
=
![]() .
(35)
.
(35)
Если силу тока в
проводнике уменьшить, то сила Ампера
![]() будет мень-ше силы тяжести и проводник
начнет падать с ускорением (рис. 14).
будет мень-ше силы тяжести и проводник
начнет падать с ускорением (рис. 14).
Запишем уравнение движения проводника в векторном виде:
![]() =
+
=
+
![]() .
(36)
.
(36)
Перепишем уравнение (36) в проекциях на ось у:
maу = mg . (37)
Силу Ампера найдем через характеристики проводника и поля:
![]() (38)
(38)
![]()
Подставим формулу (38) в выражение (37):
maу
= mg
![]() .
(39)
.
(39)
В уравнении (39) неизвестны магнитная индукция, масса и длина проводника. От этих неизвестных можно избавиться, если воспользоваться условием равновесия проводника, когда по нему течет ток I1 (см. рис. 13).
Подставим формулу (35) в уравнение (39):
maу
=
=
 ;
(40)
;
(40)
maу
= mg .
(41)
.
(41)
Исходя из уравнения (41) получим расчетную формулу:
aу = g . (42)
Введем данные задачи в формулу (42) и получим значение проекции ускорения:
aу = 9,8(1/1 + 0,5) = 4,8 (м/с2).
Ответ: проводник будет двигаться вертикально вниз с ускорением 4,8 м/с2.
Задача 5. Альфа-частица влетела в однородное магнитное поле с индукцией 300 мТл перпендикулярно к направлению линий индукции, после этого она стала двигаться по окружности радиусом 0,2 мм. Определить величину скорости и период обращения частицы по окружности.
Дано: B = 300 мТл; R = 0,2 мм; m = 6,641027 кг; q = 3,21019 Кл; = 90 |
СИ 0,3 Тл 2104 м |
Решение.
|
v – ? T – ? |
На движущийся заряд в магнитном поле действует сила Лоренца:
![]() .
(43)
.
(43)
Направление силы Лоренца определяется по правилу левой руки. Как видно из рис. 15, сила Лоренца перпендикулярна скорости, поэтому она вызывает движение -частицы по окружности радиусом R.
На -частицу
также действуют сила тяжести
![]() ,
но она значительно меньше силы Лоренца,
поэтому силой тяжести можно пренебречь.
,
но она значительно меньше силы Лоренца,
поэтому силой тяжести можно пренебречь.
При таком движении -частицы сила Лоренца является центростремительной.
Скорость, с которой -частица влетела в магнитное поле, найдем из уравнения движения:
![]() . (44)
. (44)
Если векторы равны, то равны и их модули:
![]() , (45)
, (45)
здесь учтено, что центростремительное ускорение
![]() . (46)
. (46)
Из формулы (46) выразим скорость:
 . (47)
. (47)
Подставив в формулу (47) данные задачи, получим:
 (м/с)
= 2,9 (км/с).
(м/с)
= 2,9 (км/с).
Период обращения частицы:
![]() . (48)
. (48)
Подставим численные значения R и v в формулу (48) и рассчитаем период:
 (с).
(с).
Ответ: v = 2,9 км/с; Т = 0,43 с.
Задача 6. Электрон, имея скорость 3 Мм/с, влетел в однородное магнитное поле с индукцией 40 мТл под углом 30 к направлению линий индукции. Определить радиус и шаг винтовой линии, по которой будет двигаться электрон.
Дано: v = 3 Мм/с; B = 40 мТл; = 30; qе = 1,61019 Кл; mе = 9,11031 кг |
СИ 3106 м/с 4102 Тл |
Р
|
R – ? h – ? |
На движущийся заряд в магнитном поле действует сила Лоренца:
![]() . (49)
. (49)
Так как сила Лоренца
перпендикулярна вектору скорости, то
модуль скорости не будет изменяться
под действием этой силы, но при постоянной
величине скорости электрона остается
постоянным и модуль силы Лоренца.
Постоянная сила, перпендикулярная
скорости, вызывает движение по окружности.
Следовательно, электрон, влетевший в
магнитное поле, будет двигаться по
окружности в плоскости, перпендикулярной
линиям индукции, со скоростью, равной
поперечной составляющей
![]() скорости (рис. 16); одновременно он будет
двигаться и вдоль поля со скоростью
v||:
скорости (рис. 16); одновременно он будет
двигаться и вдоль поля со скоростью
v||:
=
v
![]() (50)
(50)
v||
=
v
![]() . (51)
. (51)
В результате одновременного движения по окружности и по прямой электрон будет двигаться по винтовой линии.
Радиус окружности, по которой движется электрон, найдем из уравнения движения:
. (52)
Если векторы равны, то равны и их модули:
 , (53)
, (53)
здесь учтено, что центростремительное ускорение
![]() . (54)
. (54)
Из формул (50) и (53) найдем радиус:
 (55)
(55)
Подставив в формулу (55) данные задачи, получим:
 =
0,21 (мм).
=
0,21 (мм).
Шаг винтовой линии h равен пути, пройденному электроном вдоль поля со скоростью v|| за время, которое понадобится электрону для того, чтобы совершить один оборот:
![]() (56)
(56)
где Т период обращения электрона,
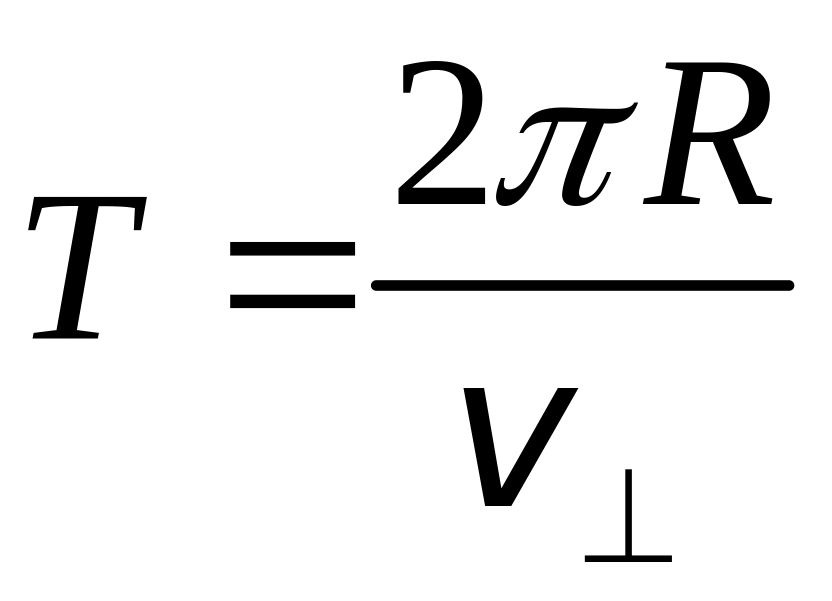 . (57)
. (57)
Подставив выражения (51) и (57) в формулу (56), получим расчетную формулу для определения шага винтовой линии:
h = 2rctg. (58)
Подставим в формулу (58) численные значения R и :
![]() (мм).
(мм).
Ответ: R = 0,21 мм; h = 2,3 мм.

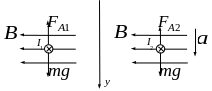 ешение.
ешение.
 ешение.
ешение.