
Министерство транспорта Российской Федерации
Федеральное агентство железнодорожного транспорта
Омский государственный университет путей сообщения
______________________________________________
О. И. Сердюк
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ
ПРИ ИЗУЧЕНИИ РАЗДЕЛА ФИЗИКИ «ЭЛЕКТРОМАГНЕТИЗМ»
Утверждено редакционно-издательским советом университета
Омск 2009
УДК 537.8 (075.8)
ББК 22.334я73
С32
Методические указания для самостоятельной работы студентов при изучении раздела физики «Электромагнетизм» / О. И. Сердюк. Омский гос. ун-т путей сообщения. Омск, 2009. 32 с.
Составлены в соответствии с программой курса общей физики для технических вузов, содержат краткие теоретические сведения по разделу физики «Электромагнетизм» и рекомендации по их изучению, приведены основные законы и формулы, примеры решения типовых задач, которые должны уметь решать студенты в объеме учебной программы.
Предназначены для самостоятельной работы студентов первого курса очной формы обучения.
Библиогр.: 4 назв. Рис. 23.
Рецензенты: доктор техн. наук, профессор В. Т. Черемисин;
канд. техн. наук, доцент А. И. Блесман.
_ ________________________
________________________
© Омский гос. университет
путей сообщения, 2009
ОГЛАВЛЕНИЕ
Введение 5
1. Магнитное поле. Магнитная индукция. Принцип суперпозиции
магнитных полей 6
2. Сила Ампера. Сила Лоренца 13
3. Поток вектора магнитной индукции. Работа по перемещению
проводника и контура с током в магнитном поле 19
4. Явление электромагнитной индукции. Закон Фарадея-Ленца 24
5. Индуктивность соленоида. Энергия магнитного поля 29
Библиографический список 31
3

ВВЕДЕНИЕ
Изучение физики формирует у студентов основные представления о важнейших физических закономерностях, лежащих в основе работы механи-ческих, тепловых, электрических, магнитных, оптических приборов и устройств, эксплуатируемых на железнодорожном транспорте.
Успешное изучение общего курса физики в вузе невозможно без умения применять физические закономерности на практике, однако именно решение задач вызывает наибольшие затруднения у студентов. Это связано с тем, что решение конкретных задач требует не только знания физических законов, но и определенного методического подхода.
Цель данных методических указаний – оказать помощь студентам в самостоятельном усвоении основных физических величин и законов, а также методики решения типовых задач по разделу «Электромагнетизм».
В методических указаниях содержатся краткие теоретические сведения по разделу «Электромагнетизм» [1 – 4] и даны рекомендации по решению типовых задач по основным темам электромагнетизма. Разнообразие представленных задач позволит студенту ознакомиться с различными типами физических задач по данной теме и методами их решения, лучше понять физические законы и усвоить основные положения и законы электромагнетизма, получить навыки применения изученных положений в практической инженерной деятельности. Кроме того, приведенные примеры решения задач помогут студентам, не усвоившим какую-либо тему по разделу «Электромагнетизм», самостоятельно разобраться в методике решения задач определенного типа.
1. Магнитное поле. Магнитная индукция.
ПРИНЦИП СУПЕРПОЗИЦИИ МАГНИТНЫХ ПОЛЕЙ
Магнитное
поле создается движущимися зарядами
или электрическими токами.
Посредством магнитного поля осуществляется
взаимодействие между токами
или движущимися зарядами. Для количественной
характеристики магнитного
поля служит физическая величина –
магнитная индукция
![]() ,
которая
является силовой характеристикой поля.
В СИ магнитная индукция измеряется в
теслах (Тл).
,
которая
является силовой характеристикой поля.
В СИ магнитная индукция измеряется в
теслах (Тл).
Магнитное поле в отличие от электростатического носит вихревой характер. Графически магнитное поле изображают при помощи замкнутых линий магнитной индукции. Линией магнитной индукции называют линию, касательная к которой в каждой точке совпадает с направлением вектора магнитной индукции. Изображая магнитные линии, можно наглядно представить, как меняется в пространстве магнитная индукция поля по величине и направлению.
Линии индукции магнитного поля прямого проводника с током имеют вид окружностей, охватывающих провод (рис. 1).
Направление вектора магнитной индукции определяется с помощью правила буравчика: если буравчик с правой резьбой ввинчивать по направлению тока (рис. 2), то направление вращения рукоятки буравчика совпадает с направлением индукции магнитного поля, создаваемого этим током.
Касательная в любой точке линии позволяет определить направление вектора магнитной индукции (рис. 3).

Рис. 1 Рис. 2 Рис. 3
Магнитное поле нити с током в форме кольца показано на рис. 4. Линии индукции поля изображены в плоскости, перпендикулярной витку и проходящей через ось симметрии.
Направление вектора магнитной индукции на оси ОО, в частности в центре витка с током (рис. 5) можно определить также по правилу буравчика: если буравчик с правой резьбой вращать по направлению тока, то поступательное движение буравчика покажет направление .
Магнитное поле соленоида изображено на рис. 6. Направление вектора магнитной индукции на оси соленоида определяется так же, как и в случае кругового тока.

Рис. 4 Рис. 5 Рис. 6
При решении задач этого раздела надо иметь в виду, что для магнитного поля в вакууме и воздухе, как и для электрического, справедлив принцип суперпозиции полей: если имеется несколько токов, каждый из которых создает магнитное поле, то магнитные поля не искажают друг друга, а магнитная индукция результирующего поля равна векторной сумме магнитных индукций полей, созданных каждым током в отдельности:
 (1)
(1)
Для записи векторного уравнения (1) в скалярной форме выбирают координатные оси х, у, z и находят проекции вектора на эти оси:
вх = в1х + в2х + ... + вnх; (2)
Ву=В1у + В2у + ... + Вny; (3)
вz = в1z + в2z + ... + вnz. (4)
При решении задач на принцип суперпозиции следует отметить, что круговые витки с током, перпендикулярные плоскости рисунка, принято изображать следующим образом: сторона витка, на которой ставится стрелка, указывающая направление тока, должна быть ближайшей «к нам» (см. рис. 3).
Примеры решения задач
Задача 1. Два бесконечно длинных параллельных проводника с токами I1 и I2 расположены так, как показано на рис. 7. Найти величину магнитной индукции поля в точке А, расположенной посередине между проводами, если I1 = 4 А, I2 = 2 А, а = 10 см
Дано: I1 = 4 A; I2 = 2 A; a = 10 см |
С
0,1 м |
Решение.
Применив правило
правого винта, определим направление
векторов индукции
|
В – ? |
||
|
|
Для нахождения магнитной индукции в точке А воспользуемся принципом суперпозиции магнитных полей. |
Запишем принцип суперпозиции в векторном виде:
= + . (5)
Выбрав координатную ось х, направленную вниз, запишем выражение (5) в проекциях на ось х:
B = B1 B2. (6)
Магнитные индукции В1 и В2 бесконечно длинных проводников с током определим по формулам:
![]() (7)
(7)
![]() (8)
(8)
где km коэффициент пропорциональности, km = 107 Н/А2.
Подставив формулы (7) и (8) в выражение (6), получим:
![]() (9)
(9)
Вычислим значение магнитной индукции, подставив данные задачи в уравнение (9):
![]() (Тл).
(Тл).
Ответ: В = 4 мкТл.
Задача 2. Два бесконечно длинных проводника с токами I1 и I2 и круговой контур с током I3 расположены так, как показано на рис. 8. Найти магнитную индукцию поля в точке А, если а = 10 см, радиус витка R = 5 см, I1 = 2 А, I2 = 4А, I3 = 3 А.
Дано: I1 = 2 A; I2 = 4 A; I3 = 3 A; R = 5 см; a = 10 см |
СИ
0,05 м 0,1 м |
Р
|
В – ? |
Применив правило
правого винта, определим
направление
векторов индукции
,
и
![]() ,
создаваемых каждым током в отдельности.
Для нахождения магнитной индукции
в точке А воспользуемся принципом
суперпозиции магнитных полей.
,
создаваемых каждым током в отдельности.
Для нахождения магнитной индукции
в точке А воспользуемся принципом
суперпозиции магнитных полей.
Запишем принцип суперпозиции в векторном виде:
=
+
+
![]() .
(10)
.
(10)
Все векторы
![]() ,
,
,
,
![]() лежат в одной плоскости.
лежат в одной плоскости.
Запишем выражение (10) в проекциях на оси х и у:
Bx = B3 B2sin B1sin; (11)
By = B2cos B1cos; (12)
Bz = 0, (13)
где = 30.
Значения магнитных индукций В1, В2 и В3 определим по следующим формулам:
(14)
![]() (15)
(15)
 (16)
(16)
Подставив формулы (14), (15) и (16) в выражения (11) и (12), получим систему уравнений:

 (17)
(17)
Рассчитаем проекции магнитной индукции, подставив данные задачи в выражения (17):
 (Тл);
(Тл);
![]() (Тл).
(Тл).
Величина магнитной индукции в точке А может быть определена через ее проекции:
![]() (18)
(18)
![]() (Тл).
(Тл).
Ответ: 1) проекции вектора магнитной индукции имеют следующие значения: = {2,6 мкТл; 3,5 мкТл; 0}; 2) величина вектора магнитной индукции В = 4,4 мкТл.
Задача 3. Бесконечно длинный проводник с током I1 и контур с током I2 в виде равностороннего треугольника со стороной а расположены так, как показано на рис. 9. Найти магнитную индукцию поля в точке пересечения высот треугольника, если а = 20 см, I1 = 20 А, I2 = 3 А.
Дано: I1 = 20A; I2 = 3 A; a = 20 см |
СИ
0,2 м |
Р
|
В – ? |
||
|
|
|
|
|
|
По правилу правого винта найдем направления векторов индукции, создаваемых токами I1 и I2. Разобьем контур ECD на три участка (EC, CD и DE) и рассмотрим их как независимые прямые проводники с током конечной длины. Все векторы магнитной индукции перпендикулярны плоскости рис. 9, поэтому координатную ось х удобно выбрать в этом же направлении – «от нас».
Для нахождения магнитной индукции в точке А воспользуемся принципом суперпозиции магнитных полей.
Запишем принцип суперпозиции в векторном виде:
=
+![]() +
+![]() +
+![]() .
(19)
.
(19)
Запишем уравнение (17) в проекциях на оси x, y, z:
Вx = В1 + ВЕС + ВCD + BDЕ; (20)
В у
= 0;
(21)
у
= 0;
(21)
Вz = 0. (22)
Для определения магнитной индукции ВCD выполним вспомогательный чертеж (рис. 10) и получим:
![]() (23)
(23)
Из рис. 9 и 10 видно, что
1 = 30; 2 = 150,

Точка А расположена симметрично относительно одинаковых проводников EC, CD и DE, поэтому согласно формуле (23) индукции магнитных полей, созданных этими проводниками, будут равны, т. е. ВЕС = ВCD = BDЕ.
Вследствие этого формулу (22) можно переписать в виде:
Вx = В1 + 3ВCD. (24)
Магнитную индукцию В1 найдем по формуле:
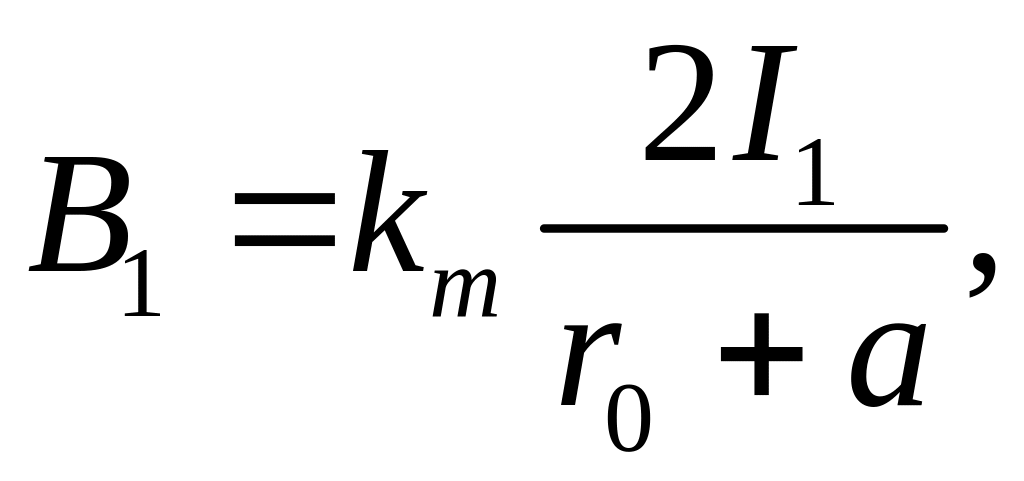 (25)
(25)
где
 ,
так как в точке А высота в равностороннем
треугольнике делится в соотношении 2:1
,
так как в точке А высота в равностороннем
треугольнике делится в соотношении 2:1
Подставив формулы (24) и (25) в уравнение (23), получим:
 (26)
(26)

 (27)
(27)
Подставив данные задачи в расчетную формулу (27), вычислим величину магнитной индукции в точке А:
 (Тл).
(Тл).
Значение вектора магнитной индукции совпадает со значением проекции Вх.
Ответ: В = 40 мкТл. Проекции вектора имеют следующие значения: = {40 мкТл; 0; 0}. Направление вектора совпадает с осью х, которая расположена перпендикулярно плоскости рис. 9.

 И
И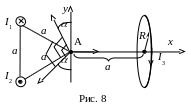 ешение.
ешение. ешение.
ешение.