2.6. Вычисления концентрации и активности ионов водорода и рН в растворах сильных электролитов

Теория сильных электролитов предложена в 1923 г. Дебаем и Хюккелем. Она успешно развивалась советскими химиками В.К. Семенченко, А.И. Бродским и др. В основе ее лежит учение об активности и ионной силе раствора (см. п. 1). Сильные электролиты в растворах ионизованы практически полностью. Современные физико-химические методы исследования не обнаруживают в растворах сильных электролитов недиссоциированных молекул. Истинная степень электролитической ионизации  = 100%. Экспериментальные исследования дают кажущуюся степень электролитической ионизации, которая часто значительно меньше 100%. Кажущейся степенью электролитической ионизации называют ту величину, которую дает непосредственное ее измерение с помощью физико-химических приборов. К сильным относят электролиты, кажущаяся степень ионизации которых больше 30%.

К сильным кислотам относятся HCl, НВr, НJ, H₂SO₄, HNO₃, HClO₄, HClO₃. Для одноосновной кислоты, процесс ионизации запишется уравнением:

НАn  Н⁺ + Аn^-

Концентрация ионов водорода [H⁺] = С_HAn (концентрация кислоты, моль/л), а активность ионов водорода: .

Показатель активности ионов водорода р_аН равен:

Для разбавленных растворов:

Если известна кажущаяся степень ионизации, то:

В общем случае для более строгих расчетов следует использовать следующий алгоритм:

1) вычислить ионную силу раствора  (II.1), (состав всех компонентов раствора должен быть известен);

2) вычислить по формуле (II.3) или взять из таблицы V (Приложение) коэффициент активности ионов водорода (при необходимости воспользоваться методом интерполяции, разобран в задаче №3, п.7);

3) вычислить активность ионов водорода: (моль/л);

4) вычислить раствора: .

Все случаи вычислений рассмотрены в п.7. В зависимости от необходимой точности вычислений расчеты проводят с учетом или без учета величин коэффициентов активности.

2.7. Решение типовых задач

Задача 1. Вычислить ионную силу раствора, содержащего в 1 л 0,02 моль NaNO₃ и 0,001 моль сульфата алюминия.

Решение. Обе соли, являются сильными электролитами и в растворе ионизованы полностью: NaNO₃  Na⁺ + NO₃^-

Al₂(SO₄)₃  2Al³⁺ + 3SO₄^2-

Ионная сила раствора вычисляется по формуле:

Концентрация всех присутствующих в растворе ионов соответственно равны: [Nа⁺] = 0,02 моль/л; [NO₃^-] = 0,02 моль/л; [Al³⁺] = 0,0012 = 0,002 моль/л; [SO₄^2-] = 0,0013 = 0,003 моль/л.

Подставив полученные значения концентраций ионов и их заряды в формулу для расчета , получаем:

 =1/2(0,021² + 0,021² + 0,0023² + 0,0032²) = 0,035.

Задача 2. Вычислить коэффициент активности и активность ионов Cl^- в 0,01 М растворе хлорида калия.

Решение. Хлорид калия как сильный электролит ионизирует на ионы полностью KCl = К⁺ + Cl^-.

1. Вычисляем ионную силу раствора :

 =1/2([K⁺]1² + [Cl^-]1² = 1/2(0,011² + 0,011²) = 0,01.

2. По таблице V (Приложение) находим коэффициент активности однозарядных ионов при  = 0,01:

3. Активность ионов хлора в данном растворе равна:

моль/л.

Задача 3. Вычислить коэффициенты активности ионов алюминия, если ионная сила раствора равна 0,035 (см. задачу №1).

Решение. В таблице V такое значение ионной силы раствора отсутствует. В этом случае можно провести вычисление по формуле (II.3) или воспользоваться приемом интерполяции. Рассмотрим этот прием. Из таблицы V выбираем интервал , включающий в себя  = 0,035 и соответствующе граничным значениям  этого интервала коэффициенты активности для 3-х зарядных ионов (Al³⁺):

				fAl3+
 1=0,01	0 ,025		f1	0 ,32
	0,035 =0,025			f	fAl3+=0,08
2=0,015	0,05		f2	0,24

 = 0,05 - 0,025 = 0,025;

f = 0,32 – 0,24 = 0,08;

a) f = 0,32 - f₁

;

f = 0,32 – 0,03 = 0,29.

При ионной силе раствора  = 0,035 коэффициент активности ионов алюминия равен 0,29. Это же значение коэффициента активности можно получить из второй части интервала, найдя f₂:

б) f = 0,24 + f₂;

f = 0,24 – 0,05 = 0,29.

Задача 4. Вычислить рН раствора, концентрация водородных ионов которого равна 0,002 моль/л.

Решение: рН = - lg[Н⁺];

рН = -lg0,002 = -lg(210^-3) = -lg2 –lg10^-3 = 3 - 0,30 = 2,7.

Задача 5. Вычислить [Н⁺] и [OН^-] в растворе, рН которого равен 4 (температура раствора 25°С).

Решение: [Н⁺] = 10^-4 моль/л; (моль/л)

Задача 6. Вычислить рН раствора соляной кислоты, концентрация которой 0,001 моль/л.

Решение: Соляная кислота как сильный электролит в растворе ионизирует полностью по схеме: НCl = Н⁺ + Cl^-. Находим ионную силу раствора:

 =1/2([Н⁺]1² + [Cl^-]1² = 1/2(0,0011² + 0,0011²) = 0,001.

При ионной силе  = 0,001 коэффициент активности ионов водорода = 0,97, активность ионов водорода

= 0,9710^-3 = 9,710^-4 моль/л;

Без учета ионной силы раствора [Н⁺] = C_HCl = 0,001 (10^-3) моль/л 

рН = -lg10^-3 = 3,0.

В данном случае, если не предусматривается точность расчетов до сотых долей, расчет можно проводить без учета ионной силы раствора, т.к. она достаточно мала.

Задача 7. Вычислить рН 0,02 M раствора синильной кислоты.

Решение. Синильная кислота как слабый электролит ионизирует по схеме: HCN  Н⁺ + CN^-.

Вычисления проводим по формуле (II.9):

По таблице 1 находим силовой показатель, рК = 9,3.

pH = 1/2  9,3 - 1/2lg(210^-2) = 4,65 - 1/2(0,30-2) = 4,65 + 0,85 = 5,5

Ответ: pH = 5,5.

Задача 8. Вычислить концентрацию гидроксид-ионов, ионов водорода и рН 0,01 М раствора гидроксида аммония при температуре раствора 50°С.

Решение. Гидроксид аммония, слабый электролит, в растворе ионизирует по схеме: NH₄ОH = NH₄⁺ + ОН^-.

Константа ионизации (табл. 1 Приложения).

Концентрацию гидроксид-ионов можно вычислить по формуле (II. 10)

По таблице VI находим значение ионного произведения воды при 50 ^оС: K_w = 5,510^-14

Находим рН раствора:

Задача 9. Вычислить концентрацию ионов водорода и рН 0,001 М раствора муравьиной кислоты.

Решение. Муравьиная кислота ионизирует по схеме:

НСООН  Н⁺ + НСОО^-

Константа ионизации K_НСООН = 1,810^-4; pK = 3,75. В этом случае первоначально вычисления проведем по формуле (II.7, § 5)

т.к. концентрация ионов водорода - величина положительная, то:

рН = -lg (3,4310^-4) = 4 - 0,54 = 3,46.

Для сравнения вычислим рН по упрощенной формуле (II.9, § 5)

рН = 1/23,75 - 1/2lg10^-3 = 1,875 + 1,5 = 3,375  3,38.

Разность в 0,08 (3,46 - 3,38) для приближенных расчетов невелика, и вычисления можно проводить по упрощенной формуле (II.9, § 5).

Задача 10. Вычислить концентрацию ионов водорода в 0,001 М растворе сероводородной кислоты.

Решение. Сероводородная кислота ионизирует в две ступени:

H₂S  Н⁺ + НS^- (1-я ступень)

HS^-  H⁺ + S^2- (2-я ступень)

Но таблице 1 находим константы ионизации:

Т.к.  , то концентрация ионов водорода в растворе, в основном, определяется ионизацией по первой ступени и вычисления можно провести по упрощенной формуле (II. 8):

;

моль/л.

Задача 11. Вычислить р_аН 0,1 М раствора гидроксида натрия при температуре раствора 80°С.

Решение. Гидроксид натрия - сильный электролит и в растворе ионизирует полностью: NaOH  Na⁺ + ОН^-.

Вычисляем ионную силу раствора:  = 1/2(0,11²0,11²) = 0,1.

При этой ионной силе  = 0,1,

(моль/л)

Вычислим активность ионов водорода, учитывая (табл. VI), что при 80°С ионное произведение воды К_w = 25,110^-14.

Задача 12. При какой концентрации уксусная кислота ионизована на 3%?

Решение. Уксусная кислота, как слабый электролит, ионизирует по схеме: CH₃CООH  CH₃CОО^- + Н⁺.

Пусть х моль/л - исходная концентрация кислоты, тогда [Н⁺] = [CH₃COO^-] = 0,03х моль/л, а равновесная концентрация кислоты [CH₃COOН] = 0,97x моль/л. Подставив полученные значения в выражение для константы ионизации, получим:

;

;

9,278х = 1,7410^-5 х = 1,8810^-6 моль/л.

Задача 13. Вычислить, как изменится степень ионизации уксусной кислоты при разбавлении раствора в 4 раза.

Решение. Запишем уравнение, связывающее степень ионизации с концентрацией слабого электролита (II.5):

;

Т.к. (по условию), то

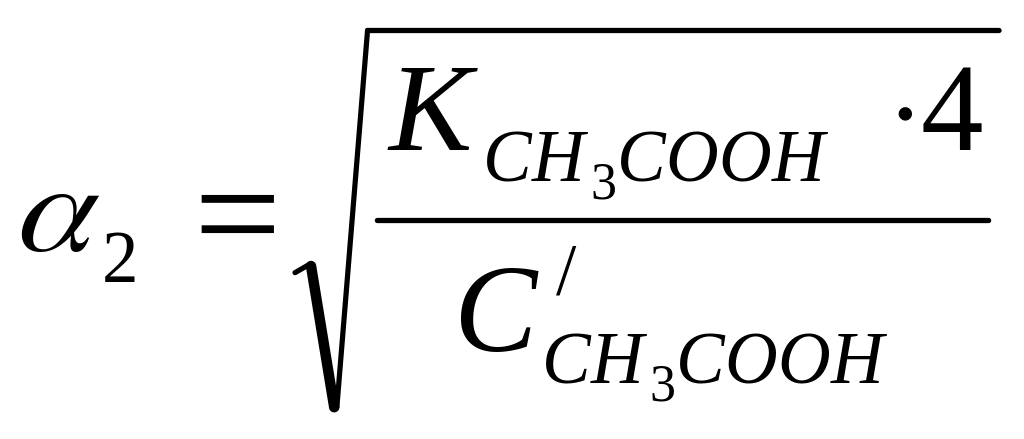
Степень ионизации возрастает в 2 раза.