Лабораторная работа № 4 двойственная задача

Текст задания: на основе решения двойственной задачи найти решение исходной (задача лабораторной работы № 3).

Ход работы

1. Записать математическую модель исходной задачи.

2. Записать математическую модель задачи двойственной исходной.

3. Записать математическую модель двойственной задачи в канонической форме

4. Загрузить приложение Лин_прогр.exe.

5. Ввести в программу исходные данные и, используя симплексный метод, получить решение задачи. Сформировать файл отчета.

6. Открыть файл отчета c помощью программы Microsoft Excel, оформить и распечатать файл отчета.

7. На основе решения двойственной задачи записать решение исходной задачи.

Содержание отчета

1. Текст задания.

2. Математическая модель исходной задачи.

3. Математическую модель задачи, двойственной исходной.

4. Математическую модель двойственной задачи в канонической форме.

5. Симплекс-таблица решения двойственной задачи.

6. Результаты решения задачи.

7. Проверка выполнения условий-ограничений двойственной задачи для найденного решения.

8. Решение исходной задачи.

9. Проверка выполнения условий-ограничений исходной задачи для найденного решения.

10. Дать экономическую интерпретацию переменных двойственной задачи.

Вопросы для подготовки

1. В чем заключается сущность двойственности в линейном программировании?

2. Пусть исходная задача состоит в оптимальном использовании ресурсов. Дайте экономическую интерпретацию двойственной задачи.

3. Поясните экономический смысл переменных задачи, двойственной задаче распределения ресурсов.

4. Правила формирования задачи (целевой функции и ограничений), двойственной исходной.

5. Как по решению двойственной задачи найти решение исходной задачи?

6. Как по решению исходной задачи найти решение двойственной задачи?

7. Сформулируйте теорему двойственности и следствия из нее.

8. Сформулируйте теорему о дополнительной нежесткости.

9. Что такое скрытый доход и теневая цена ресурса?

10. О чем говорит положительная двойственная оценка продукции?

Лабораторная работа № 5 параметрический анализ оптимального решения злп

Текст задания: средствами табличного процессора Microsoft Excel провести параметрический анализ решения задачи лабораторной работы № 3.

Под параметрическим анализом понимается решение задачи оптимизации для различных значений параметра (например, объем дефицитного ресурса), который ограничивает улучшение целевой функции.

Ход работы

1. Записать математическую модель исходной задачи.

2. Ввести математическую модель задачи табличный процессор Microsoft Excel.

3. Получить решение задачи и определить из него лимитирующие (дефицитные) ресурсы.

4. Получить решение задачи для объемов дефицитного ресурса ±20 % и ±40 % исходного значения.

Порядок выполнения параметрических расчетов.

1. Выбрать лимитирующее ограничение (например, ресурс, который является дефицитным) и задаться некоторыми значениями его правой части (размером ресурса)

2. Получить оптимальное решение задачи для каждого значения лимитирующего ресурса и поместить результаты в таблицу (табл. 5-1). Для удобства проведения параметрического анализа отформатируйте содержимое ячеек таким образом, чтобы дробная часть содержала не более двух знаков после десятичной точки.

3. Построить гистограммы дохода (прибыли, расхода), продукции и расхода ресурсов в зависимости от правой части лимитирующего ограничения.

В качестве примера рассмотрим задачу об определении оптимальных объемов выпуска продукции, рассмотренную в лабораторной работе № 3. Одним из лимитирующих ресурсов в этой задаче являлся Материал М2. Поэтому получим оптимальные решения задачи для различных значений объемов ресурса «Материал М2»: 240, 270, 300, 330, 360.

Таблица 5-1

Результаты параметрического анализа

Вариант	1	2	3	4	5
Материал М2	240	270	300	330	360
Р1(х1)	0	0	0	0	0
Р2(х2)	70	70	70	100	100
Р3(х3)	170	200	230	230	230
ЦФ	99000	114000	129000	135000	135000
ВР станка С1, минуты	310	340	370	430	430
ВР станка С2, минуты	340	400	460	460	460
Материал Ml, фунты	280	280	280	400	400
Материал М2, фунты	240	270	300	330	330

Получим оптимальное решение задачи для каждого значения (ячейка G11) лимитирующего ресурса «Материал М2». Результаты моделирования поместим в таблицу 5-1 и построим гистограммы, которые позволяют оценить управленческое решение по параметру «Материал М2»: ожидаемый доход (рис. 5-1), номенклатуру и объемы выпускаемой продукции (рис. 5-2), объем используемого сырья (рис. 5-3).

Анализ результатов параметрического моделирования следует увязать с отчетом по устойчивости (рис. 3-8). В соответствии с отчетом по устойчивости базисное решение, теневые цены ресурсов и нормированная стоимость продукции не изменятся, если объем ресурса «Материал М2» будет лежать в пределах 70-300 фунтов, а его теневая цена (скрытый доход) в этом диапазоне будет составлять 500$, т.е. увеличение (уменьшение) размера ресурса «Материал М2» на 1 минуту дает дополнительную прибыль (снижение прибыли) 500$.

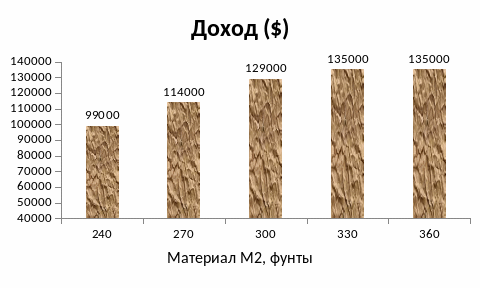
Рис. 5-1

Поэтому снижение объема ресурса «Материал М2» с 300 фунтов до 270 фунтов и с 270 фунтов до 240 фунтов приводит каждый раз к уменьшению дохода на 500$*30 = 15000$ (129000-15000=114000 и 114000-15000=99000).

При объеме ресурса «Материал М2» свыше 300 мин. меняются базисное решение и нормированная стоимость продукции: становится выгодным производство продукции Р2 (рис. 5-2). Так как доход от продукции Р2 ниже, чем от продукции Р3, то доход фирмы при увеличении объема ресурса «Материал М2» с 300 фунтов до 330 фунтов растет на 6000$. Дальнейший рост объема ресурса «Материал М2» не дает дополнительного дохода, так как полностью использованы ресурсы «Время работы станка С2» и «Материал Ml» (рис. 5-3).

Рис. 5-2

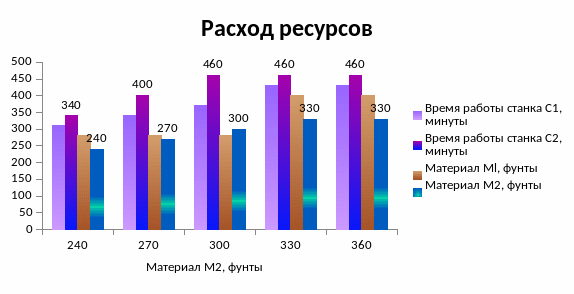
Рис. 5-3

Содержание отчета

1. Текст задачи.

2. Математическая модель исходной задачи и ее решение.

3. Результаты решения задачи для объемов лимитирующих ресурсов.

4. Гистограммы: целевая функция – объем лимитирующего ресурса, расходы ресурсов – объем лимитирующего ресурса, выпуск продукции – объем лимитирующего ресурса.

5. Экономическая интерпретация полученных результатов.

Вопросы для подготовки

1. В чем заключается сущность параметрического анализа?

2. Пусть исходная задача состоит в оптимальном использовании ресурсов. Дайте экономическую интерпретацию двойственной задачи.

3. Поясните экономический смысл переменных задачи, двойственной задаче