Создание формы для ввода условий задачи.
Весь текст, введенный на форме, является комментарием и на решение задачи не влияет. Введите исходные данные в форму (рис. 3-1).
Рис. 3-1
Правая часть выражения целевой функции (значение целевой функции) записывается в ячейку Е5 и определяется как сумма произведений значений ресурсов (ячейки с В2 до D2) на соответствующие коэффициенты целевой функции (ячейки с В5 по D5), т.е. формула для расчета содержимого ячейки E5 примет вид: =СУММПРОИЗВ(B2:D2;B5:D5). Ввод зависимости осуществляется через окно Мастер функций.
По аналогичным зависимостям вычисляются левые части уравнений-ограничений. Для формирования их можно воспользоваться копированием. С этой целью нужно отредактировать формулу в Е5 следующим образом: =СУММПРОИЗВ(B$2:D$2;B5:D5) и скопировать содержимое в E8, E9, E10, E11.
Формирование ограничений производится с помощью диалогового окна «Поиск решения». Для его вызова нужно выбрать команду Поиск решения из меню Сервис.
Затем нужно выполнить следующие действия:
– в окне Установить целевую ячейку ввести адрес E5 (либо путем набора, либо путем помещения курсора в ячейку E5);
– ввести направление целевой функции: максимальному значению;
– ввести адреса искомых ячеек В2-D2 в поле Изменяя ячейки (или поместить курсор в поле Изменяя ячейки и пометить ячейки В2-D2);
Рис. 3-2
– нажать кнопку Добавить и в открывшемся окне Добавление ограничения ввести граничные условия (рис. 3-3).
Рис. 3-3. Пример ввода ограничения на основные переменные
После ввода последнего ограничения вместо Добавить нажать кнопку OК. На этом ввод условий задачи заканчивается.
Решение задачи
В окне Поиск решения нажать кнопку Параметры. После этого на экране появится окно Параметры поиска решения (рис. 3-4).
Рис. 3-4
С помощью команд, находящихся в этом диалоговом окне, можно вводить условия для решения ряда задач оптимизации.
Параметры:
– максимальное время – время в секундах, выделяемое для решения задачи (до 9 часов);
– предельное число итераций (100 – подходит для решения практически всех задач, решаемых средствами Excel).
Решение задачи начинаем с установки флажка Линейная модель и нажатия кнопки ОК.
После нажатия в окне Поиск решения кнопки Выполнить появляется окно Результаты поиска решения.
Возможны три варианта решения ЗЛП и соответствующих им вариантов выдаваемых в окне сообщений:
– Решение найдено. Все ограничения и условия оптимальности выполнены (рис. 3-5);
Рис. 3-5
– условия задачи несовместны (Сообщение – Поиск не может найти подходящего решения);
– целевая функция не ограничена (Сообщение – Значения целевой ячейки не сходятся).
Найденное решение помещается в строке 2 таблицы условий задачи (рис. 3-6).
Рис. 3-6
Анализ оптимального решения
Для проведения анализа решения можно из окна Результаты решения можно вызвать отчеты трех типов:
– в отчете Результаты выводятся исходные и полученные в результате поиска решения значения изменяемых ячеек (переменных задачи) и целевой функции, а также сведения об ограничениях задачи;
– отчет Устойчивость дает основную информацию для анализа чувствительности найденного оптимального решения к небольшим изменениям параметров модели;
– в отчете Пределы показаны наименьшее и наибольшее пределы значения, которые может принимать каждая изменяемая переменная целевая функция.
Для вызова отчета маркер устанавливается на соответствующий вид отчета, а затем нажимается кнопка Ok.
Отчет по результатам (рис.3-7) состоит из трех таблиц.
Таблица Целевая ячейка содержит сведения о начальном и оптимальном значении целевой функции.
Таблица Изменяемые ячейки включает начальные и оптимальные значения искомых переменных, полученных в результате решения задачи;
Таблица Ограничения показывает сведения только о тех ограничениях, которые отображаются в списке Ограничения диалогового окна Поиск решения:
– адреса ячеек, на значения которых наложены ограничения;
– их имена (составленные из заголовков строк и столбцов, на пересечении которых находятся изменяемые ячейки); если имен нет, то это поле остается пустым;
– значение в этих ячейках после получения оптимального решения (величины использованных ресурсов);
– формула ограничения;
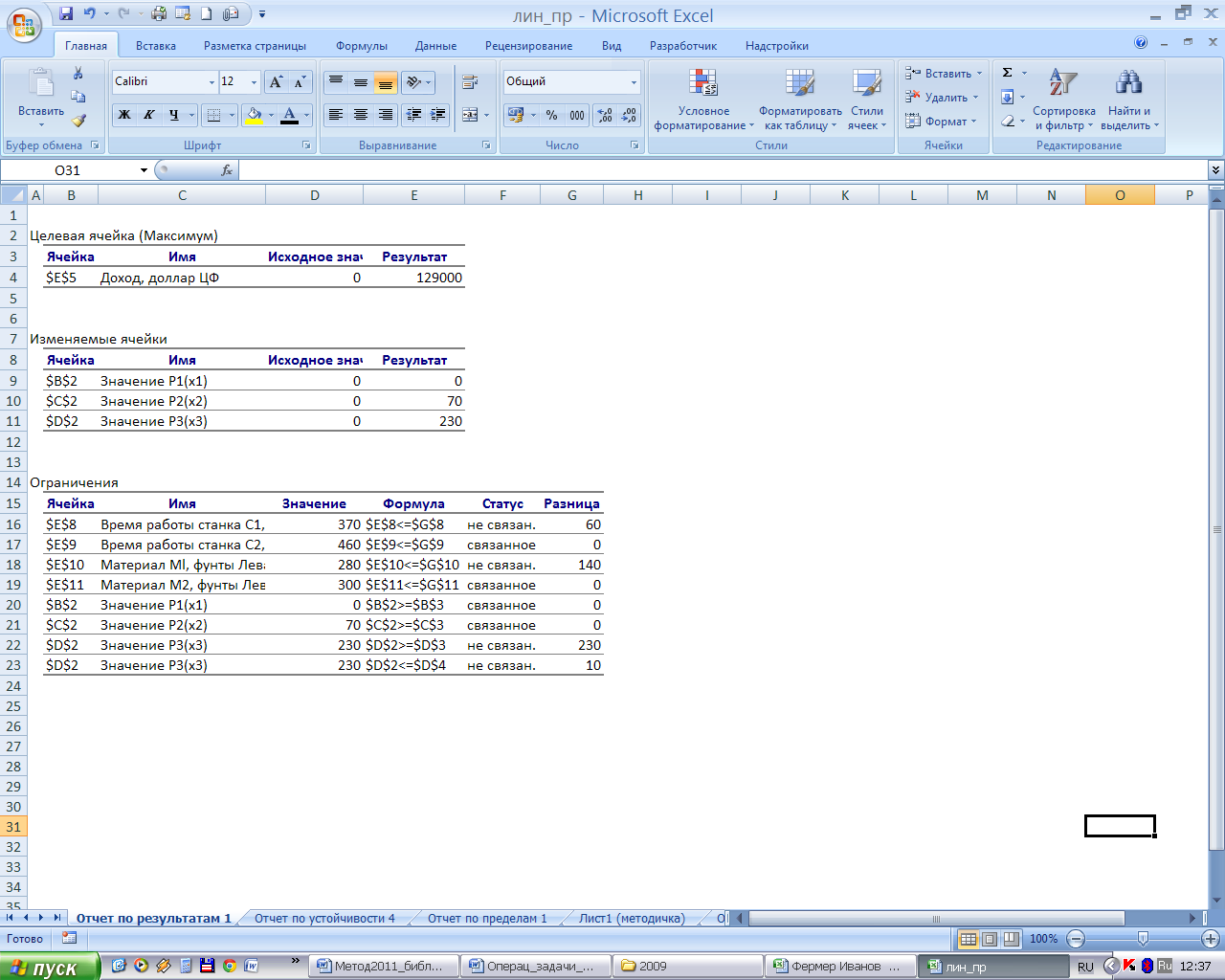
Рис. 3-7
– статус ограничения «связанное», если в оптимальном решении ограничение выполняется как равенство и «не связан.», если ограничение выполняется как неравенство. Ограничение получает статус «связанный», если ресурс дефицитный или переменная приняла нижнее предельное значение (продукция не выгодна), «несвязанный», если ресурс недефицитный или переменная приняла ненулевое значение (продукция выгодна);
– разница – объем неиспользованных ресурсов.
В нашем примере ресурсы «время работы станка С1» и «материал М2» имеют статус «не связан.», то есть находятся в избытке. Ресурсы «время работы станка С2» и «материал М1» имеют статус «связанное», то есть израсходованы полностью и сдерживают увеличение дохода. Переменные Р1 и Р2 приняли нижние предельные значения соответственно 0 и 70, то есть производство этих видов продукции не выгодно. Производство продукции Р3 выгодно, она получила статус «не связан.». Если объем дефицитных ресурсов увеличится, то производство продукции Р3 может достигнуть максимального значения (240 единиц).
Отчет по устойчивости состоит из двух таблиц (рис. 3-8).
Рис. 3-8
В таблице Изменяемые ячейки:
– графа «Нормированная стоимость» содержатся двойственные оценки продукции со знаком «-», показывающие, насколько изменится (уменьшится) значение целевой функции, если на единицу изменится значение в данной изменяемой ячейке. Выгодная продукция имеет нулевые двойственные оценки, невыгодная отрицательные (чем ниже нормированная стоимость продукции, тем менее она выгодна);
– приводятся интервалы устойчивости коэффициентов целевой функции (столбцы Допустимое увеличение и Допустимое уменьшение).
При имеющихся объемах ресурсов производство продукции Р1 и Р2 является невыгодным и может стать выгодным лишь при возрастании дохода для Р1 до 500$ (Целевой коэффициент + допустимое увеличение или Целевой коэффициент – нормированная стоимость), для Р2 – до 500$. Прибыль от реализации продукции Р3 может меняться в пределах от 300$ (500-200) до ∞ (от 60-12 до 60+40). При выходе коэффициентов ЦФ за указанные пределы может измениться номенклатура выпускаемой продукции или поменяться статус ресурсов.
В таблице Ограничения приведены:
– интервалы устойчивости ресурсов – возможный диапазон изменения объемов ресурсов (столбцы Допустимое увеличение и Допустимое уменьшение). При выходе объемов ресурсов за указанные пределы может измениться номенклатура выпускаемой продукции или поменяться статус ресурсов;
– теневая цена ресурса показывает, насколько изменится значение целевой функции, если на единицу изменится значение правой части данного ограничения; теневая цена отлична от нуля только тогда, когда данное ограничение в оптимальном решении является связанным, т.е ресурс является дефицитным (и решение не вырождено).
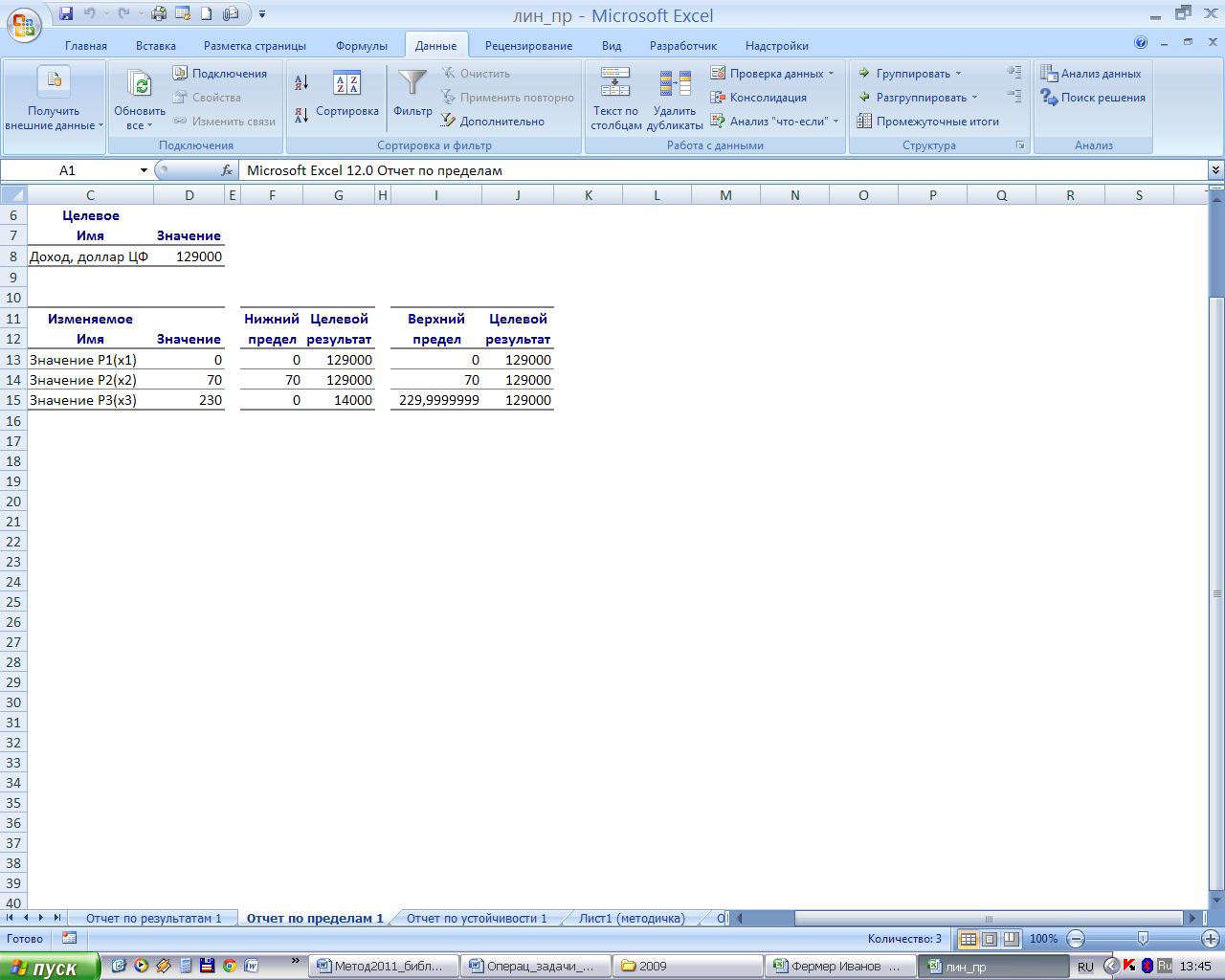
Рис. 3-9
Отчет по пределам (рис. 3-9) показывает, в каких пределах может быть изменен выпуск продукции, вошедшей в оптимальное решение, при сохранении структуры оптимального решения:
– приводятся значения переменных в оптимальном решении;
– приводятся нижние пределы изменения переменных, если на значение переменной не налагаются ограничения, задающие ее верхнюю (или нижнюю) границу, то в соответствующих столбцах для этой переменной будут стоять значения ошибки #Н\Д.
– в графе G указаны значения целевой функции при выпуске данного типа продукции на нижнем пределе (при Р3(х3) = 0) F = 200*70 + 500*0= 14000, в графе J – на верхнем пределе (везде 129000).
Содержание отчета
Текст задачи.
Представление задачи в виде таблицы.
Математическая модель задачи.
Математическая модель задачи в канонической форме.
Симплекс-таблица решения задачи.
Результаты решения задачи.
Проверка выполнения условий-ограничений.
Симплекс-таблица решения задачи на последнем шаге итерации.
Влияние на оптимальное решение вклада переменных в прибыль (коэффициентов в выражении целевой функции):
– коэффициентов при небазисных переменных в исходном выражении целевой функции;
– коэффициентов при базисных переменных в исходном выражении целевой функции.
Дать экономическую интерпретацию полученных результатов.
10. Влияние констант в правых частях ограничений:
– приращения в правой части ограничения, из которого в окончательный базис вошла свободная переменная;
– приращения в правой части ограничения, из которого в окончательный базис вошла основная переменная.
Дать экономическую интерпретацию полученных результатов.
Сравните результаты анализа результатов решения задачи обоими способами.