Однородные уравнения первого порядка

Прежде чем перейти к рассмотрению вопроса о решении однородных уравнений первого порядка познакомимся с понятием однородных функции.

Определение 1. Функция называется однородной функцией -го измерения относительно переменных и , если при любом справедливо тождество

.

Так, например, функция однородная функция первого измерения, т.к. ;

функция однородная функция нулевого измерения, т.к. ;

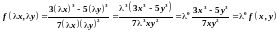функция не однородная функция, т.к. однородная функция первого измерения, а однородная функция четвёртого измерения.

Определение 2. Уравнение первого порядка называется однородным относительно и , если функция есть однородная функция нулевого измерения относительно и .

Однородные уравнения первого порядка приводятся к уравнениям с разделяющимися переменными с помощью подстановки

Уравнение вида будет однородным тогда и только тогда, когда функции и будут однородными функциями одного и того же измерения.

Например, однородное уравнение;

не однородное уравнение.

Замечание: Уравнения вида при приводятся к однородным подстановкой где точка пересечения прямых и Таким образом, для определения и необходимо решить систему уравнений:

Если же , то подстановка позволяет разделить переменные.

Линейные уравнения первого порядка

Определение. Линейным уравнением первого порядка называется уравнение, линейное относительно неизвестной функции и её производной.

Линейное уравнение первого порядка имеет вид:

(1)

где заданные непрерывные функции от или постоянные числа.

Решение линейного уравнения будем искать в виде произведения двух функции от :

(2)

где . Дифференцируя обе части последнего выражения, получим:

(3)

Значения подставим в данное уравнение (1)

или

Выберем функцию такой, чтобы

, (4)

тогда . (5)

Решив сначала уравнение (4) и затем уравнение (5), найдём значения и . Подставив значения и в (2) найдём решение уравнения (1).

Замечание: Уравнение вида , (6)

где и , называется уравнением Бернулли.

Уравнение Бернулли приводится к линейному следующим преобразованием: разделим все члены уравнения на

(7)

и произведём замену . (8)

Тогда . (9)

Подставив значения (8) и (9) в (7), получим или

(10)

Решив линейное уравнение (10) и учитывая, что , найдём решение уравнения (6).

_{Заметим, что уравнение (6) часто можно решить как и линейное уравнение с пом}ощью подстановки

Уравнение в полных дифференциалах

Определение. Уравнение

называется уравнением в полных дифференциалах, если и - непрерывные, дифференцируемые функции, для которых выполняется соотношение

Левая часть такого уравнения есть полный дифференциал некоторой функции . Если это уравнение переписать в виде , то его общее решение определяется равенством Функция может быть найдена по формуле

.