2. Программная модель сопроцессора

С точки зрения программиста, сопроцессор представляет собой совокупность регистров, каждый из которых имеет свое функциональное назначение (рис. 3.1).

В программной модели сопроцессора можно выделить три группы регистров.

1) Восемь регистров r 0 . . . r 7, составляющих основу программной модели сопроцессора — стек сопроцессора. Размерность каждого регистра 80 битов. Такая организация характерна для устройств, специализирующихся на обработке вычислительных алгоритмов. Вычисление выражения заключается в выборке с вершины стека очередной операции. Если это двухместная операция, то с вершины стека снимаются два операнда, над которыми и производятся действия в соответствии со снятой ранее операцией. Реализация численных алгоритмов на основе регистрового стека позволяет получить существенный выигрыш в скорости вычислений.

2) Три служебных регистра:

- регистр состояния сопроцессора swr — отражает информацию о текущем состоянии сопроцессора. В регистре swr содержатся поля, позволяющие определить: какой регистр является текущей вершиной стека сопроцессора, какие исключения возникли после выполнения последней команды, каковы особенности выполнения последней команды (некий аналог регистра флагов основного процессора) и т. д.;

- управляющий регистр сопроцессора cwr — управляет режимами работы сопроцессора. С помощью полей в этом регистре можно регулировать точность выполнения вычислений, управлять округлением, маскировать исключения;

- регистр слова тегов twr — используется для контроля за состоянием каждого из регистров r0 . . . r7. Команды сопроцессора используют этот регистр, например, для того, чтобы определить возможность записи значений в эти регистры.

3) Два регистра указателей — данных dpr и команд ipr. Они предназначены для запоминания информации об адресе команды, вызвавшей исключительную ситуацию и адресе ее операнда. Эти указатели используются при обработке исключительных ситуаций (но не для всех команд).

Все эти регистры являются программно доступными. Однако к одним из них доступ получить достаточно легко, для этого в системе команд сопроцессора существуют специальные команды. К другим регистрам получить доступ сложнее, так как специальных команд для этого нет, поэтому необходимо выполнить дополнительные действия.

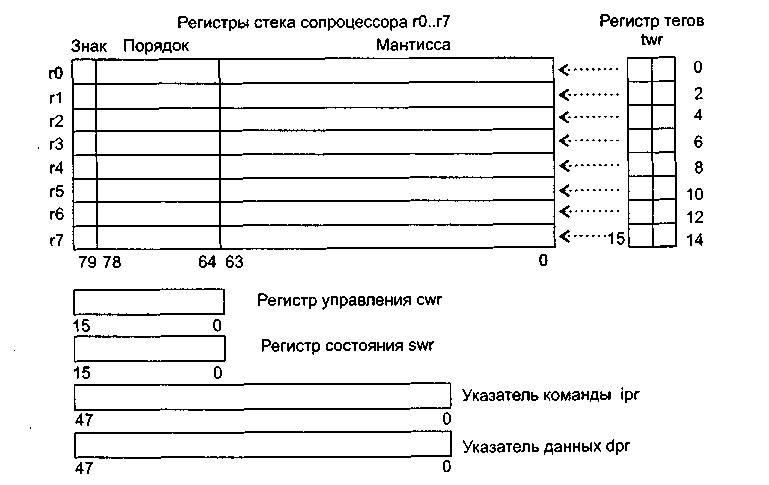
Рисунок 3.1 - Программная модель сопроцессора

3. Форматы представления вещественных чисел

Для изображения чисел c плавающей точкой в сопроцессоре существует три формата данных. Короткий формат имеет 32 бита, а длинный 64 бита. Третий формат определяет 80-битовые числа. Сопроцессор использует такой формат "промежуточного действительного числа", чтобы обеспечить очень высокую точность для промежуточных результатов вычислений.

Целые числа — лучший способ представления многих величин. Целые числа просто понимать и использовать, а также легко преобразовывать в двоичное представление. Однако c целыми числами плохо работать в случае очень больших значений. Очень большое целое число обычно оканчивается длинной строкой нулей, например, Солнце находится на расстоянии около 93 000 000 миль от Земли. Целые числа, кроме того, не способны представить значение, содержащее дробную часть, т. e. ЭВМ не может запомнить число 1/2 в целом представлении. Любые другие дроби, меньше 1, также невозможно представить, используя целые числа.

Ученые и математики давным-давно разработали способ представления этих чисел в достаточно удобном виде. На первом этапе вводится десятичная точка (.), которая будет показывать границу между целой и дробной частями числа. В случае целого числа позиция, представляющая единицы, всегда находится на правом краю числа; в случае, когда используется десятичная точка, цифры справа от нее представляют значения, меньше 1.

У целых чисел каждая позиция числа соответствует степени числа 10, т. e. число 1234 есть

1234= 1000 + 200+30+4= 110³ +210² +310¹ +410⁰.

Десятичная точка показывает границу между позицией, соответствующей 10⁰, и дробной частью. В дробной части позиции снова являются степенями числа 10, но теперь эти степени - отрицательные. Поэтому число 1.234 есть

1.234+ 1 + 0.2 + 0.03 + 0.004= 110⁰ +210^-1 +310^-2 +410^-3.

Поскольку каждая позиция десятичного числа отличается от соседней на степень числа 10, умножение числа на 10 эквивалентно сдвигу десятичной точки на одну позицию вправо. Аналогично деление на 10 сдвигает десятичную точку на позицию влево. Это свойство можно использовать для сдвига десятичной точки на соответствующее место: мы сдвигаем десятичную точку и одновременно корректируем число на ту же степень числа 10. Такое представление чисел называется представлением c плавающей точкой, поскольку десятичная точка "плавает" в числе; она больше не помечает абсолютное место между целой и дробной частями. Положение десятичной точки можно выбрать из соображений удобства, а затем умножить число на нужную степень числа 10, чтобы получить правильное значение.

Десятичное число c плавающей точкой состоит из двух частей. Значащая часть числа называется мантиссой. На практике мантисса обычно находится в пределах 1 < мантисса < 10. Другая часть числа c плавающей точкой - это порядок, степень, в которую нужно возвести число 10 перед умножением его на мантиссу, т. e. 9.310⁷ имеет мантиссу 9.3 и порядок 7. Если основание системы счисления определено раз и навсегда, в нашем случае это 10, то для восстановления первоначального числа должны быть заданы только два числа — мантисса и порядок.

Двоичные числа c плавающей точкой изображаются аналогично десятичным; отличие заключается в том, что основание системы счисления здесь 2, а не 10. Мантисса имеет значения 1 < мантисса < 2, а порядок показывает степень числа 2

Для того чтобы сохранить максимальную точность, вычислительные машины почти всегда хранят мантиссу в нормализованном виде. Это означает, что мантисса есть число, лежащее между 1 и 2 (1 < мантисса < 2). Два соображения говорят в пользу нормализации. Во-первых, ни один незначащий 0 не дает никакого вклада в точность числа. (Это несправедливо для нулей, лежащих в конце числа; мы считаем, что число 1.000 более точно, чем число 1.0.) Если в мантиссе c плавающей точкой появились незначащие нули, точность числа падает. Во-вторых, способ хранения мантиссы числа c плавающей точкой подразумевает, что двоичная точка находится на фиксированном месте. Фактически подразумевается, что двоичная точка следует после первой двоичной цифры, т. e. нормализация мантиссы делает единичным первый бит, помещая тем самым значение мантиссы между 1 и 2. Для выполнения нормализации ЭВМ корректирует порядок числа на соответствующее значение.

Точно так же, как длина мантиссы числа определяет его точность, длина поля порядка определяет диапазон числа. Поле порядка содержит степень числа 2, и чем больше бит в этом поле, тем большее число может быть представлено.

Важно отметить, что, хотя диапазон и расширяется c увеличением числа бит порядка, точность не увеличивается. Значение порядка хранится не как число, представленное в дополнительном коде. Для упрощения вычислений значение порядка в ЭВМ хранится в виде смещенного числа. Это означает, что к действительному значению порядка прибавляется смещение перед записью его в память. Значение смещения выбрано так, чтобы допустить сравнение порядков. В частности, это полезно при сравнении двух чисел c плавающей точкой. Значения порядка и мантиссы записываются в одном элементе данных, причем порядок записывается перед мантиссой. В случае смещенного значения порядка программа может сравнивать числа побитно, начиная со старших позиций. Первое же неравенство показывает соотношение чисел, и больше не нужно учитывать никакие части чисел. Значение смещения определяется размером поля порядка. Более подробная информация о компьютерном представлении вещественных чисел, с которыми работает сопроцессор, имеется в [2].