Задания на Курсовую работу

по дисциплине «Информатика»

Составить блок-схему алгоритма и написаить программу на языке С++ для задачи в варианте, соответствующем номеру студента в журнале. Отчет должен содержать: постановку задаачи, математическую модель, описание метода решения, блок-схему алгоритма, программа на языке С++, пример решения задачи. Исходные данные должны браться из файла, а результат выводится на экран.

К отчету должен прилагаться CD (либо DVD) диск, содержащий файл отчета в формате MS Word, файлы с исходным текстом программы, исполняемый файл программы и файл с исходными данными.

Информацию по математической модели и методам решения можно найти на сайте www.mathserfer.com

Варианты заданий

Действия над матрицами

1 Транспонирование матрицы

2 Сложение матриц

3 Вычитание матриц

4 Умножение матриц

5 Умножение матрицы на число

6 Определитель (детерминант) матрицы

7 Обратная матрица

8 Ранг матрицы

Решение систем линейных уравнений

9 Методом Крамера

10 Методом обратных матриц

11 Методом Гаусса (Жордана-Гаусса)

Действия над векторами

12 Найти модуль (длину) вектора

13 Коллинеарны ли два вектора?

14 Ортогональность векторов (Перпендикулярны ли два вектора?)

15 Сложение, вычитание, скалярное произведение векторов

16 Векторное произведение векторов

17 Найти угол между векторами

18 Найти косинус угла между векторами AB и AC

19 Найти проекцию одного вектора на другой

20 Компланарны ли три вектора?

21 Разложить вектор по векторам (по базису)

Транспонирование матрицы

Над матрицами определена еще одна операция, называемая транспонированием.

        Определение 14.5   Пусть -- матрица размеров . Тогда транспонированной матрицей называется такая матрица размеров , что , , .         

Транспонированная матрица обозначается или . Операция транспонирования заключается в том, что строки и столбцы в исходной матрице меняются ролями. В транспонированной матрице первым столбцом служит первая строка исходной матрицы, вторым столбцом -- вторая строка исходной матрицы и т.д. Например,

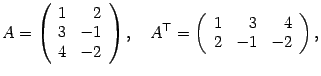
Читатель легко проверит, что

где -- число.

        Предложение 14.5   Если произведение определено, то

(14.8)

        Доказательство.     Пусть -- матрица размеров ,  -- матрица размеров . Тогда имеет размеры ,  -- размеры . Число столбцов в совпадает с числом строк в , поэтому произведение на определено. Размеры этого произведения . Матрица имеет размеры , поэтому  -- матрица размеров . Итак, матрицы в правой и левой части равенства (14.8) существуют и имеют одинаковые размеры.

Пусть , , , , . Нам нужно показать, что , , .

По определению транспонирования . По определению умножения матриц

(14.9)

С другой стороны,

Поэтому

Сравнивая полученный результат с (14.9), получаем .