Г лава 4

Допущения (1) множественные отказы и отказы других типов статистиче­ски независимы; (2) множественные отказы связаны с выходом из строя не менее двух элементов; (3) при отказе одного из нагруженных резервирован­ных элементов отказавший элемент восстанавливается, при отказе обоих элементов восстанавливается вся система; (4) интенсивность множествен­ных отказов и интенсивность восстановлений постоянны.

Обозначения

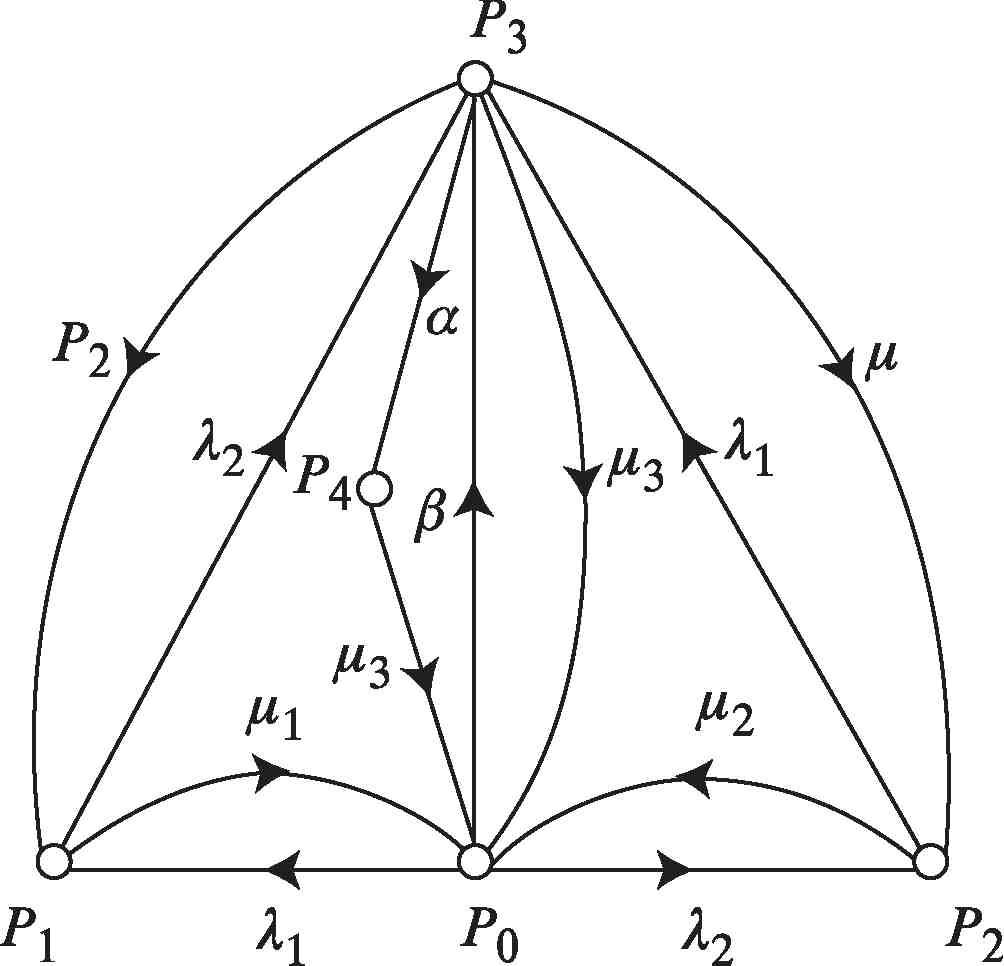
P0(t) — вероятность того, что в момент времени tоба элемента функцио­нируют;

P1(t) — вероятность того, что в момент времени t элемент 1 вышел из строя, а элемент 2 функционирует;

P2(t ) — вероятность того, что в момент времени t элемент 2 вышел из строя, а элемент 1 функционирует;

P ₃(t ) — вероятность того, что в момент времени t элементы 1 и 2 вышли из строя;

P4(t) — вероятность того, что в момент времени t имеются специалисты и запасные элементы для восстановления обоих элементов;

Xi — постоянная интенсивность отказов элементов 1 и 2 (i = 1, 2);

цi — постоянная интенсивность восстановлений элементов 1 и 2 (i = 1,2);

И3 — постоянная интенсивность восстановлений элементов 1 и 2;

а — постоянный коэффициент, характеризующий наличие специали­стов и запасных элементов;

(3 — постоянная интенсивность множественных отказов;

t — время.

Рассмотрим три возможных случая восстановления элементов при их одновременном отказе:

Случай 1. Запасные элементы, ремонтный инструмент и квалифициро­ванные специалисты имеются для восстановления обоих элементов, т. е. элементы могут быть восстановлены одновременно.

Случай 2. Запасные элементы, ремонтный инструмент и квалифициро­ванные специалисты имеются только для восстановления одного элемента, т. е. может быть восстановлен только один элемент.

Случай 3. Запасные элементы, ремонтный инструмент и квалифициро­ванные специалисты отсутствуют, и, кроме того, может существовать оче­редь на ремонтное обслуживание.

Математическая модель системы, изображенной на рис. 4.5.22, пред­ставляет собой следующую систему дифференциальных уравнений первого порядка:

178

Г ЛАВА 4

Рис. 4.5.22. Модель готовности системы в случае множественных отказов

(2 Л 3

(4.5.44)

P'i(0=-(A.2 +т)P0 + PК0ц2 + P№ь P'2 (0 = -ЧЯ-1 + Ц2 ) P (О + Pо (ОЯ-2 + P (От,

^ 3 Л 2

P'з (0 = J 2>i +а P₃(0 + 2P_i№(3-0 + Pо(ОР, i=1 у i=1

P'₄(0 = -цзP(0 + Pз(Оа.

При t = О имеем Pq(0) = 1, а другие вероятности равны нулю. Приравнивая в полученных уравнениях производные по времени нулю, для установившегося режима получаем:

2 3

2>i +р Po + LP_{i i}+Pw =0,

-(Я-2 +V\)P\+PW2 +PъХ\ =0,

-(М + Ц2 )P + P^2 + P W = 0,

(4.5.45)

f 3 Л 2

2> + а P + ZP_io-o + PР = о,

i=1 У i=1

-цз P + Pа = 0,

4

P_i-1=0.

i=о

Решая эту совместную систему уравнений, получаем:

179

Г ЛАВА 4

P₀

P

где 9 =

P₀ (P₁ / P₀)

_{л =m,}

P₂ P₃

М+Ц2 Ц2(М+Ц2)

^2 + Ц1 «(^2 + щ)

+

+

I L m(^2 + i-u)

+ Ц2

A4 a^i

I I

J

Ц2 (^1 + ^2 + Vl)

Ц2ЦЗ

+ 1 ,

J

L I

H

М+Ц2 (А-1+Ц2)Ц2 Ц2 Ц2ЦЗ

Ашз +aAi | U2^2 I I J-ilAi I I

Lm+mJ Ui+_mJ

| + | +Л-1 +Л-2 +p I x

J

L

M-2

Гцз(^2 + m) + a(^2 + ui) ш(Х2 + ш)

1 Ь Щ

M-2

L

(^1 +Ц2)

|ilAi

k2

P₀

М-2

М-2

|il(X₂ +щ)Л |i₂(Xi + ц₂)

(4.5.46)

(4.5.47)

_ аР\{%2 + ш) аХ\ _л "з = ^0 •

Ц2ЦЗ Ц2ЦЗ

Стационарный коэффициент готовности может быть вычислен по фор­муле:

К

2

i=0

180