7.5. Алгебраические операции над нечеткими множествами.

Алгебраическим произведением нечетких множеств и называется нечеткое множество, функция принадлежности которого определяется следующим образом:

(7.19)

Алгебраической суммой нечетких множеств и называется нечеткое множество, функция принадлежности которого определяется следующим образом:

(7.20)

Для операций выполняются свойства:

1. Коммутативный закон

(7.21)

2. Ассоциативный закон

(7.22)

3. Закон де Моргана

(7.23)

4. Операции с пустым множеством:

, (7.24)

5. Операции с универсумом:

(7.25)

Не выполняются следующие свойства:

1. Дистрибутивный закон

(7.26)

2. Закон идемпотентности

(7.27)

3. Закон исключенного третьего

(7.28)

На основе операции алгебраического произведения определяется операция возведения в степень нечеткого множества , где - положительное число. Нечеткое множество определяется функцией принадлежности:

(7.29)

Частным случаем возведения в степень являются операции концентрирования и растяжения , которые используются при работе с лингвистическими неопределенностями. Наглядное представление этих операций представлено на рис 7.9.

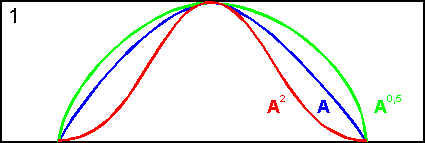
Рис. 7. 9.

Умножением на число , где - положительное число такое, что , называется нечеткое множество с функцией принадлежности:

(7.30)

Пусть даны нечеткие множества универсального множества и неотрицательные числа , сумма которых равна 1. Выпуклой комбинацией нечетких множеств называется нечеткое множество с функцией принадлежности :

(7.31)

Декартовым произведением нечетких множеств , каждое из которых является подмножеством соответствующего универсального множества , называется нечеткое множество, являющееся подмножеством универсального множества , с функцией принадлежности:

(7.32)

Оператор увеличения нечеткости используется для преобразования четких множеств в нечеткие и для увеличения нечеткости нечеткого множества.

Пусть - нечеткое множество, - универсальное множество и для всех определены нечеткие множества . Совокупность всех называется ядром оператора увеличения нечеткости Ф. Результатом действия оператора Ф на нечеткое множество A является нечеткое множество вида:

, (7.33)

где - произведение числа на нечеткое множество.

Пример

Тогда

8. Нечеткая логика.

Нечеткая логика это обобщение традиционной логики на случай, когда истинность рассматривается как лингвистическая переменная, принимающая значения типа: "очень истинно", "более-менее истинно", "не очень ложно" и т.п. Указанные лингвистические значения представляются нечеткими множествами.

8.1. Лингвистические переменные

Лингвистической переменной называется переменная, принимающая значения из множества слов или словосочетаний некоторого естественного или искусственного языка.

Терм-множеством называется множество допустимых значений лингвистической переменной.

Задание значения переменной словами, без использования чисел, для человека более естественно. Ежедневно мы принимаем решения на основе лингвистической информации типа: "очень высокая температура"; "длительная поездка"; "быстрый ответ"; "красивый букет"; "гармоничный вкус" и т.п. Психологи установили, что в человеческом мозге почти вся числовая информация вербально перекодируется и хранится в виде лингвистических термов. Понятие лингвистической переменной играет важную роль в нечетком логическом выводе и в принятии решений на основе приближенных рассуждений. Формально, лингвистическая переменная определяется следующим образом.

Лингвистическая переменная задается пятеркой , где - имя логической переменной; - терм-множество, каждый элемент которого (терм) представляется как нечеткое множество на универсальном множестве ; - синтаксические правила, часто в виде грамматики, порождающие название термов; - семантические правила, задающие функции принадлежности нечетких термов, порожденных синтаксическими правилами .

Пример

Рассмотрим лингвистическую переменную с именем - температура в комнате".

Тогда универсальное множество . Терм-множество можно определить как ={"холодно", "комфортно", "жарко"} с следующими функциями принадлежности:

Множество синтаксических правил , порождающее новые термы с использованием квантификаторов {"не", "очень" и "более-менее"};

Семантические правила заданы в виде таблицы расчета функций принадлежности

Квантификатор	Функция принадлежности
не t
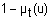
очень t
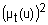
более-менее t

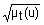
Графики функций принадлежности термов "холодно", "не очень холодно", "комфортно", "более-менее комфортно", "жарко" и "очень жарко" лингвистической переменной "температура в комнате" показаны на рис. 8.1.

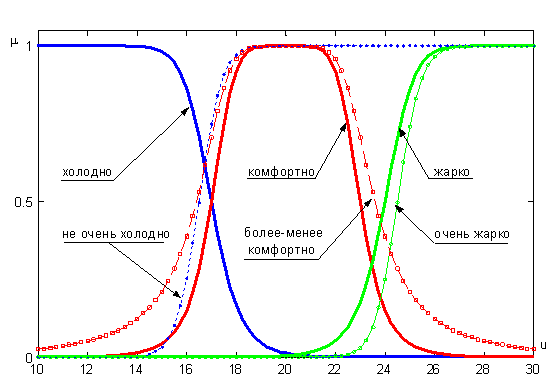
Рис. 8.1- Лингвистическая переменная "температура в комнате"