7.3. Операции над нечеткими множествами.

Над нечеткими множествами можно производить различные операции, при этом необходимо определить их так, чтобы в частном случае, когда множество является четким, операции переходили в обычные операции теории множеств, то есть операции над нечеткими множествами должны обобщать соответствующие операции над обычными множествами. При этом обобщение может быть реализовано различными способами, из-за чего какой-либо операции над обычными множествами может соответствовать несколько операций в теории нечетких множеств.

Пусть и - нечеткие множества.

Множество является подмножеством множества , если:

(7.4)

Пример

Если - множество чисел, очень близких к 10, а - множество чисел, близких к 10, то .

Два нечетких множества и равны тогда и только тогда, когда равны их функции принадлежности.

Объединением нечетких множеств и называется наименьшее нечеткое подмножество, включающее как , так и , с функцией принадлежности

(7.5)

Пересечением нечетких множеств и называется наибольшее нечеткое подмножество, содержащееся одновременно в и , с функцией принадлежности

(7.6)

Разностью нечетких множеств и называется нечеткое множество с функцией принадлежности

(7.7)

Дополнением нечеткого множеств и называется нечеткое множество , функция принадлежности которого определяется следующим образом:

(7.8)

Дизъюнктивной суммой нечетких множеств и называется нечеткое множество с функцией принадлежности

(7.9)

Пример

Пусть заданы множества и :

Очевидно, что .

7.3. Наглядное представление операций над нечеткими множествами.

Наглядное представление основных операций представлено следующим образом.

На рисунке рассматривается прямоугольная система координат, на оси ординат которой откладываются значения , на оси абсцисс в произвольном порядке располагаются элементы . Если по своей природе упорядочено, то этот порядок желательно сохранить в расположении элементов на оси абсцисс.

Рис. 7.3. Нечеткое множество

На рис 7.3 заштрихованная часть соответствует нечеткому множеству .

Рис. 7.4. Нечеткое множество

Рис. 7.5. Нечеткое множество

Рис. 7.6. Нечеткое множество

Пример.

Пусть - нечеткое множество "от 5 до 8") и - нечеткое множество "около 4", заданные своими функциями принадлежности:

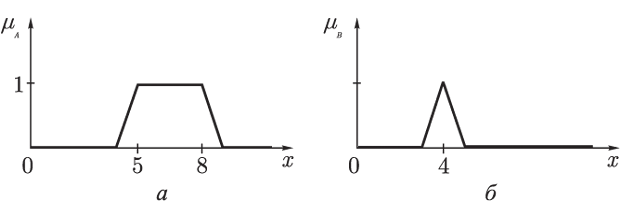
Рис. 7.7.

Тогда, операции пересечения, объединения и дополнения могут быть представлены следующим образом:

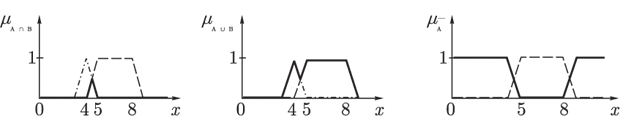
Рис. 7.8.

7.4. Свойства основных операций над нечеткими множествами.

Пусть А, В, С - нечеткие множества, тогда выполняются следующие свойства:

15. Коммутативный закон

(7.8)

16. Ассоциативный закон

(7.9)

17. Дистрибутивный закон

(7.10)

18. Закон де Моргана

(7.11)

19. Закон идемпотентности

(7.12)

20. Операции с пустым множеством:

, (7.13)

где - пустое множество с функцией принадлежности

21. Операции с универсумом:

(7.14)

22. Представление разности через объединение и дополнение

(7.15)

23. Представление дизъюнктивной суммы через объединение и дополнение

(7.16)

В отличие от четких множеств, для нечетких множеств в общем случае:

(7.17)

(7.18)