6.6. Биномиальная формула (бином Ньютона).
Часто при решении комбинаторных задач используется биномиальная теорема (бином Ньютона).
Биномиальная теорема.
(6.14)
Доказательство.
Перемножим
последовательно (a+b)
n раз. Получим
сумму 2n
слагаемых вида d1d2...dn,
где di (i=1,…,n)
равно либо a,
либо b.
Разобьем все слагаемые на n+1
группу B0,B1,…,Bn,
относя к группе Bk
все те произведения, в которых b
встречается множителем k
раз, а a
— n–k
раз. Число элементов в Bk
очевидно равно
(таким числом способов среди n
произведений d1d2...dn
можно выбрать k
сомножителей, равных b),
а каждый элемент в Bk
равен
.
Отсюда и получаем формулу (6.14).
Пример.
Используя
биномиальную теорему, получить формулу
для расчета
и
Решение.
7. Нечеткие множества
7.1. Введение
Пожалуй, наиболее поразительным свойством человеческого интеллекта является способность принимать правильные решения в обстановке неполной и нечеткой информации. Построение моделей приближенных рассуждений человека и использование их в компьютерных системах будущих поколений представляет сегодня одну из важнейших проблем науки.
Значительное продвижение в этом направлении сделано 30 лет тому назад профессором Калифорнийского университета (Беркли) Лотфи А. Заде (Lotfi A. Zadeh). Его работа "Fuzzy Sets", появившаяся в 1965 году в журнале Information and Control, № 8, заложила основы моделирования интеллектуальной деятельности человека и явилась начальным толчком к развитию новой математической теории.
Что же предложил Заде? Во-первых, он расширил классическое канторовское понятие множества, допустив, что характеристическая функция (функция принадлежности элемента множеству) может принимать любые значения в интервале (0;1), а не только значения 0 либо 1. Такие множества были названы им нечеткими (fuzzy). Л.Заде определил также ряд операций над нечеткими множествами и предложил обобщение известных методов логического вывода modus ponens и modus tollens.
Введя затем понятие лингвистической переменной и допустив, что в качестве ее значений (термов) выступают нечеткие множества, Л.Заде создал аппарат для описания процессов интеллектуальной деятельности, включая нечеткость и неопределенность выражений.
Дальнейшие работы профессора Л.Заде и его последователей заложили прочный фундамент новой теории и создали предпосылки для внедрения методов нечеткого управления в инженерную практику.
7.2. Основные определения.
Подход к формализации понятия нечеткого множества состоит в обобщении понятия принадлежности. В обычной теории множеств существует несколько способов задания множества. Одним из них является задание с помощью характеристической функции, определяемой следующим образом.
Пусть
—
так называемое универсальное множество,
из элементов которого образованы все
остальные множества, рассматриваемые
в данном классе задач, например множество
всех целых чисел, множество всех гладких
функций и т.д.
Характеристической
функцией множества
называется
функция, значения которой указывают,
является ли
элементом
множества
:
(7.1)
(7.2)
Особенностью этой функции является бинарный характер ее значений.
С
точки зрения характеристической функции,
нечеткие множества есть естественное
обобщение обычных множеств, когда мы
отказываемся от бинарного характера
этой функции и предполагаем, что она
может принимать любые значения на
отрезке
.
В
теории нечетких множеств характеристическая
функция называется функцией
принадлежности,
а ее значение
—
степенью принадлежности элемента
нечеткому
множеству
.
Нечетким множеством называется совокупность пар
(7.3)
Пример.
Пусть
универсум
,
а множество
задано
Тогда,
очевидно, что элемент
не
принадлежит множеству
,
элемент
принадлежит
ему в малой степени, элемент
более
или менее принадлежит, элемент
принадлежит
в значительной степени,
является
элементом множества
.
Пример.
Пусть универсум есть множество действительных чисел. Нечеткое множество , обозначающее множество чисел, близких к 10, можно задать следующей функцией принадлежности:
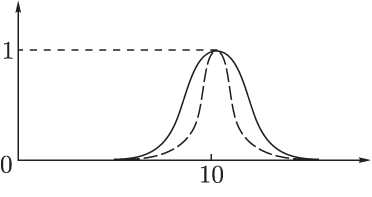
Рис. 7.1.
Показатель
степени
выбирается
в зависимости от степени близости к 10.
Так для описания множества чисел, очень
близких к 10, можно положить
;
для множества чисел, не очень далеких
от 10,
.
Для описания множеств, представляющих собой некоторые понятия или качества, вводится понятие лингвистической переменной. Лингвистическая переменная - это переменная, значениями которой являются не числа, а слова или предложения естественного (или формального) языка.
Пример
Лингвистическая переменная "возраст" может принимать следующие значения: "очень молодой", "молодой", "среднего возраста", "старый", "очень старый" и др. Ясно, что переменная "возраст" будет обычной переменной, если ее значения — точные числа; лингвистической она становится, будучи использованной в нечетких рассуждениях человека.
Каждому значению лингвистической переменной соответствует определенное нечеткое множество со своей функцией принадлежности. Так, лингвистическому значению "молодой" может соответствовать функция принадлежности, изображенная на 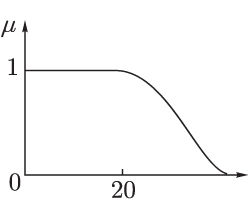рис. 7.2.
Рис.
7.2.