
- •Конспект лекций
- •1. Теория множеств.
- •1.1. Множества
- •1.1.1. Свойства подмножеств.
- •1.1.2 Операции над множествами.
- •1.1.3 Алгебра теории множеств.
- •1.1.4 Решение уравнений алгебры множеств.
- •1.2. Кортеж.
- •1.2.1 Проекция множества.
- •1.2.2 График и свойства графика
- •1 .2.3. Свойства графиков.
- •1.3. Соответствия и отношения
- •1.3.1. Прямое (декартовое) произведение множество.
- •1.3.2. Соответствия.
- •1.3.2.1. Свойства соответствий.
- •1.3.3. Отношения.
- •1 .3.3.1. Операции над отношениями.
- •1.3.3.2 Основные свойства отношений.
- •1.4. Решетки.
- •1.4.1 Диаграммы Хассе.
- •1.4.2 Алгебраическое представление решеток.
- •2. Математическая логика
- •2.1. Высказывания
- •2.1.1. Высказывания и операции над высказываниями.
- •2.1.2. Операции над высказываниями.
- •2.2. Формулы математической логики.
- •2.2.1. Формулы равносильности.
- •2.3. Представление произвольной функции алгебры логики в виде формулы алгебры логики
- •2.4. Различные формы представления высказываний
- •2.5. Выполнимость формулы алгебры логики
- •Выполнимые.
- •2.6. Применение математической логики.
- •2.7. Минимизация сложных высказываний.
- •2.7.1. Метод Квайна.
- •2.7.2. Метод минимизирующих карт.
- •2.7.3. Метод минимизации с помощью карт Вейча.
- •2.8. Булевые функции и их свойства.
- •2.8.1. Функциональная полнота. Теорема Поста.
- •2.9. Логика предикат.
- •2.9.1. Логические операции над предикатами.
- •2.9.2. Квантовые операции.
- •2.9.3. Равносильные формулы логики предикатов.
- •2.9.4. Предваренная нормальная форма предиката
- •3. Теория графов
- •3.1. Основные понятия теории графов.
- •Перечислением:
- •Множеством образов:
- •Матрицей инцидентности
- •Матрицей смежности
- •3.2. Эйлеров граф.
- •3.3. Ядро графа.
- •3.3.1. Множество внутренней устойчивости графа
- •3.3.1.1. Алгоритм Магу для определения множества внутренней устойчивости графа
- •3.3.2. Множество внешней устойчивости графа
- •3.3.2.1. Алгоритм Магу для определения множества внешней устойчивости.
- •3.4. Множество путей в графе
- •3.5. Минимальный путь в графе.
- •3.5.1. Алгоритм фронта волны.
- •3.6. Ярусно-параллельная форма графов
- •3.6.1. Алгоритм приведения графа к ярусно-параллельной форме.
- •3.7. Деревья и леса
- •3.7.1. Алгоритм получения дерева из графа
- •4. Теория алгоритмов
- •4.1. Рекурсивная функция
- •4.2. Машина Тьюринга
- •4.2.1. Работа машины Тьюринга
- •4.3. Нормальные алгоритмы Маркова
- •4.3.1. Работа нормального алгоритма Маркова
- •5. Теория автоматов
- •5.1. Законы функционирования автоматов.
- •5.2. Задание автоматов
- •5.3. Минимизация автоматов
- •5.3.1. Алгоритм минимизации автомата Мили
- •5.3.2. Особенности минимизации автомата Мура.
- •5.3.3. Минимизация частичных автоматов.
- •5.4. Переход от автомата Мили к автомату Мура
- •5.5. Переход от автомата Мура к автомату Мили
- •6. Комбинаторика
- •6.1. Основные понятия.
- •6.2. Перестановки.
- •6.3. Размещения.
- •6.4. Сочетания.
- •6.5. Треугольник Паскаля.
- •6.6. Биномиальная формула (бином Ньютона).
- •7. Нечеткие множества
- •7.1. Введение
- •7.2. Основные определения.
- •7.3. Операции над нечеткими множествами.
- •7.3. Наглядное представление операций над нечеткими множествами.
- •7.4. Свойства основных операций над нечеткими множествами.
- •7.5. Алгебраические операции над нечеткими множествами.
- •8. Нечеткая логика.
- •8.1. Лингвистические переменные
- •8.2. Нечеткая истинность
- •8.3. Нечеткие логические операции
- •9. Литература
3.4. Множество путей в графе
По
матрице смежности можно определить,
сколько различных путей существует
между i-той
и j-
той вершинами длиной в к
единиц. Для этого необходимо определить
матрицу
![]() ,
где
- матрица смежности.
,
где
- матрица смежности.
Если
элемент
![]() матрицы
:
матрицы
:
![]() -
между i-той
и j-
той вершины не существует пути длиной
в к
единиц;
-
между i-той
и j-
той вершины не существует пути длиной
в к
единиц;
![]() -
между i-той
и j-
той вершины существуют
различных
путей длиной в к
единиц;
-
между i-той
и j-
той вершины существуют
различных
путей длиной в к
единиц;
Если - нулевая матрица, это означает, что графе нет путей в к единиц, а максимальный путь – это путь длиной в (к -1) единиц.
3.5. Минимальный путь в графе.
Одной из самых распространенных задач в теории графов является задача поиска минимального пути в графе.
Рассмотрим некоторые свойства минимальных путей
Любой минимальный путь является простым путем.
Если путь
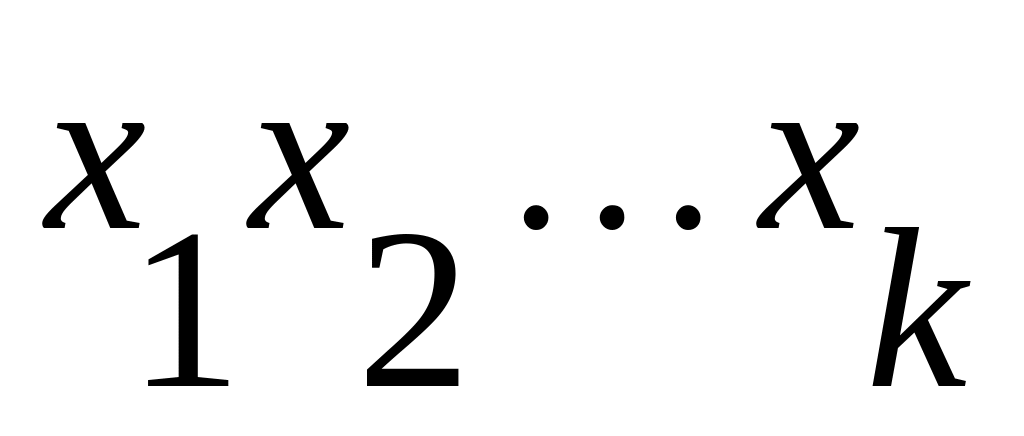 - минимальный,
то любые пути
- минимальный,
то любые пути
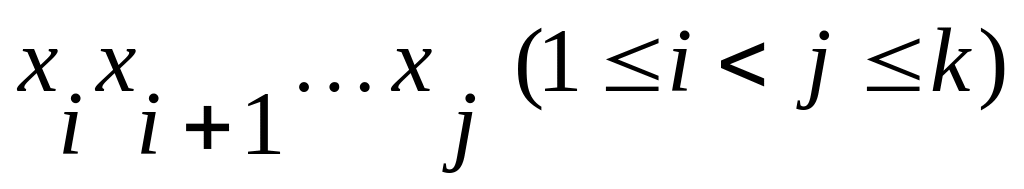 внутри
минимального пути также будут минимальны.
внутри
минимального пути также будут минимальны.
Пусть Г-1х – прообраз вершины xi – это множество вершин, из которых исходят дуги в вершину xi.
Одним из алгоритмов поиска минимального пути в графе является алгоритм фронта волны (FW –Front Wave)
3.5.1. Алгоритм фронта волны.
Пусть
необходимо найти минимальный путь из
вершины
в вершину
![]() .
.
Выписываются все вершины с 1 по n. Вершина помечается индексом 0.
Находится первый фронт волны
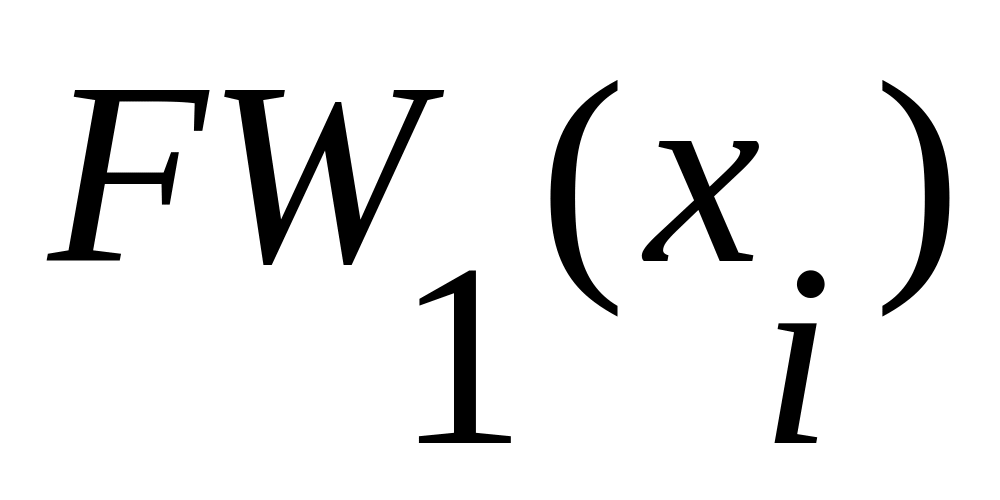 как множество вершин образа вершины
.
как множество вершин образа вершины
.
![]() (3.17)
(3.17)
Все вершины, принадлежащие первому фронту волны, помечаются индексом 1.
Вводится счетчик шагов (фронтов волны)
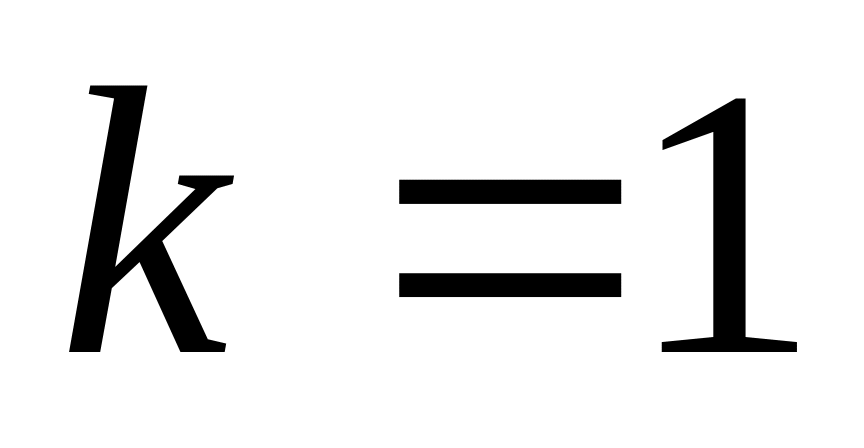 .
.Если
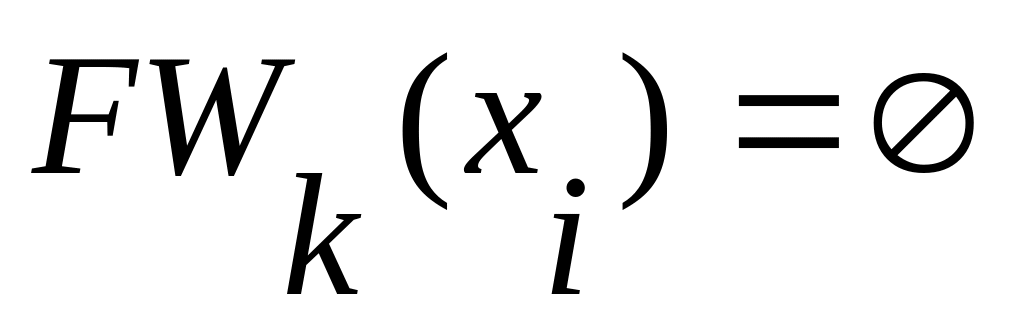 или
или
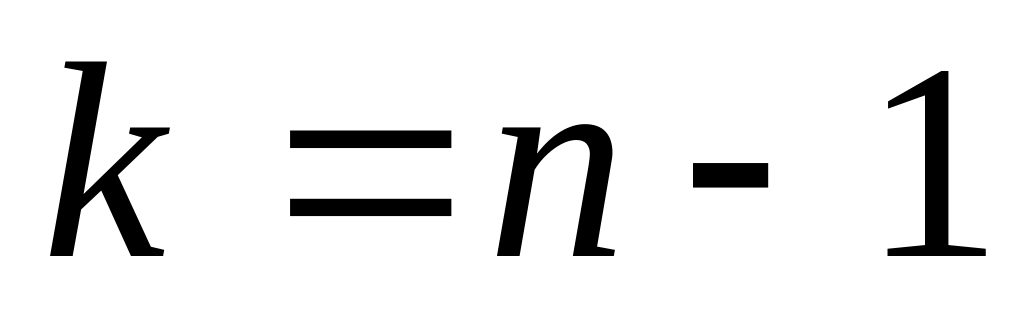 ,
то вершина
недостижима из вершины, и работа
алгоритма на этом заканчивается. В
противном смысле переходим к пункту
6.
,
то вершина
недостижима из вершины, и работа
алгоритма на этом заканчивается. В
противном смысле переходим к пункту
6.Если
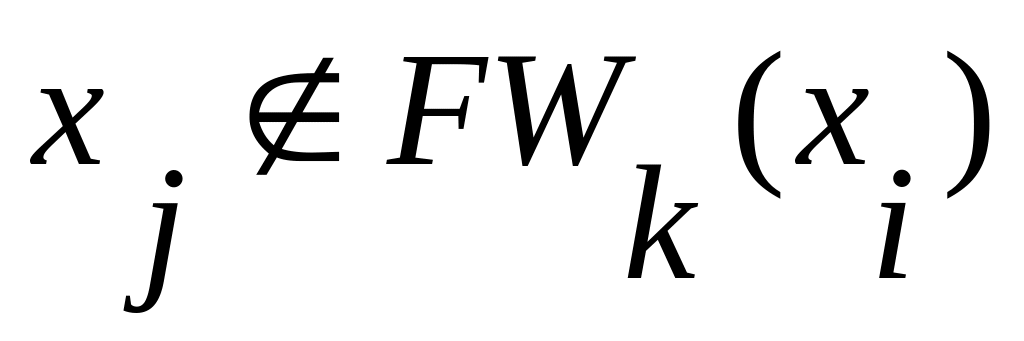 ,
то переходим к пункту 8. В противном
случае существует путь из вершины
в вершину
длиной в
,
то переходим к пункту 8. В противном
случае существует путь из вершины
в вершину
длиной в
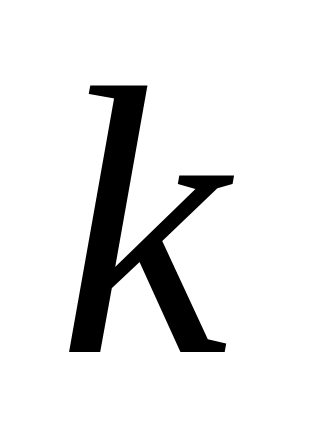 единиц, и этот путь минимальный:
единиц, и этот путь минимальный:
![]()
Находятся промежуточные вершины
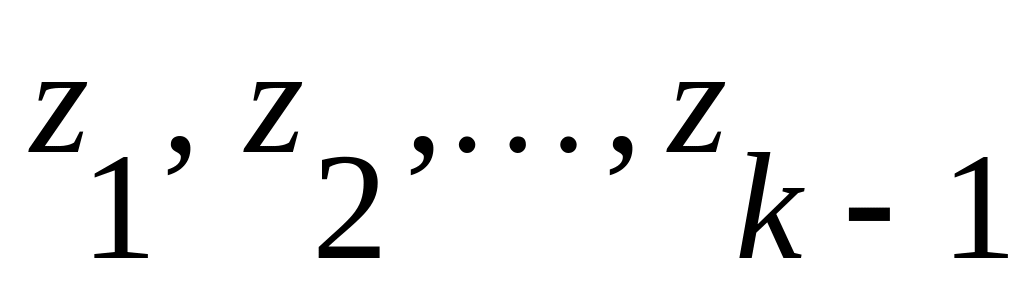 z
по правилу:
z
по правилу:
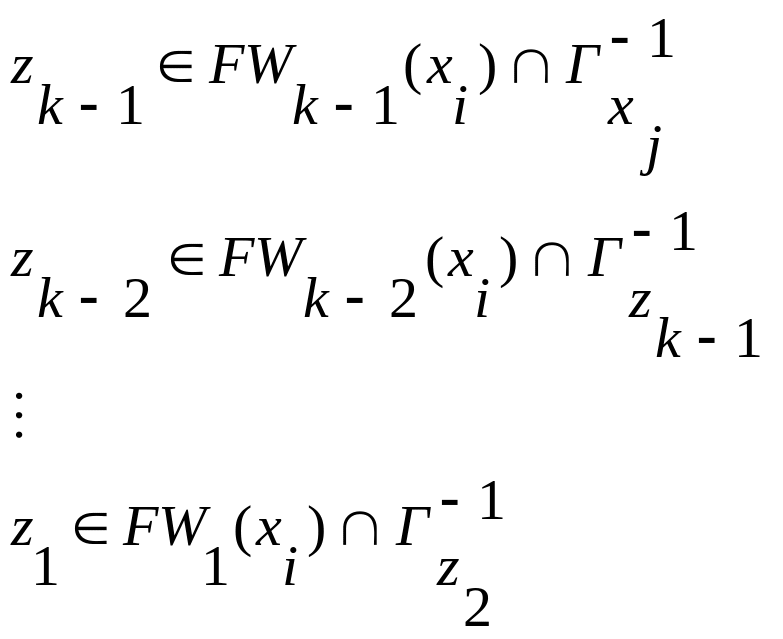 , (3.18)
, (3.18)
где
![]() -
прообраз
вершины
- множество
вершин, из которых заходят дуги в вершину
-
прообраз
вершины
- множество
вершин, из которых заходят дуги в вершину
Определяется
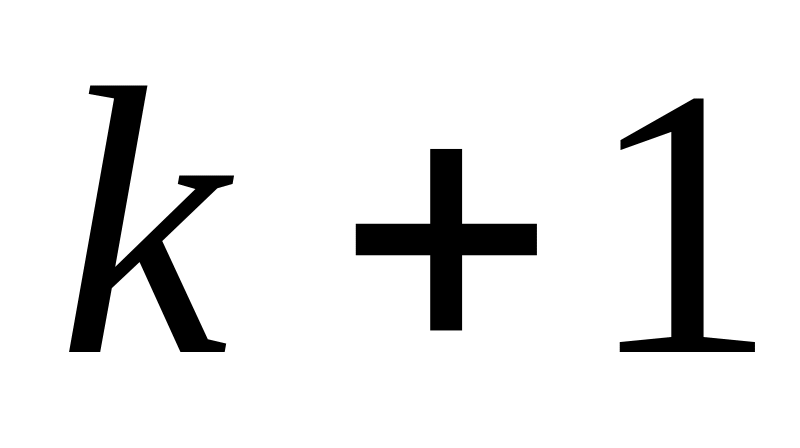 фронт волны как все непомеченные
вершины, принадлежащие образу вершин
- го фронта волны. Помечаются индексом
вершины
фронта волны. Далее осуществляется
переход к пункту 5.
фронт волны как все непомеченные
вершины, принадлежащие образу вершин
- го фронта волны. Помечаются индексом
вершины
фронта волны. Далее осуществляется
переход к пункту 5.
ПРИМЕР
Пусть задан граф матрицей смежности:
-
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
Необходимо найти минимальный путь из вершины в вершину (по алгоритму «фронта волны»).
Выпишем все вершины. Вершина помечается индексом «0»
0
![]()
Находится первый фронт волны:
![]()
Все вершины, принадлежащие первому фронту волны, помечаются индексом «1».
0 1 1
Так как
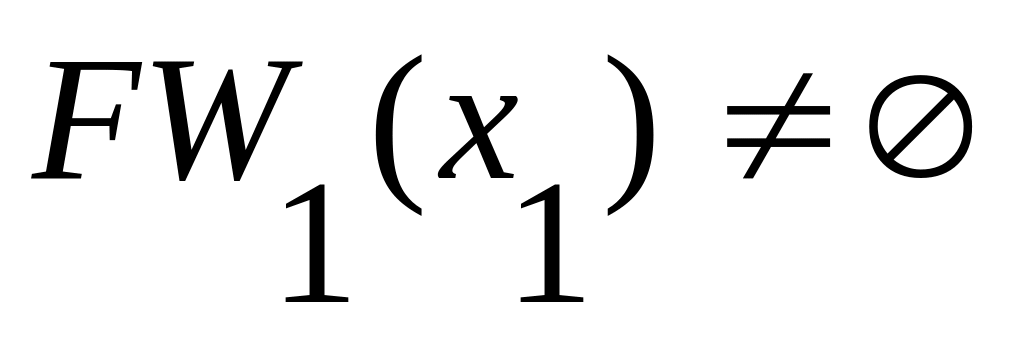 ,
,
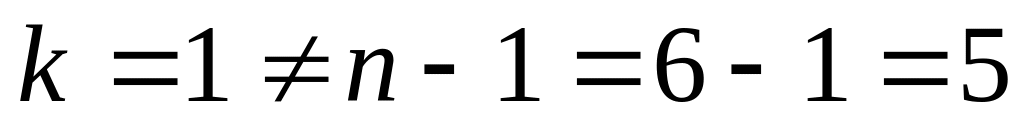 и
и
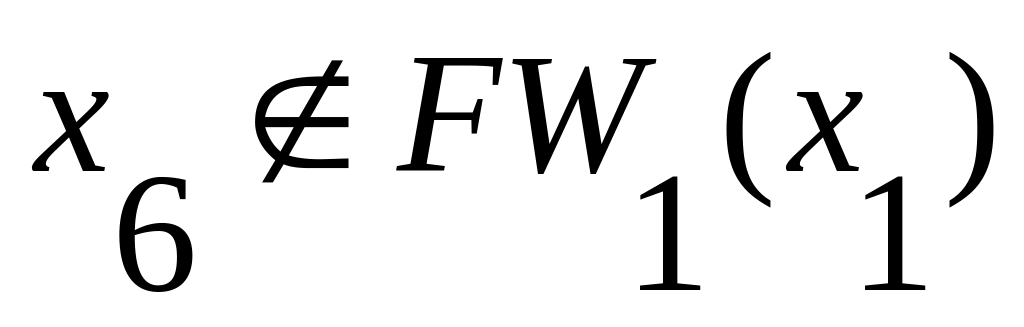 ,
то определяем второй фронт волны:
,
то определяем второй фронт волны:
![]()
Все вершины, принадлежащие второму фронту волны, помечаются индексом «2».
0 2 2 1 1
Так как
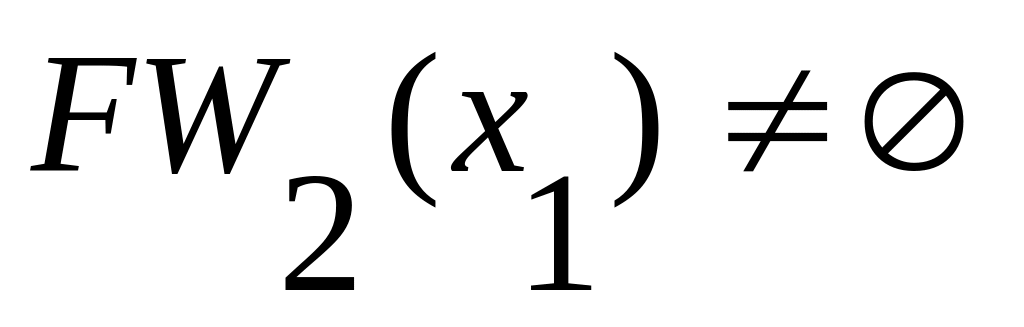 ,
,
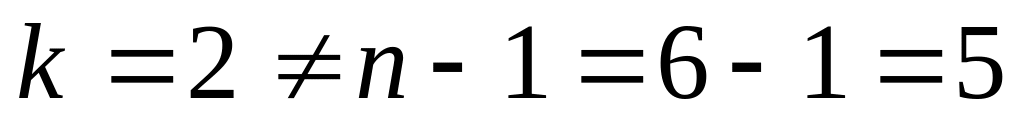 и
и
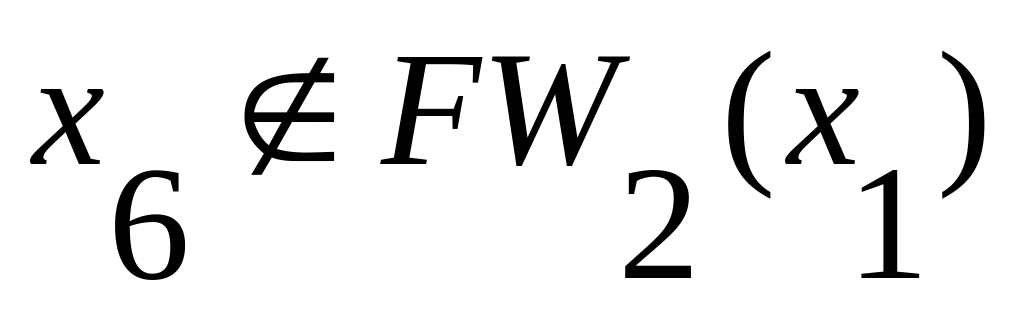 ,
то определяем третий фронт волны:
,
то определяем третий фронт волны:
![]()
Так как
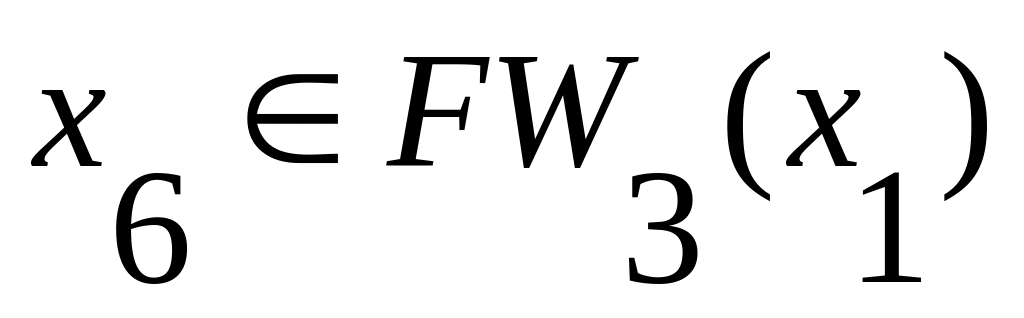 ,
то существует путь из вершины
в вершину
длиной 3 единицы:
,
то существует путь из вершины
в вершину
длиной 3 единицы:
![]()
Находятся промежуточные вершины
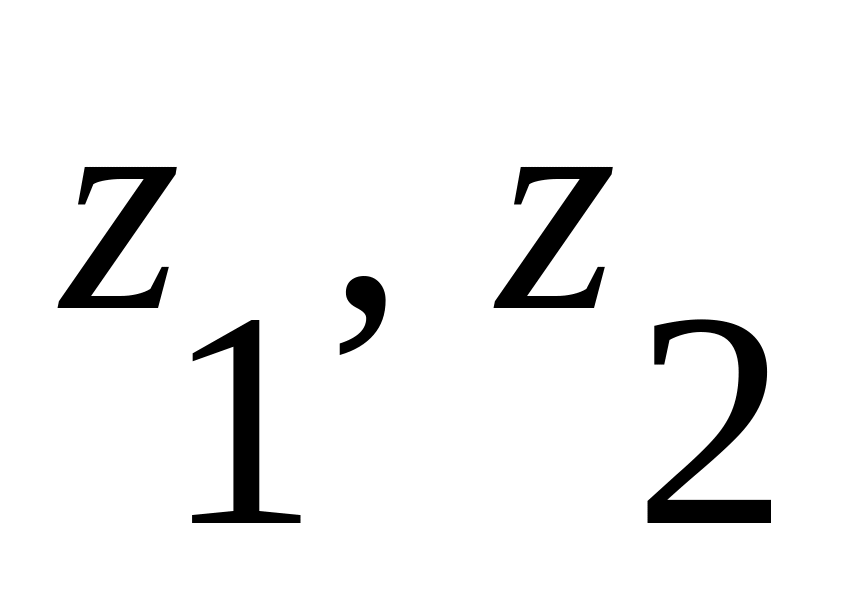 :
:
![]()
Выберем
![]()
![]()
Выберем
![]()
Таким образом, минимальный путь из вершины в вершину имеет вид:
![]()
