3.3.2. Множество внешней устойчивости графа

Множество внешней устойчивости – множество вершин, для которых выполняется одно из следующих правил:

1). Любая вершина входит в это множество

2) Либо вершина не входит в это множество, но из этой вершины есть дуга в данное множество.

Пусть дан граф . Тогда для множества внешней устойчивости справедливо следующее:

(3.12)

Число внешней устойчивости (β) – это наименьшая мощность из всех множеств внешней устойчивости.

3.3.2.1. Алгоритм Магу для определения множества внешней устойчивости.

Пусть дан граф . Для данного графа существует множество внешней устойчивости .

Вводятся булевые переменные и по тому же правилу, что и для алгоритма Магу для определения множества внутренней устойчивости.

Тогда определение множества внешней устойчивости (3.12) запишется следующим образом:

(3.13)

Для справедливо следующее

(3.14)

Данное уравнение лежит в основе алгоритма Магу

Алгоритм Магу состоит из следующих этапов:

1. Для графа составляется матрица смежности

2. Матрица смежности дополняется единицами (1) по главной диагонали.

3. Для каждой строки выписываются дизъюнкции.

4. Выражение приводится к ДНФ.

5. Все вершины, входящие в элементарную конъюнкцию, образуют множество внешней устойчивости

ПРИМЕР

Определить множество внешней устойчивости для графа, представленного на рис. 3.7.

Матрица смежности имеет вид:

		1	1	1
	1
	1
			1

Дополним матрицу смежности единицами по главной диагонали

	1	1	1	1
	1	1
	1		1
			1	1

Для каждой строки выписываются дизъюнкции:

(3.15)

Приведем выражение к ДНФ:

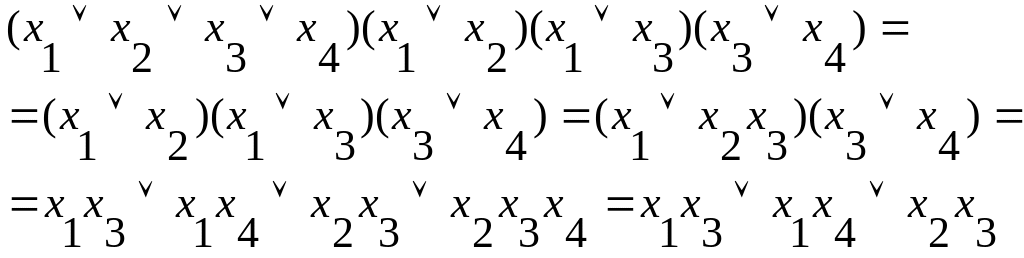(3.16)

Множества внутренней устойчивости:

Числом внешней устойчивости = 2.

Ядром графа называется подмножество вершин, являющихся одновременно внутренней и внешней устойчивостью.

Граф, представленный на рис. 3.7. имеет ядро