2.7. Минимизация сложных высказываний.

Существует несколько способов минимизации сложных высказываний. Рассмотрим самые распространенные:

• метод Квайна;

• карты Вейча;

• минимизирующие карты.

2.7.1. Метод Квайна.

Алгоритм метода Квайна включает в себя следующие этапы:

1. Любая формула приводится к СДНФ.

2. СДНФ приводится к сокращенной ДНФ (СкДНФ). При получении СкДНФ используются следующие формулы равносильности:

а) Формула склеивания

б) Формула неполного склеивания

в) Формула поглощения

Применяя все возможные процедуры склеивания, СДНФ приводится к СкДНФ.

3. Минимальная форма формулы (МДНФ ) получается на основе импликантной матрицы путем нахождения минимального покрытия этой матрицы. Импликанта – это элементарная конъюнкция СкДНФ. Конституента единицы – это элементарная конъюнкция СДНФ. Импликантная матрица – это матрица импликант и констиуент единиц. (столбцы - конституенты единицы, строки – импликанты). МДНФ может быть несколько.

ПРИМЕР.

Необходимо найти МДНФ формулы:

1 2 3 4 5 6

Осуществляем всевозможные склеивания

1-2

1-4

2-3

3-6

4-5

5-6

СкДНФ имеет вид:

Составляем импликантную матрицу

	+	+
	+			+
		+	+
			+			+
				+	+
					+	+

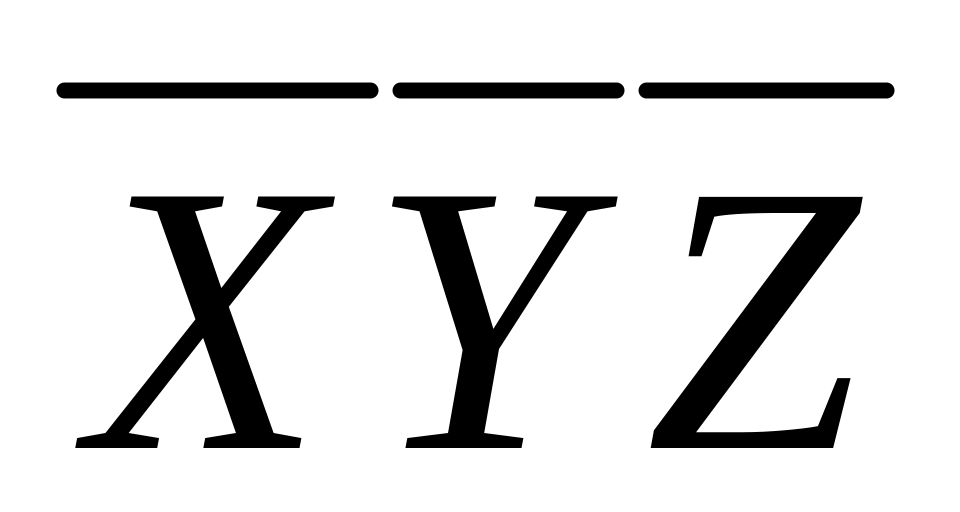
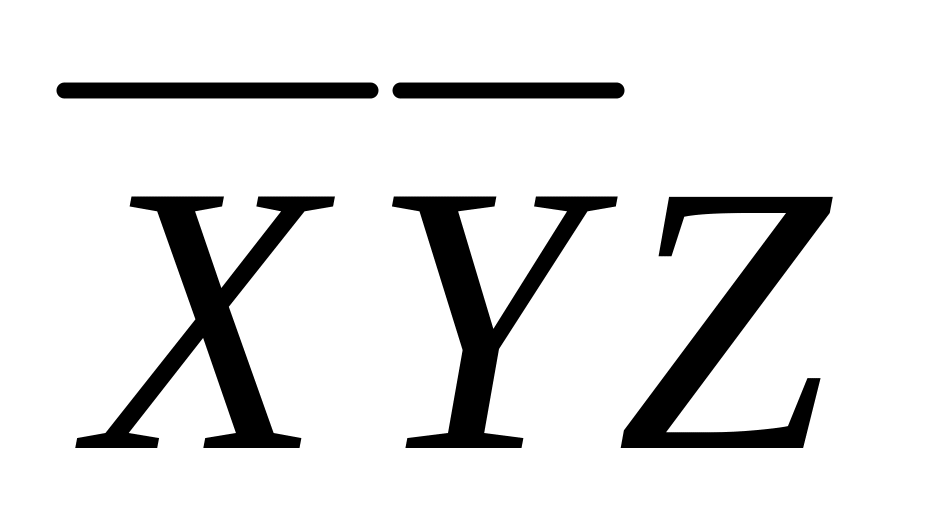
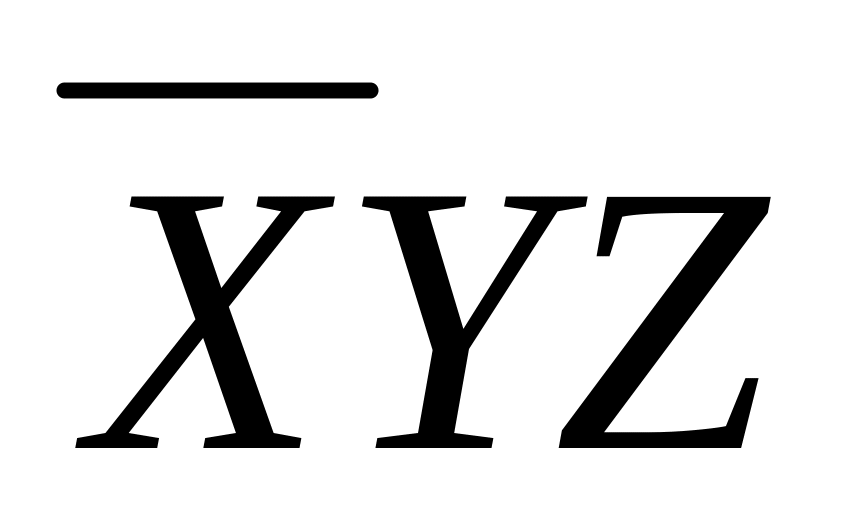
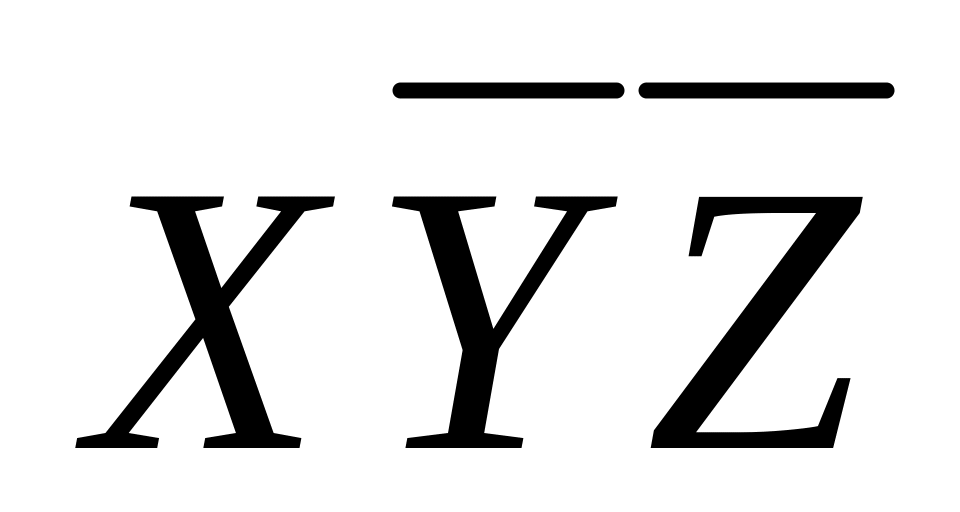
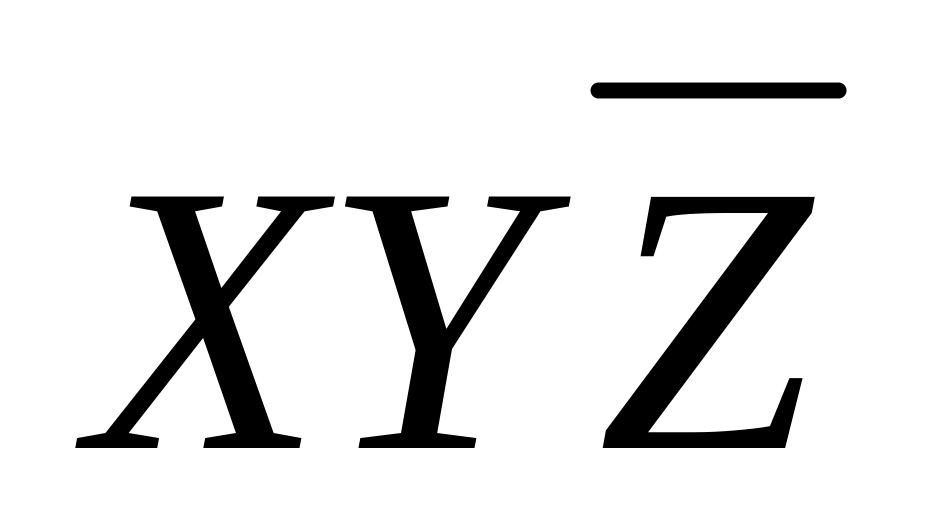
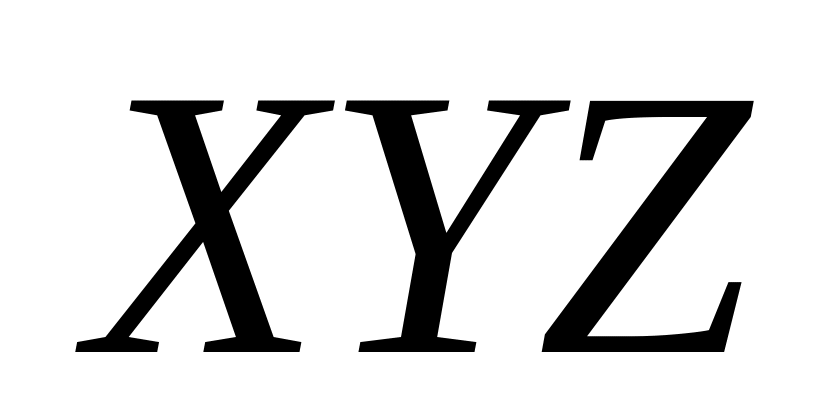
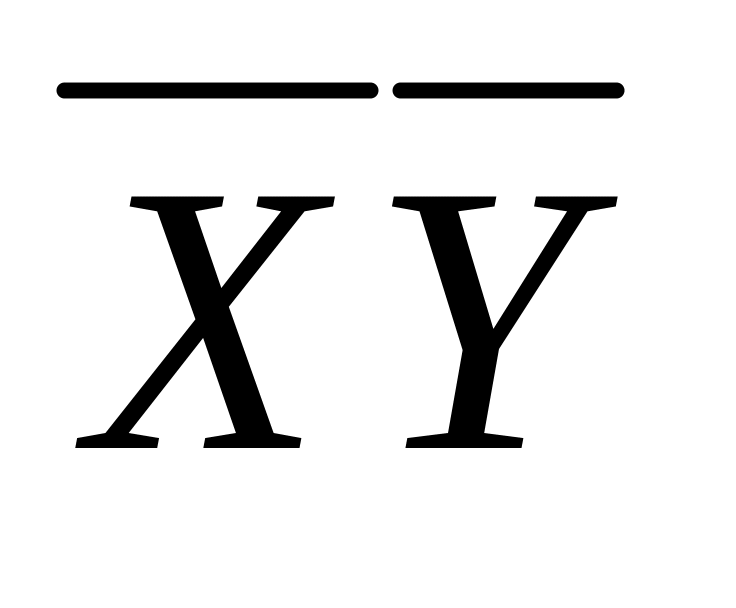
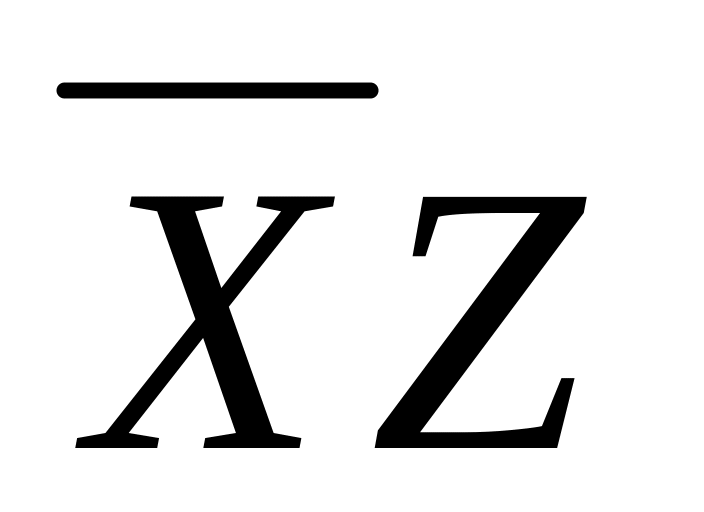
По данной импликантной матрице можно выбрать следующие МДНФ

2.7.2. Метод минимизирующих карт.

Алгоритм метода минимизирующих карт включает в себя следующие этапы:

1. Любая формула приводится к СДНФ.

2. Составляется таблица всевозможных сочетаний переменных.

3. Из таблицы вычеркиваются те строки, которые не содержат конституенты СДНФ. Конъюнкции этих строк вычеркиваются в других строках.

4. В каждой строке оставляются конъюнкции с минимальным количеством переменных.

5. Из каждой строки выбирается олна конъюнкция и составляется ДНФ.

6. Из построенных ДНФ выбирается минимальная.

ПРИМЕР

Дана СДНФ

							*
							*

* - помечены строки, не содержащие конституенты СДНФ.

После соответствующих преобразований получаем следующую таблицу

							*
							*

После всевозможного перебора остаются следующие МДНФ: