Лабораторная работа 4 исследование переходного сопротивления контакта

Цель работы: произвести экспериментальные исследования зависимости переходного сопротивления контакта от сипы нажатия, от состояния контактной поверхности, от материала контакта; аналитический расчет переходных сопротивлений по эмпирическим формулам; сопоставление экспериментальных данных с расчетными.

1. Общие положения

Электрическим контактом называется место соприкосновения двух проводников, позволяющее проводить электрический ток. Сами проводники называются контактными элементами или просто контактами.

Контактные поверхности, как бы тщательно они не были обработаны, представляют собой неровную поверхность с выступами и впадинами. По этой причине соприкосновение контактных поверхностей происходит не по всей поверхности, а лишь в отдельных точках [1-3].

Вследствие этого происходит стягивание линий тока к точкам соприкосновения и повышение вблизи них плотности тока. Примерная картина этого явления представлена на рис. 4.1.

Благодаря нажатию одного контакта на другой вершины выступов сминаются и образуются площадки действительного касания контактов.

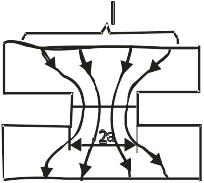
Рис. 4.1. Примерная картина прохождения тока в электрическом контакте

Рассмотрим процесс перехода тока из одного контакта в другой при касании двух цилиндрических контактов по торцам.

Положим, что контакты имеют только одну площадку касания и что эта площадка имеет форму круга с радиусом (рис.4.2.)

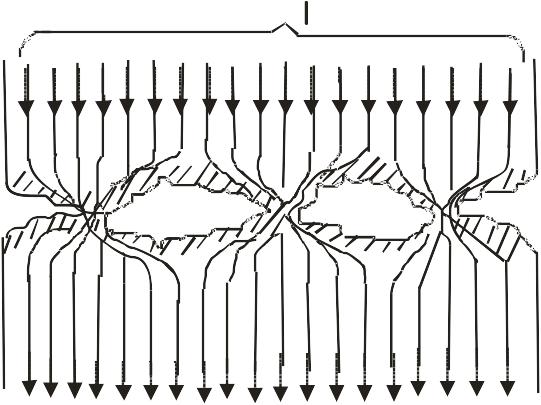
Рис. 4.2.Картина прохождения тока в идеализированном контакте

Величину радиуса при пластической деформации можно найти с по мощью формулы

, (4.1)

где - сила начатия контактов; - временное сопротивление материала контактов смятию.

В результате стягивания линий тока к площадке касания с радиусом путь тока меняется. Сечение проводника, через которое фактически проходит ток, становится меньше, что вызывает увеличение сопротивления. Сопротивление в области точки касания, обусловленное явлениями стягивания тока, называется переходным сопротивлением контакта.

Картина растекания тока в области стягивания рис. 4.2 аналогична картине растекания тока из плоского диска радиусом в полубесконечную среду. Учитывая, что размеры области стягивания малы по сравнению с размерами тела контакта, реальные контакты можно заменить полу бесконечными телами. Для двух полубесконечных тел, контактирующих по одной круглой площадке касания, картина поля тока и электрических потенциалов представлена на рис.4.3.

Эквипотенциальные поверхности являются полуэллипсоидами вращения, линии тока - гиперболами с общим фокусом. Для такой идеализирован ной картины растекания тока переходное сопротивление контактов определяется по формуле [3,4]

, (4.2)

где - удельное электрическое сопротивление материала контактов, Ом·см;

- радиус площадки соприкосновения, см.

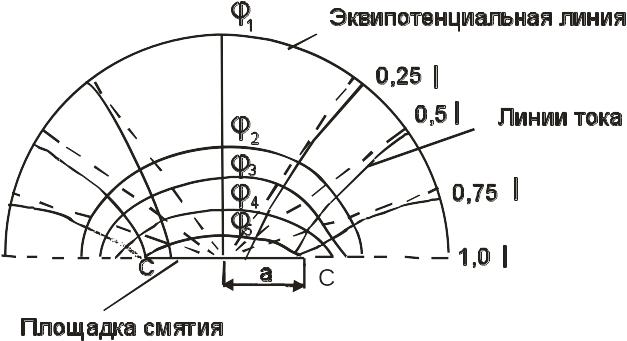
Рис.4.3.Идеализированная картина растекания тока в точечном контакте

С точностью до 5% эта формула справедлива, если поперечные размеры контакта превосходят в 13 раз диаметр площадки касания.

В большинстве практических случаев это условие соблюдается, так как размеры площадки касания обычно не превосходят долей миллиметра.

Находя из (4.1) радиус площадки и подставляя его значение в (4.2), получаем:

. (4.3)

Таким образом, переходное сопротивление контактов пропорционально удельному электрическому сопротивлению материала контактов, корню квадратному из временного сопротивления на смятие материала и обратно пропорционально корню квадратному из силы нажатия на контакты.

В табл.4.1 приводятся экспериментальные значения коэффициента для одноточечных свежезачищенных контактов.

Одноточечный контакт применяется только при малых токах. При больших токах применяется многоточечный контакт. Поскольку ток проходит через несколько контактных переходов, включенных параллельно, переходное сопротивление уменьшается по сравнению с одноточечным контактом. Количество контактирующих точек увеличивается с ростом силы нажатия по весьма сложному закону. Для такого контакта переходное сопротивление выражается уравнением. [1]

.

Показатель изменяется от 0,5 до 1,0 и учитывает число контактных площадок, характеризующих форму контактных поверхностей. При точечном контакте контактирующая точка одна, ; при линейном контакте контактирующих точек не менее двух ; при плоскостном контакте контактирующих точек не менее трех .

Сопротивление зависит и от обработки поверхности. Шлифовка ведет к тому, что на поверхности остаются более пологие выступы с большим сечением. Смятие таких выступов возможно только при больших силах нажатия. Поэтому сопротивление шлифованных контактов выше, чем контактов с более грубой обработкой.

Таблица 4.1

Материал контактов	Коэффициент k для сильноточных контактов,	Коэффициент k для слаботочных контактов (реле),
Медь	1,0	0,14 - 0,175
Серебро	0,5	0,06
Олово	5,0	-
Латунь	6,7	-
Сталь	7,6	-
Алюминий	1,6	-