Лабораторная работа 1 исследование электродинамических усилий между двумя параллельными шинами конечной длины прямоугольного сечения

Цель работы: определить экспериментальным и аналитическим методами значения усилий (ЭДУ) между двумя параллельными шинами конечной длины прямоугольного сечения.

1. Общие положения

Во время аварийных режимов в сети некоторые типы электрических аппаратов подвергаются действию токов короткого замыкания, величина которых может в десятки и даже сотни раз превышать номинальные токи. Протекающие токи вызывают в аппаратуре электродинамические усилия. Конструкция электрических аппаратов должна рассчитываться с учетом действия этих усилий. В связи с этим, расчет электродинамических усилий, действующих между элементами токоведущих цепей аппарата или между аппаратами, представляет большой интерес.

1.1. Методы расчета электродинамических усилий

Существует несколько методов расчета электродинамических усилий в аппаратах. Наибольшее распространение получили два метода:

1) метод, основанный на использовании закона Био-Саварра-Лапласа;

2) по изменению запаса магнитной энергии системы.

Первый метод применяется тогда, когда можно аналитически найти индукцию в той точке проводника, для которого определяют силу. Так, например, если по проводнику длиной l , расположенному в магнитном поле с индукцией В, протекает ток і, то сила действующая на проводник, равна

(1.1)

где - угол между направлением вектора магнитной индукции и направлением тока.

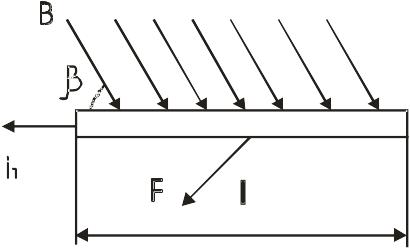
Рис.1.1. Проводник с током в магнитном поле

Направление действия силы может быть определено по правилу левой.

Второй метод определения электродинамических усилий основан на использовании энергетического баланса системы проводников с током. Если пренебречь электростатической энергией системы и принять, что при деформации токоведущих контуров или их перемещении под действием электродинамических усилий величина тока во всех контурах остается неизменной, то силу можно найти по уравнению:

(1.2)

где - электромагнитная энергия; - возможное перемещение в направлении действия силы . Таким образом, сила равна частной производной от электромагнитной энергии данной системы по координате, в направлении которой действует сила. Силы, действующие в контуре с током, стремятся изменить конфигурацию контура так, чтобы охватываемый контуром магнитный поток увеличился.

1.2. Расчет сил между параллельными проводниками

Рассмотрим вначале задачу для бесконечно тонких проводников, расположенных в одной плоскости на расстоянии и обтекаемых токами , (рис. 1.2.) Расчет будем производить на основании закона Био-Савара-Лапласа, согласно которому элементарная индукция от элемента тока в месте расположения элемента проводника равна:

(1.3)

где - магнитная проницаемость воздуха, равная Гн/м;

- угол между током , и лучом от к рассматриваемому элементу .

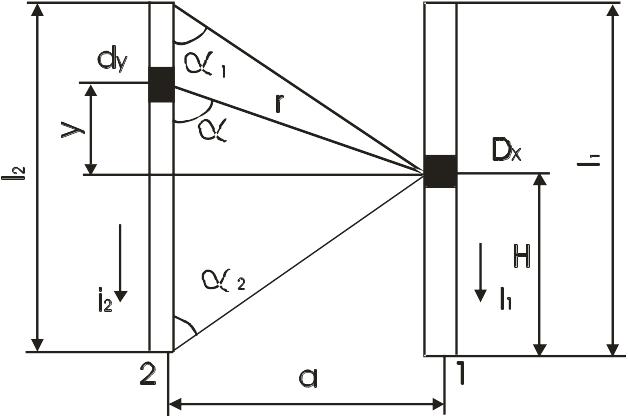
Рис. 1.2. К расчету ЭДУ между параллельными проводниками

Полная индукция от проводника . в элементе

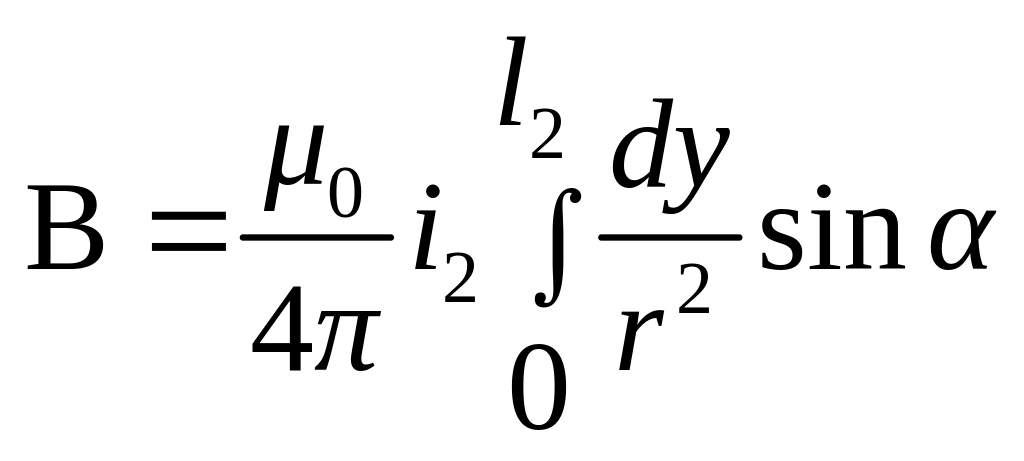(1.4)

Элементарная сила, действующая на , обтекаемый током , может быть определена на основании (1.1):

(1.5)

Так как по условию задачи проводники расположены в одной плоскости, а вектор индукции перпендикулярен плоскости, то

.

Учитывая это к (1.4), выражение (1,5) можно переписать

. (1.6)

Если проинтегрировать по всей длине проводника , то получим полную силу, действующую между проводниками:

. (1.7)

Так как токи неизменны по длине проводника, то выражение (1.7) можно переписать в виде произведения

. (1.8)

В этом выражении первый множитель зависит только от токов. Второй - от взаимного геометрического расположения проводников и представляет безмерную величину, ее называют геометрическим коэффициентом контура .

Тогда

, (1.9)

т.е. сила взаимодействия между двумя проводниками с токами и пропорциональна произведению этих токов и зависит от геометрии проводников.

Подставив в (1.9) Гн/м, получим

(1.10)

Выразим подынтегральные переменные второго интеграла через угол :

Считая, что проводник 2 распространяется от до , чему соответствует изменение угла от до , запишем

. (1.11)

Если проводник имеет конечную длину, то согласно (1.10):

(1.12)

Знак минус указывает, что при одинаковых направлениях токов проводники будут притягиваться.

В случае, если оба проводника будут иметь конечную длину , пределы интегрирования для (1.11) будут от до и

(1.13)

В том случае, когда расстояние между проводниками значительно меньше их длины , то K_г и сила определяется выражением (1.12). При , расчет по формуле (1.12) дает погрешность не более 5% (в сторону увеличения).

Для двух параллельных проводников разной длины, расположенных с любым сдвигом, можно воспользоваться формулой:

,

где - сумма диагоналей трапеции, построенной на взаимодействующих проводниках;

- сумма боковых сторон этой трапеции;

- расстояние между проводниками.

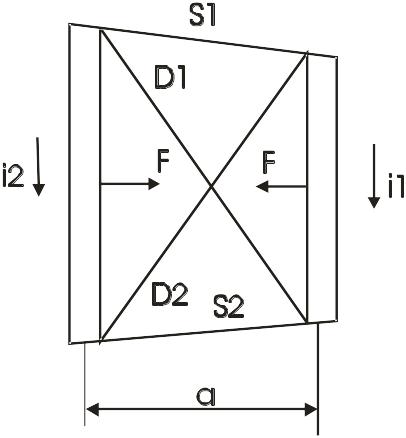
Рис.1.3. К расчету ЭДУ между параллельными проводниками разной длины

Установлено, что для проводников круглого и трубчатого сечения, форма сечения не оказывает влияния на величину электродинамических усилий. В этом случае принимают, что ток идет по геометрической оси.

Для шин прямоугольного сечения форма сечения влияет на величину электродинамических усилий и ее можно учесть коэффициентом формы (определить по рис. 1.4). С учетом формы сечения проводника

. (1.14)

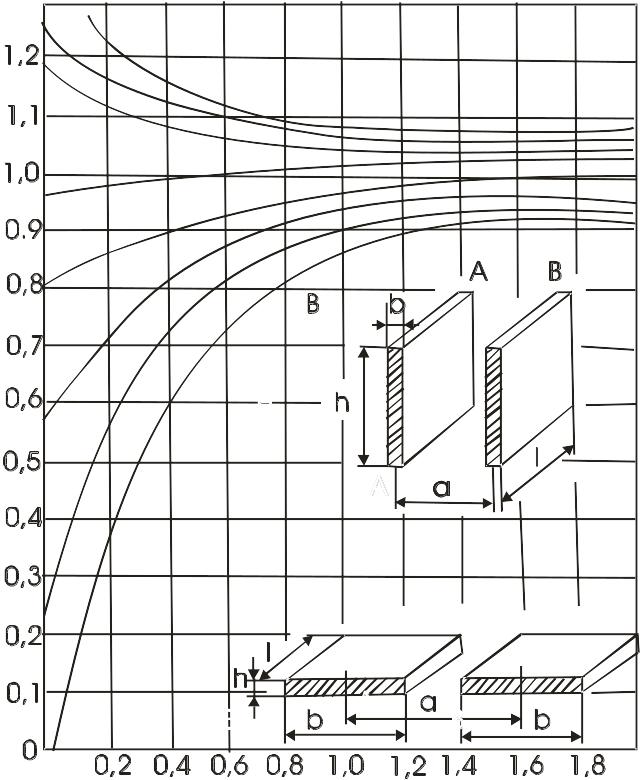
Рис. 1.4. Графики для определения коэффициента формы сечения проводника