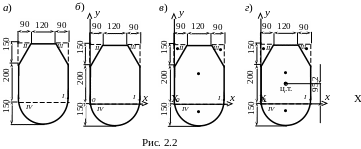
В рассматриваемом примере представлено поэтапное построение чертежа. Каждому этапу соответствует свой сектор рисунка (см. весь рисунок 2.2). Иными словами, сколько этапов, столько чертежей. Такой приём использован для наглядности объяснения. В процессе решения соответствующей задачи студенту не стоит повторять данные действия. Достаточно все построения выполнить на одном чертеже.

2. Выбираем и показываем на чертеже вспомогательную систему координат. После выполнения второго пункта чертёж принимает вид, показанный на рис. 2.2, б, где представлена вспомогательная система координат x0y.

3. П оказываем центры тяжести простых составляющих (фигур) сечения. После выполнения третьего пункта чертёж принимает вид, показанный на рис. 2.2, в. Точками отмечены центры тяжести простых составляющих. На рис. 2.3 указано положение центров тяжести геометрических фигур, форму которых имеют простые составляющие рассматриваемого сечения.

4. Зная положение центров тяжести простых составляющих, определяем их координаты относительно вспомогательной системы координат. Здесь и далее b – ширина фигуры (горизонтальный размер), h – высота фигуры (вертикальный размер).

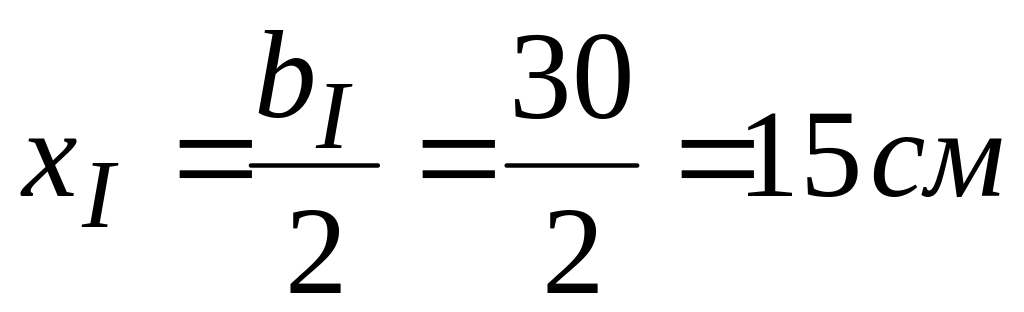
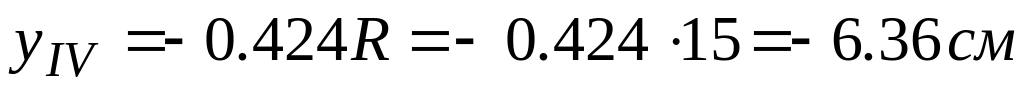
5. Вычисляем площади простых фигур (составляющих).

, ,

, .

2. Вычисляем координаты центра тяжести всего сечения относительно вспомогательной системы координат.

Так как сечение симметричное, то одну координату центра тяжести сечения можно определить без вычислений (центр тяжести находится на оси симметрии). В данном случае известна координата x_с: .

Для того, чтобы вычислить координату y_с, следует воспользоваться формулой (7), приведённой в § 1.2, преобразовав её для рассматриваемого случая следующим образом:

2. Показываем на чертеже центр тяжести сечения. После выполнения данного пункта чертёж примет вид, представленный на рис. 2.2, г.

Первая часть задачи выполнена.

Часть II: вычисляем главные центральные моменты инерции сечения.

1. Строим главные центральные оси сечения , .

Чтобы оси были центральными, их необходимо провести через центр тяжести сечения. Чтобы они при этом стали главными, хотя бы одна из них должна совпадать с осью симметрии сечения. В данном случае ось совпадает с осью симметрии сечения. После построения чертёж принимает вид, показанный на рис. 2.4, а.

2. Проводим параллельно главным центральным осям сечения центральные оси простых составляющих, после чего чертёж принимает вид, показанный на рис. 2.4, б.

3. Вычисляем момент инерции сечения относительно главной центральной оси

Поскольку сечение сложное для выполнения пункта 3 следует воспользоваться первой формулой (13) § 1.5. Применительно к данному случаю, она запишется следующим образом:

,

, , , - моменты инерции прямоугольника (фигура I), прямоугольных треугольников (фигуры II, III), полукруга (фигура IV) относительно

главной центральной оси всего сечения, которая не совпадает с собственными центральными осями x_I, x_II, x_III, x_IV прямоугольника, треугольников, полукруга (см. рис.2.4, б), соответственно.

Рассмотрим первое слагаемое. Формулы моментов инерции прямоугольника относительно его собственных центральных осей известны (§ 1.4). Применительно к рассматриваемому случаю соответствующая формула примет вид:

,

г де - момент инерции прямоугольника относительно его центральной оси .

Для перехода от собственной центральной оси простой составляющей к главной центральной оси всего сечения следует воспользоваться формулой перехода между параллельными осями (18). Применительно к рассматриваемой ситуации роль компоненты формулы (18) играет момент инерции прямоугольника относительно главной центральной оси всего сечения , а компоненты - момент инерции прямоугольника относительно его собственной центральной оси . Теперь, чтобы определить момент инерции , формула (18) должна быть представлена в следующем виде:

,

где – расстояние между осями и .

Рассуждая аналогичным образом, вычислим остальные слагаемые исходной формулы.

,

где , , – расстояния между осями и , , (см. рис. 2.4, б).

Подставляем полученные значения в общую формулу:

.

4. Вычисляем момент инерции сечения относительно главной центральной оси y_с.

Рассмотрим вторую формулу (13). Для данной задачи она запишется следующим образом

.

Вычислим все слагаемые записанного выражения по аналогии с предыдущим пунктом.

,

,

где - расстояние между собственной центральной осью треугольника и главной центральной осью всего сечения.

,

.

Подставляем полученные значения в общую формулу:

Вторая часть задачи выполнена.

Задача 2.2

Требуется: 1) определить положение центра тяжести составного сечения, показанного на рис. 2.5; 2) вычислить главные центральные моменты инерции сечения; 3) определить моменты сопротивления составного сечения относительно главных центральных осей.

Решение.