1.4 Моменты инерции сечений в форме простых геометрических фигур

Д ля простых геометрических фигур (прямоугольник, треугольник, круг и т.д.) с помощью соотношений (9), (10), (12) не представляет труда получить формулы моментов инерции относительно двух произвольных взаимно перпендикулярных осей, компонентами которых являются основные габаритные размеры этих фигур. В основе данных манипуляций лежит процедура непосредственного интегрирования.

Прямоугольник.

Определим осевые моменты инерции прямоугольника высотой h и шириной b относительно осей , , , (рис. 1.5).

Двумя прямыми линиями, параллельными осям x и , обозначим на прямоугольнике элементарную площадку шириной b, высотой dy, площадь которой .

Расстояние этой площадки до оси x равно y. Воспользуемся выражением (9). Пределы интегрирования в рассматриваемом случае h и 0:

.

Аналогичные умозаключения позволяют получить выражение для момента инерции прямоугольника относительно оси y: .

Пределы интегрирования становятся равными и , когда момент инерции определяется относительно оси . Расстояние от данной оси до элементарной площадки становится равным (см. рис .1.5). С помощью выражения (9) получаем:

.

Аналогично получается момент инерции прямоугольника относительно оси : .

• Иными словами, для приведённого на рис. 1.5 расположения осей формулы осевых моментов инерции прямоугольника имеют вид:

, , , .

В случае необходимости таким же образом можно получить формулы для моментов инерции прямоугольника относительно других осей, параллельных его сторонам.

Треугольник.

Используя выше приведённую методику, получим моменты инерции треугольника относительно осей , , , (рис. 1.6).

Д вумя прямыми линиями, параллельными осям x и , обозначим на треугольнике элементарную площадку, расположенную на расстоянии y от оси x и на расстоянии от оси , шириной и высотой dy. Ширина полоски величина переменная и зависит от координат y или (в зависимости от того, какая ось рассматривается - или ). Площадь данного элемента .

Так как ширина полоски является функцией от координат, для дальнейшей работы следует получить выражение, описывающее зависимость между этими параметрами. Рассматривая два подобных треугольника с основаниями b и или b и , высотами h и или h и (см. рис. 1.6), можно составить пропорции:

и ,

из которых следует:

и .

На основании данных пропорций и выражений (9), получим:

.

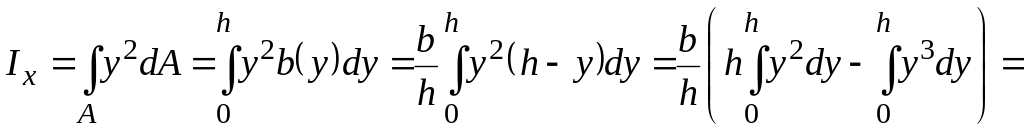
Рассуждая аналогично, можно получить формулу для момента инерции прямоугольного треугольника относительно оси y:

.

Таким же образом получим формулу для момента инерции прямоугольного треугольника относительно оси : .

• То есть для приведённого на рис. 1.5 расположения осей формулы осевых моментов инерции треугольника имеют вид:

, , , .

Круг.

Определим момент инерции круга диаметром D относительно его центральных осей. Выделим элементарное кольцо радиусом ρ и толщиной dρ, площадь которого, соответственно, .

Поскольку все элементарные площадки , образующие кольцо, расположены на равном расстоянии ρ от центра, выражение (10) можно интерпретировать следующим образом:

.

Так как для круга , то согласно соотношению (11):

,

из чего следует, что

.

• Следовательно, для круга, координатные оси которого расположены, как показано на рис. 1.7, моменты инерции определяются формулами:

, , .