Предисловие

О дной из составляющих расчётов на прочность, жёсткость и устойчивость конструктивных элементов является анализ геометрических характеристик поперечных сечений.

Например, надёжность подвеса, на котором крепится груз (рис.1), зависит от величины площади поперечного сечения подвеса. Естественно, чем больше площадь, тем выше способность данного конструктивного элемента сопротивляться силе, передаваемой на него от груза. Площадь является простейшей геометрической характеристикой поперечного сечения.

При других видах нагружения площади поперечного сечения не достаточно для оценки надёжности элемента.

Например, величина прогиба двух одинаковых консолей с прямоугольным поперечным при равной нагрузке будет различной, если по-разному ориентировать поперечные сечения консолей. При вертикальном расположении большего размера (рис.2, а) прогиб меньше, чем при горизонтальном (рис.2, б).

Е сли рассмотреть две колонны с круглым и прямоугольным поперечными сечениями одинаковой площади, одинаковой длины и из одного материала, сжимающая нагрузка к которым прикладывается в торцовых сечениях, на пересечениях их осей симметрии (рис.3), то выясниться, что колонна с прямоугольным сечением потеряет устойчивость (искривиться) при нагрузке, меньшей, чем колонна с круглым сечением. Причём искривление произойдёт в плоскости, параллельной наименьшему размеру прямоугольного сечения, то есть в плоскости наименьшего сопротивления данной колонны сжимающей нагрузке. У колонны с круглым сечением, теоретически, все плоскости в этом плане равноценны. Поэтому трудно заранее предугадать в какой плоскости произойдёт искривление такой колонны. Требуется знание дополнительных факторов, обусловленных не только геометрией.

Из всего выше сказанного следует, что при анализе конструктивных элементов в ряде случаев необходимо учитывать наряду с размерами поперечных сечений их форму и расположение по отношению к действующей нагрузке. А значит должны существовать геометрические характеристики поперечных сечений, отражающие эти факторы.

1. Теоретические сведения

1.1 Площадь и статические моменты сечения Площадь представляет собой простейшую геометрическую характеристику сечения.

Если сечение представить в виде совокупности элементарных площадок площадью (рис. 1.1), то площадь всего сечения A будет определяться соотношением вида:

,

(1)

где имеет место интегрирование по всей площади сечения.

Совместив координатную плоскость x0y и плоскость поперечного сечения бруса, например, как это показано на рис.1.1, можно по аналогии с моментом силы относительно оси получить моменты элемента площади относительно координатных осей

; ,

именуемые статическими моментами элемента площади относительно осей x и y, соответственно. В представленных соотношениях x и y – координаты элемента площади сечения.

Тогда совокупность произведений элементарных площадей на алгебраические значения их расстояний до соответствующей оси по всей площади сечения является статическим моментом всего сечения относительно данной оси:

, , (2)

где , - статические моменты поперечного сечения относительно оси x и оси y, соответственно.

Если установить аналогию между системой параллельных сил и совокупностью элементарных площадок, то аналогично центру системы параллельных сил [7, стр. 123-124], должен существовать некий центр всего сечения. Его называют центром тяжести сечения. Тогда на основании теоремы Вариньона о моменте равнодействующей силы относительно произвольной оси и соотношения (2) можно утверждать, что статические моменты сечения относительно координатных осей x и y могут быть определены как:

; ,

(3)

где и - координаты центра тяжести сечения.

Статический момент сечения измеряется в единицах длины в третьей степени: мм³, см³ и т. д.

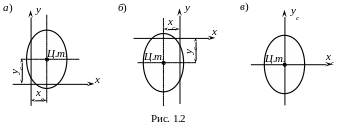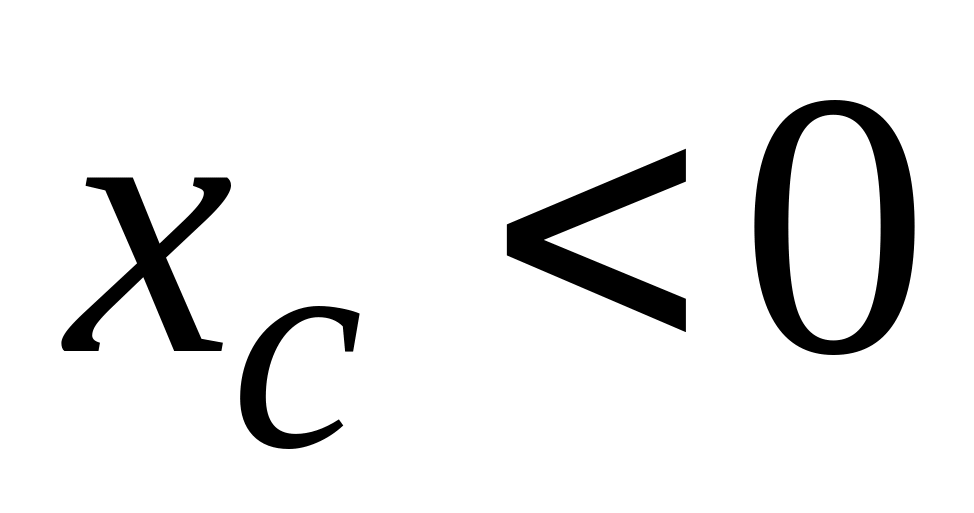• В зависимости от расположения координатных осей относительно центра тяжести сечения, статические моменты сечения могут быть больше нуля (рис. 1.2, а) - , ; меньше нуля (рис. 1.2, б) - , и равны нулю (рис. 1.2, в) - .

Координатные оси, проходящие через центр тяжести сечения, называют центральными осями (см. рис. 1.2, в).

Если известны статические моменты сечения относительно некоторых координатных осей, то согласно соотношениям (3), координаты центра тяжести сечения можно определить с помощью формул:

; .

(4)