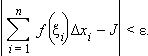- •Дайте определение понятий «объединение множеств», «пересечение множеств». Изобразите объединение, пересечение множеств а и в с помощью кругов Эйлера
- •Дайте определение понятий «разность множеств», «дополнение множества». Изобразите разность и дополнение множеств а и в с помощью кругов Эйлера
- •Дайте определение понятий «матрица», «размерность матрицы», «элемент матрицы», «индексы элемента матрицы». Опишите операцию умножения матриц, транспонирование матриц
- •Дайте определение понятий «матрица», «размерность матрицы», «элемент матрицы», «индексы элемента матрицы». Опишите свойства, используемые для преобразования строк матрицы
- •Дайте определение понятия «определитель второго порядка». Запишите и объясните формулу его вычисления. Продемонстрируйте на примерах вычисление определителей
- •Дайте определение понятия «определитель третьего порядка». Запишите и объясните формулу его вычисления. Продемонстрируйте на примерах вычисление определителей
- •Дайте определение понятия «система линейных уравнений». Сформулируйте теорему Крамера. Охарактеризуйте метод решения слау по формулам Крaмера
- •Дайте определение понятия «система линейных уравнений». Сформулируйте условия применения метода Гаусса. Охарактеризуйте метод решения слау методом Гаусса
- •Дайте определение понятия «матричная модель». Изложите и охарактеризуйте основные этапы матричного моделирования
- •Дайте определение понятий «предел числовой последовательности». Сформулируйте основные теоремы о пределах. Опишите правила вычисления пределов
- •Дайте определение понятий «предел функции в точке». Сформулируйте основные теоремы о пределах. Опишите правила вычисления пределов
- •Дайте определение понятий «предел функции на бесконечности». Сформулируйте основные теоремы о пределах. Опишите правила вычисления пределов
- •Дайте определение понятий «функция непрерывная в точке», «точка разрыва функции». Изложите классификацию точек разрыва. Продемонстрируйте на рисунках поведение графика функции в точках разрыва
- •Дайте определение понятия «производная функции в точке». Сформулируйте правила дифференцирования алгебраических функций. Продемонстрируйте их применение
- •Дайте определение понятия «производная функции в точке». Сформулируйте правила дифференцирования сложной функции. Продемонстрируйте их применение
- •Назовите и объясните виды монотонностей функции. Сформулируйте условия возрастания и убывания функции на промежутке и продемонстрируйте их на примере функции
- •Дайте определение понятия «определенный интеграл», объясните свойства определенного интеграла. Охарактеризуйте способ непосредственного интегрирования (формула Ньютона-Лейбница)
- •Дайте определение понятия «определенный интеграл», объясните свойства определенного интеграла. Охарактеризуйте метод интегрирования по частям
- •Дайте определение понятия «определенный интеграл», объясните свойства определенного интеграла. Охарактеризуйте способ интегрирования заменой переменной
- •Дайте определение понятия «криволинейная трaпеция». Изложите виды расположения плоских фигур в системе координат и проанализируйте формулы для вычисления их площадей
- •Назовите виды приложений определенного интеграла. Изложите и проанализируйте способы нахождения объема тела вращения вокруг осей координат
- •Дайте определение понятий «ду 1-го порядка», «решение ду 1-го порядка (общего и частного решений)», «задачи Коши». Опишите решение ду 1-го порядка с разделяющимися переменными
- •Дайте определение понятий «ду 1-го порядка», «решение ду 1-го порядка (общего и частного решений)», «задачи Коши». Опишите решение однородных ду 1-го порядка
- •Дайте определение понятий «ду 1-го порядка», «решение ду 1-го порядка (общего и частного решений)», «задачи Коши». Опишите решение простейших линейных ду 1-го порядка
- •Выскажите общее суждение об упорядоченном множестве. Сформулируйте понятие перестановки из n элементов. Запишите формулу для нахождения числа перестановок. Прокомментируйте правила комбинаторики
- •Дайте определение понятия «граф», опишите его простейшие свойства. Приведите примеры решения задач с использованием графов
- •Дайте определение понятия «вероятность события» (классическое определение вероятности). Сформулируйте теорему сложения и продемонстрируйте примеры ее использования для решения задач
- •Дайте определение понятия «условная вероятность». Сформулируйте теорему умножения и продемонстрируйте примеры ее использования для решения задач
Дайте определение понятия «определенный интеграл», объясните свойства определенного интеграла. Охарактеризуйте способ непосредственного интегрирования (формула Ньютона-Лейбница)
ОТВЕТ:
Число
J
называется определенным
интегралом
от функции f(x) на отрезке [a; b], если
для любого ε > 0 существует
такое n
Є N,
что для разбиения отрезка [a; b] на
равные части n
точками и для любого выбора точек: |
Свойства определенного интеграла:
1.
![]() =b
–
a;
2.
Если f
интегрируема на [a,b],
то она интегрируема на любом [a*,b*],
содержащемся в [a,b].
3.
Пусть a<c<b
и функция интегрируема на [a,c]
и [c,b],
то
=b
–
a;
2.
Если f
интегрируема на [a,b],
то она интегрируема на любом [a*,b*],
содержащемся в [a,b].
3.
Пусть a<c<b
и функция интегрируема на [a,c]
и [c,b],
то![]() .
4.
Если f
и g
интегрируемы на [a,b],
то f+g
также интегрируема на нем и
.
4.
Если f
и g
интегрируемы на [a,b],
то f+g
также интегрируема на нем и
![]() .
5.
Пусть функция f
интегрируема на [a,b],
c=const,
тогда cf
также
интегрируема на [a,b]
и
.
5.
Пусть функция f
интегрируема на [a,b],
c=const,
тогда cf
также
интегрируема на [a,b]
и
![]() .
6.
Если f
и g
интегрируемы на [a,b],
то fg
также интегрируема на [a,b].
7.
Если f(x)
интегрируема на [a,b]
и нижняя грань функции ∣f(x)∣
на [a,b]
положительна, то и функция 1/f(x)
интегрируема на [a,b].
8.
Если f(x)
неотрицательна и интегрируема на [a,b],
то
.
6.
Если f
и g
интегрируемы на [a,b],
то fg
также интегрируема на [a,b].
7.
Если f(x)
интегрируема на [a,b]
и нижняя грань функции ∣f(x)∣
на [a,b]
положительна, то и функция 1/f(x)
интегрируема на [a,b].
8.
Если f(x)
неотрицательна и интегрируема на [a,b],
то
![]() .
Следствие.
Если f
и g
интегрируемы на [a,b]
и для всех x∈[a,b] :
f(x)≥g(x) ,
то
.
Следствие.
Если f
и g
интегрируемы на [a,b]
и для всех x∈[a,b] :
f(x)≥g(x) ,
то![]() .
9.
Пусть функция f
интегрируема на [a,b],
тогда:
.
9.
Пусть функция f
интегрируема на [a,b],
тогда:
![]() ,
,
![]() ,a<b.
10.
Пусть функция f
интегрируема на [a,b],
тогда ∣f(x)∣
также интегрируема на нем и:
,a<b.
10.
Пусть функция f
интегрируема на [a,b],
тогда ∣f(x)∣
также интегрируема на нем и:
![]() ,a<b.
Замечание. Если отказаться от условия
a<b,
то
,a<b.
Замечание. Если отказаться от условия
a<b,
то![]() .
.
Формула
Ньютона-Лейбница.
Если f(x) непрерывна на отрезке [a, b], и
F(x) - некоторая первообразная функции
f(x),
то
![]() .
.
Д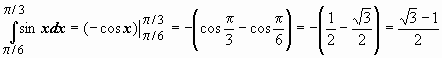 ок-во:
Мы установили, что функция
ок-во:
Мы установили, что функция
![]() -
первообразная непрерывной f(x). Так как
F(x) – тоже первообразная, то Ф(x) = F(x) + C.
Положим в этом равенстве x = a. Так как
-
первообразная непрерывной f(x). Так как
F(x) – тоже первообразная, то Ф(x) = F(x) + C.
Положим в этом равенстве x = a. Так как
![]() ,
то в равенстве
,
то в равенстве![]() переобозначим переменные: для переменной
интегрирования t вернёмся к обозначению
x, верхний предел x обозначим b. Окончательно,
.
переобозначим переменные: для переменной
интегрирования t вернёмся к обозначению
x, верхний предел x обозначим b. Окончательно,
.
![]() Разность
в правой части формулы Ньютона-Лейбница
обозначается специальным символом:
Разность
в правой части формулы Ньютона-Лейбница
обозначается специальным символом:
![]() (здесь
(здесь![]() читается как "подстановка от a до b"),
поэтому формулу Ньютона -Лейбница обычно
записывают так:
читается как "подстановка от a до b"),
поэтому формулу Ньютона -Лейбница обычно
записывают так:![]() .
.
Пример:
Дайте определение понятия «определенный интеграл», объясните свойства определенного интеграла. Охарактеризуйте метод интегрирования по частям
ОТВЕТ:
Число J называется определенным интегралом от функции f(x) на отрезке [a; b], если для любого ε > 0 существует такое n Є N, что для разбиения отрезка [a; b] на равные части n точками и для любого выбора точек: выполняется неравенство:
Свойства определенного интеграла:
1. =b – a; 2. Если f интегрируема на [a,b], то она интегрируема на любом [a*,b*], содержащемся в [a,b]. 3. Пусть a<c<b и функция интегрируема на [a,c] и [c,b], то . 4. Если f и g интегрируемы на [a,b], то f+g также интегрируема на нем и . 5. Пусть функция f интегрируема на [a,b], c=const, тогда cf также интегрируема на [a,b] и . 6. Если f и g интегрируемы на [a,b], то fg также интегрируема на [a,b]. 7. Если f(x) интегрируема на [a,b] и нижняя грань функции ∣f(x)∣ на [a,b] положительна, то и функция 1/f(x) интегрируема на [a,b]. 8. Если f(x) неотрицательна и интегрируема на [a,b], то . Следствие. Если f и g интегрируемы на [a,b] и для всех x∈[a,b] : f(x)≥g(x) , то . 9. Пусть функция f интегрируема на [a,b], тогда: , ,a<b. 10. Пусть функция f интегрируема на [a,b], тогда ∣f(x)∣ также интегрируема на нем и: ,a<b. Замечание. Если отказаться от условияa<b, то .
Метод интегрирования по частям:
Если
u(x), v(x) - непрерывно дифференцируемые
функции, то
![]() .
.
Док-во.
Интегрируем равенство (uv)’=u’v+uv’
в пределах от a до b:
![]() .
.
Ф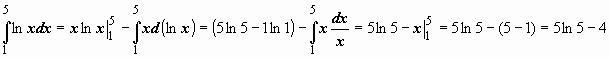 ункция
в левом интеграле имеет первообразную
uv, по формуле Ньютона-Лейбница
ункция
в левом интеграле имеет первообразную
uv, по формуле Ньютона-Лейбница
![]() ,
следовательно,
,
следовательно,
![]() ,
откуда и следует доказываемое равенство.
,
откуда и следует доказываемое равенство.
Пример: