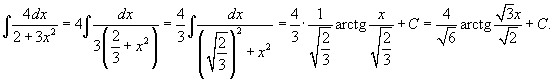- •Дайте определение понятий «объединение множеств», «пересечение множеств». Изобразите объединение, пересечение множеств а и в с помощью кругов Эйлера
- •Дайте определение понятий «разность множеств», «дополнение множества». Изобразите разность и дополнение множеств а и в с помощью кругов Эйлера
- •Дайте определение понятий «матрица», «размерность матрицы», «элемент матрицы», «индексы элемента матрицы». Опишите операцию умножения матриц, транспонирование матриц
- •Дайте определение понятий «матрица», «размерность матрицы», «элемент матрицы», «индексы элемента матрицы». Опишите свойства, используемые для преобразования строк матрицы
- •Дайте определение понятия «определитель второго порядка». Запишите и объясните формулу его вычисления. Продемонстрируйте на примерах вычисление определителей
- •Дайте определение понятия «определитель третьего порядка». Запишите и объясните формулу его вычисления. Продемонстрируйте на примерах вычисление определителей
- •Дайте определение понятия «система линейных уравнений». Сформулируйте теорему Крамера. Охарактеризуйте метод решения слау по формулам Крaмера
- •Дайте определение понятия «система линейных уравнений». Сформулируйте условия применения метода Гаусса. Охарактеризуйте метод решения слау методом Гаусса
- •Дайте определение понятия «матричная модель». Изложите и охарактеризуйте основные этапы матричного моделирования
- •Дайте определение понятий «предел числовой последовательности». Сформулируйте основные теоремы о пределах. Опишите правила вычисления пределов
- •Дайте определение понятий «предел функции в точке». Сформулируйте основные теоремы о пределах. Опишите правила вычисления пределов
- •Дайте определение понятий «предел функции на бесконечности». Сформулируйте основные теоремы о пределах. Опишите правила вычисления пределов
- •Дайте определение понятий «функция непрерывная в точке», «точка разрыва функции». Изложите классификацию точек разрыва. Продемонстрируйте на рисунках поведение графика функции в точках разрыва
- •Дайте определение понятия «производная функции в точке». Сформулируйте правила дифференцирования алгебраических функций. Продемонстрируйте их применение
- •Дайте определение понятия «производная функции в точке». Сформулируйте правила дифференцирования сложной функции. Продемонстрируйте их применение
- •Назовите и объясните виды монотонностей функции. Сформулируйте условия возрастания и убывания функции на промежутке и продемонстрируйте их на примере функции
- •Дайте определение понятия «определенный интеграл», объясните свойства определенного интеграла. Охарактеризуйте способ непосредственного интегрирования (формула Ньютона-Лейбница)
- •Дайте определение понятия «определенный интеграл», объясните свойства определенного интеграла. Охарактеризуйте метод интегрирования по частям
- •Дайте определение понятия «определенный интеграл», объясните свойства определенного интеграла. Охарактеризуйте способ интегрирования заменой переменной
- •Дайте определение понятия «криволинейная трaпеция». Изложите виды расположения плоских фигур в системе координат и проанализируйте формулы для вычисления их площадей
- •Назовите виды приложений определенного интеграла. Изложите и проанализируйте способы нахождения объема тела вращения вокруг осей координат
- •Дайте определение понятий «ду 1-го порядка», «решение ду 1-го порядка (общего и частного решений)», «задачи Коши». Опишите решение ду 1-го порядка с разделяющимися переменными
- •Дайте определение понятий «ду 1-го порядка», «решение ду 1-го порядка (общего и частного решений)», «задачи Коши». Опишите решение однородных ду 1-го порядка
- •Дайте определение понятий «ду 1-го порядка», «решение ду 1-го порядка (общего и частного решений)», «задачи Коши». Опишите решение простейших линейных ду 1-го порядка
- •Выскажите общее суждение об упорядоченном множестве. Сформулируйте понятие перестановки из n элементов. Запишите формулу для нахождения числа перестановок. Прокомментируйте правила комбинаторики
- •Дайте определение понятия «граф», опишите его простейшие свойства. Приведите примеры решения задач с использованием графов
- •Дайте определение понятия «вероятность события» (классическое определение вероятности). Сформулируйте теорему сложения и продемонстрируйте примеры ее использования для решения задач
- •Дайте определение понятия «условная вероятность». Сформулируйте теорему умножения и продемонстрируйте примеры ее использования для решения задач
Дайте определение понятий «функция непрерывная в точке», «точка разрыва функции». Изложите классификацию точек разрыва. Продемонстрируйте на рисунках поведение графика функции в точках разрыва
ОТВЕТ:
Функция
f(x) называется непрерывной
функцией
в точке A,
если существует предел
данной функции
при аргументе стремящимся к A
и он равен f(a), т.е.
![]()
Критерий непрерывности функции в точке:
Функция будет непрерывна в точке A тогда и только тогда, когда она будет непрерывна в точке A и справа и слева, т.е. чтобы в точке A существовали два односторонних предела, они были равны между собой и равнялись значению функции в точке A.
Точку В из области определения функции будем называть точкой разрыва функции, если функция не является непрерывной в точке B.
Классификация точек разрыва:
1) Точка разрыва функции называется точкой неопределенности, если не существует правого либо левого одностороннего предела;
2) Если существует оба односторонних предела, но по крайней мере один из них не конечен , то точка разрыва называется точкой бесконечного скачка;
3) Если существует оба односторонних предела, но они не равны между собой , то точка разрыва называется точкой конечного скачка;
4) Если существует оба односторонних предела и они не равны между собой, но не равны значению функции в данной точке, то точка разрыва называется точкой устраненного разрыва.
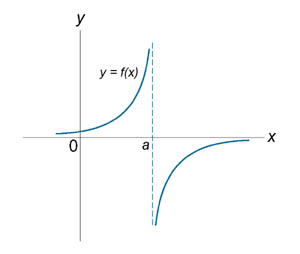 Разрывы
из пунктов 1) и 2) называются разрывами
второго рода, а
из пунктов 3) и 4) разрывами
первого рода.
Разрывы
из пунктов 1) и 2) называются разрывами
второго рода, а
из пунктов 3) и 4) разрывами
первого рода.
Имеет разрыв при x = a.
Дайте определение понятия «производная функции в точке». Сформулируйте правила дифференцирования алгебраических функций. Продемонстрируйте их применение
ОТВЕТ:
Пусть
в некоторой окрестности
точки
![]() определена функция
определена функция
![]() Производной
функции f
в точке x0
называется предел,
если он существует,
Производной
функции f
в точке x0
называется предел,
если он существует,
![]()
Правила дифференцирования алгебраических функций:
Если C — постоянное число и f=f(x), g=g(x) — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
1. C' = 0; → 5’=0
2. x' = 1; → x’=1
3. (f + g)’=f’+g’; → (x2 + y4)’= 2x + 4y3
4. (fg)’=f’g+fg’; → (x3·y5)’= 3x2·y5+x3·5y4
5. (C·f)’=C·f’; → (5x3)’= 5·3x2= 15x2
6. (f/g)’=(f’g – fg’)/g2, (g≠0); → (x4/y3)’=(4x3·y3 – x4·3y2)/y6
7. (C/g)’= -(C·g’/g2), (g ≠ 0). → (1/x)’= -(1·x’/x2)= -(1/x2)
Если функция задана параметрически:
![]() ,
то
,
то
![]() .
.
Дайте определение понятия «производная функции в точке». Сформулируйте правила дифференцирования сложной функции. Продемонстрируйте их применение
ОТВЕТ:
Пусть в некоторой окрестности точки определена функция Производной функции f в точке x0 называется предел, если он существует,
Правила дифференцирования сложной функции:
![]()
Пример: y=(x3+2x)4
y=u4; u=x3+2x
(u4)’=4·u3·u’
y’=4(x3+2x)3·(x3+2x)’= 4(x3+2x)3·(3x2+2).
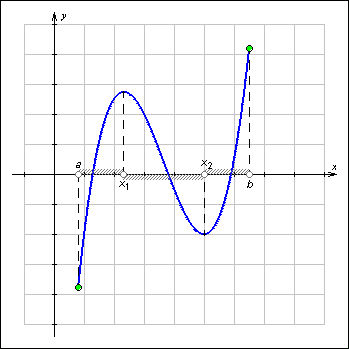
Назовите и объясните виды монотонностей функции. Сформулируйте условия возрастания и убывания функции на промежутке и продемонстрируйте их на примере функции
ОТВЕТ:
(Строго) возрастающая или убывающая функция называется (строго) монотонной.
Пусть дана функция f: M c R→R. Тогда:
-
функция f
называется возрастающей
на M,
если:
![]() .
.
-
функция f
называется строго
возрастающей
на M,
если:
![]() .
.
-
функция f
называется убывающей
на M,
если:
![]() .
.
-
функция f
называется строго
убывающей
на M,
если:
![]() .
.
Условие монотонности функции:
Пусть функция f Є C((a, b)) непрерывна на (a, b), и имеет в каждой точке x Є (a, b) производную f'(x). Тогда
f
возрастает на (a,b)
тогда и только тогда, когда
![]()
f
убывает на (a,b)
тогда и только тогда, когда
![]()
ГРАФИК:
Дайте определение понятий «функция двух переменных», «частные производные функции двух переменных». Запишите формулу нахождения полного дифференциала. Изложите правила нахождения частных производных и продемонстрируйте их на примере функции
ОТВЕТ:
Понятие
функции
двух переменных,
а также понятия ее предела и непрерывности
устанавливаются аналогично тому, как
это делается для функции одного
переменного. Частные производные функции
z=f(x, у) определяются равенствами:
![]()
где
Δхz
и Δуz
- частные приращения функции, получаемые
ею, когда изменяется лишь один из
аргументов. Частные производные по
каждому переменному отыскиваются по
правилам, известным для функции одного
аргумента, поскольку другой аргумент
остается постоянным. Частные дифференциалы
выражаются формулами:
![]()
Полное
приращение функции: Δz=f(x+Δx; y+Δy)-f(x, y).
Пусть в окрестности фиксированной точки
(х, у) при переходе от нее к любой другой
точке (x+Δx; y+Δy) полное приращение Δz
функции z=f(x, у) можно представить в виде:
![]()
где А и В - постоянные (соответствующие фиксированной точке), а, α, β - бесконечно малые при Δх, Δy→0; тогда величина АΔх+ВΔу называется полным дифференциалом функции z в точке (х, у) и обозначается через dz. Полный дифференциал функции z есть часть ее полного приращения Δz, линейная относительно приращений Δх, Δу независимых переменных. При малых Δх, Δу верно приближенное равенство dz≈Δz.
Из существования полного дифференциала следует существование частных производных, причем
![]()
поэтому
![]()
Достаточное условие существования полного дифференциала dz в точке (х, у): функция г имеет в окрестности точки (х, у) частные производные ∂z/∂х, ∂z/∂y, непрерывные в самой точке (х, у). Функция, имеющая в данной точке полный дифференциал, называется дифференцируемой в этой точке.
Производные
высших, порядков определяются так же,
как для функции одного переменного.
Производных второго порядка имеется
четыре:
![]() ,
но если смешанные производные непрерывны,
то они не зависят от порядка
дифференцирования, т. е.
,
но если смешанные производные непрерывны,
то они не зависят от порядка
дифференцирования, т. е.
![]() так
что остается лишь три различных
производных. Различных производных
третьего порядка оказывается четыре:
так
что остается лишь три различных
производных. Различных производных
третьего порядка оказывается четыре:
![]()
Вообще
различных производных порядка n имеется
n+1. Если z=f(u, v), где u=φ(х, у), v=ψ(x, у), т. е.
если z есть сложная функция от х, у, причем
все эти функции дифференцируемы в
рассматриваемой точке, то частные
производные отыскиваются по формулам:
![]()
![]()
Если
z=f(u, v), где u=φ(t), v=ψ(t), т. е. если z есть
сложная функция одного аргумента t, то
производная от z по t отыскивается по
формуле:
![]()
Из
формулы для полного дифференциала
видно, что
![]() где
где
![]()
Однако не всякое выражение такого вида является полным дифференциалом некоторой функции, но лишь такое, в котором выполняется условие ∂P/∂y=∂Q/∂x.
Пример: Z(x; y)=2x3y2+3xy3
Z’(x)= = 2y2(x3)’+3y3(x)’=2y23x2+3y3= 6y2x2+3y3
Z’(y)= = 2x3(y2)’+3x(y3)’= 2x32y+3x3y2= 4x3y+9xy2
Z’’(xx)= = (Z’(x))’x= (6y2x2+3y3)’= 6y22x+0=12y2x
Z’’(xy)= = (6y2x2+3y3)’y= 6x22y+9y2
Z’’(yx)= = (4x3y+9xy2)’= 12x2y+9y2
Z’’(yy)= = (4x3y+9xy2)’= 4x3+18xy.
Дайте определение понятий «первообразная функции», «неопределенный интеграл». Изложите основные свойства неопределенного интеграла. Изложите таблицу неопределенных интегралов и продемонстрируйте ее на примере
ОТВЕТ:
|
Функция F(x) называется первообразной функции f(x), если: F’(x)=f(x).
Например: функция F=x3/3 является первообразной функции f(x)=x2, в чем можно убедиться, поставив эти функции в определение первообразной.
Множество
всех первообразных некоторой функции
f(x)
называется неопределенным
интегралом
функции
f(x)
и обозначается как
![]()
Таким
образом, если F
- некоторая частная первообразная, то
справедливо выражение:
![]()
где С - произвольная постоянная.
Свойства неопределенного интеграла:
f и g - функции переменной x; F - первообразная функции f, а, k, C - постоянные величины.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
Таблица основных неопределённых интегралов:
![]()
![]()
![]()
![]()
Пример:
![]()
![]()
Пример:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
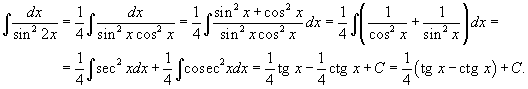
![]()
![]()