9. Дайте определение понятия «определитель третьего порядка». Запишите и объясните формулу его вычисления. Продемонстрируйте на примерах вычисление определителей

ОТВЕТ:

Определителем 1-го порядка квадратной матрицы А размерности 1×1 является единственный элемент этой матрицы |А| (определитель матрицы А).

Пример: А_1×1

|А|=det А=|а₁₁|=а₁₁.

(det - детерминант)

Определителем 3-го порядка квадратной матрицы А размерности 3×3 (А_3×3) называется величина, определяемая соотношением:

|А|=detА= = (а₁₁·а₂₂·а₃₃+а₁₃·а₂₁·а₃₂+а₁₂·а₂₃·а₃₁)-(а₁₃·а₂₂·а₃₁+а₁₁·а₂₃·а₃₂+а₁₂·а₂₁·а₃₃).

П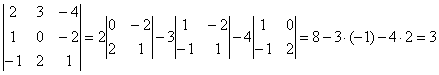 ример:

=(2·0·1+(-1) ·3· (-2)+1· (-4) ·2)-((-4) ·0· (-1)+1·3·1+2·2· (-2))=-2+5=3.

10. Дайте определение понятия «система линейных уравнений». Сформулируйте теорему Крамера. Охарактеризуйте метод решения слау по формулам Крaмера

ОТВЕТ:

Совокупность уравнений:

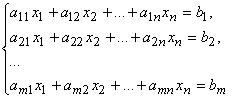
относительна неизвестных x₁, x₂, ..., x_n-1, x_n называется системой линейных алгебраических уравнений (СЛАУ).

Числа a_ij — коэффициенты системы, b_i — правые части системы i = 1, 2, ..., m; j = 1, 2, ..., n.

Совокупность значений неизвестных, удовлетворяющая всем уравнениям системы, называется решением системы.

Система, имеющая хотя бы одно решение, называется совместной. Система, у которой нет решений, называется несовместной.

Каждое решение совместной системы называется частным решением. Совокупность всех решений совместной системы называется общим решением.

Если среди правых частей b_i системы есть хоть одна, отличная от нуля, то система называется неоднородной системой линейных уравнений.

Если все правые части системы равны нулю, то система называется однородной.

Теорема Крамера: Система из n уравнений с n неизвестными в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам: x_i = Δ_i/Δ, где Δ=|A|,  а Δ_i – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов b_i.

П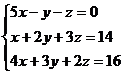 ример:

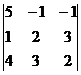=  =(20-3-12)-(-8+45-2)=-30; 1 = 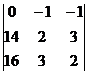 =(0-42-48)-(-32+0-28)=-30.

х1=Δ1/Δ=1; 2 = 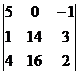 =(140-16+0)-(-56+240+0)=-60.

x2=Δ2/Δ=2; 3=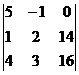  =(160+0-56)-(0+210-16)=-90. x3=Δ3/Δ= 3.

Ответ:

11. Дайте определение понятия «система линейных уравнений». Сформулируйте условия применения метода Гаусса. Охарактеризуйте метод решения слау методом Гаусса

ОТВЕТ:

Совокупность уравнений:

относительна неизвестных x₁, x₂, ..., x_n-1, x_n называется системой линейных алгебраических уравнений (СЛАУ).

Числа a_ij — коэффициенты системы, b_i — правые части системы i = 1, 2, ..., m; j = 1, 2, ..., n.

Совокупность значений неизвестных, удовлетворяющая всем уравнениям системы, называется решением системы.

Система, имеющая хотя бы одно решение, называется совместной. Система, у которой нет решений, называется несовместной.

Каждое решение совместной системы называется частным решением. Совокупность всех решений совместной системы называется общим решением.

Если среди правых частей b_i системы есть хоть одна, отличная от нуля, то система называется неоднородной системой линейных уравнений.

Если все правые части системы равны нулю, то система называется однородной.

Метод Гаусса – это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.

П ример:

x +  y - 3z = 2,

3x - 2y +  z = - 1,

2x +  y - 2z = 0.

Решение. Выпишем расширенную матрицу данной системы:

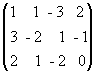
и произведем следующие элементарные преобразования над ее строками:

а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2:

 ~ ;

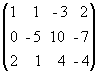б) третью строку умножим на (-5) и прибавим к ней вторую:

.

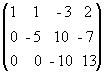В результате всех этих преобразований данная система приводится к треугольному виду:

x + y - 3z = 2,

   -5y + 10z = -7,

         -10z = 13.

Из последнего уравнения находим z= -1,3.

Подставляя это значение во второе уравнение, имеем y= -1,2.

Далее из первого уравнения получим x= -0,7.