43. Дайте определение понятия «граф», опишите его простейшие свойства. Приведите примеры решения задач с использованием графов

ОТВЕТ:

вершины

ребра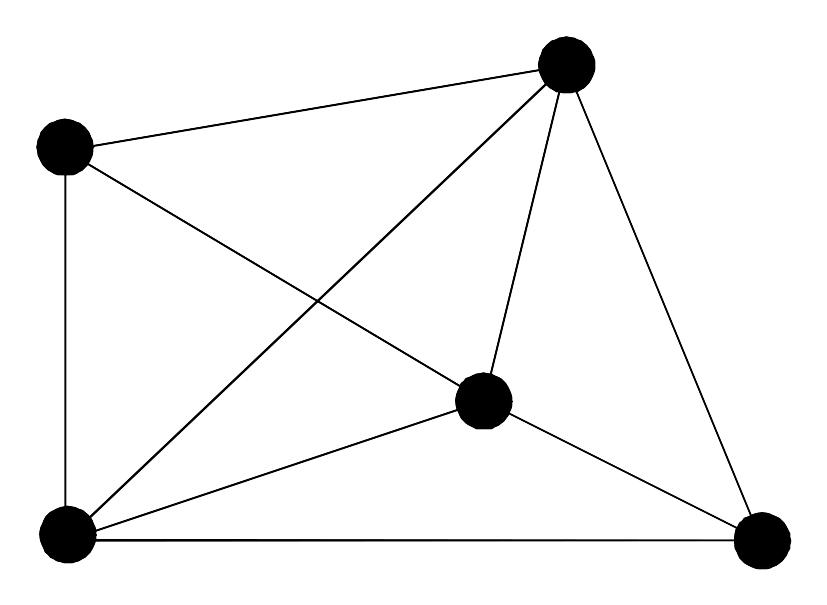

Графом называется совокупность множеств вершин и ребер.

V – множество точек – вершины;

X – множество линий – ребра;

v – номер вершины;

{v, w} – обозначение ребра;

{v, v} – петли.

Свойства графа:

Граф G называется деревом, если он является связным и не имеет циклов. Граф G называется лесом, если все его компоненты связности – деревья.

Деревья обладают следующими свойствами:

1) Граф G есть дерево;

2) Граф G является связным и не имеет простых циклов;

3) Граф G является связным и число его ребер ровно на 1 меньше числа вершин;

4)  две различные вершины графа G можно соединить единственной (и при этом простой) цепью;

5) Граф G не содержит циклов, но, добавляя к нему любое новое ребро, получаем ровно один и притом простой цикл.

Задача: Между девятью планетами солнечной системы установлено космическое сообщение. Рейсовые ракеты летают по следующим маршрутам: Земля – Меркурий; Плутон – Венера; Земля – Плутон; Плутон – Меркурий; Меркурий – Венера; Уран – Нептун; Нептун – Сатурн; Сатурн – Юпитер; Юпитер – Марс и Марс – Уран. Можно ли долететь на рейсовых ракетах с Земли до Марса?

Решение: Нарисуем схему условия: планеты изобразим точками, а маршруты ракет – линиями.

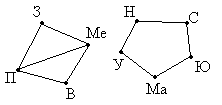
Теперь сразу видно, что долететь с Земли до Марса нельзя.

44. Дайте определение понятия «событие» (достоверное событие, невозможное событие, элементарные события). Опишите действия над событиями (событие А влечет за собой событие В, равенство событий, сумма событий, произведение событий, несовместные события, дополнение к событию, разность событий)

ОТВЕТ:

Событие – всё, что может произойти (наступить) или может не произойти (не наступить).

Достоверное событие – это событие, которое в результате наблюдения обязательно происходит.

Невозможное событие – это событие, которое в результате испытания обязательно не наступит.

Элементарные события – это подмножество пространства исходов случайного эксперимента, которое состоит только из одного элемента.

Действия над событиями:

1. Если при всяком испытании, при котором происходит событие А, происходит и событие B, то событие А называется частным случаем события B.

Говорят также, что А влечет за собой B и пишут: или .

Например, при бросании игральной кости событие А, состоящее в появлении двух очков, есть частный случай

события B, состоящего в появлении четного числа очков.

Если А влечет за собой B, а B влечет за собой А, то эти события равносильны, так как они вместе наступают или вместе не наступают.

2. Равенство (эквивалентность) событий: А = В, если А В и В А.

3. Событие (А или B), т. е. событие, состоящее в наступлении хотя бы одного из событий А и B, называется суммой событий А и B и обозначается через: А+В.

4. Событие (А и B), т. е. событие, состоящее в наступлении обоих событий А и B, называется произведением событий А и B и обозначается через: А·В.

5. Два события A и B называются несовместимыми, если они не могут появиться совместно, т. е. если AB = H.

Например, при бросании игральной кости появление 1 очка и появление 2 очков представляют несовместимые события.

Ясно, что противоположные события являются несовместимыми. Если B = A₁ + A₂ + ... + A_n и события A попарно несовместимы, т. е. каждое несовместимо с остальными: A_i A_k = H при i № k, то говорят, что событие B подразделяется на частные случаи A₁ , A₂ , ... , A_n .

Например, событие B, состоящее в выпадении нечетного числа очков, подразделяется на частные случаи E₁, E₃, E₅, состоящие соответственно в выпадении 1, 3 и 5 очков.

6. Дополнение к событию: → _.

7. Событие (А и ), состоящее в том, что A происходит, а B не происходит, называется разностью событий А и B и обозначается через: А – В.