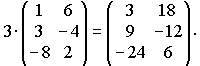Экзаменационные вопросы

по дисциплине «Математика»

для учащихся 3-го курса заочной формы обучения

специальности 2-27 01 01 «Экономика и организация производства».

1. Дайте определение понятий «объединение множеств», «пересечение множеств». Изобразите объединение, пересечение множеств а и в с помощью кругов Эйлера

ОТВЕТ:

Объединение множеств А и В называется множество всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств А, В. Объединение обозначается: А+В. Например: Х={1,2,3,4} У={2,4,6} объединением {1,2,3,4,6}.

И зобразим объединение множеств А и В с помощью кругов Эйлера:

П ри объединении могут встретиться следующие 6 случаев:

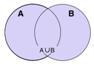
Пересечением А и В называется множество всех тех и только тех элементов множества А, которые не принадлежат В. Пересечение обозначается: А*В. Например: Х={1,2,3,4} У={2,4,6} пересечением {2,4}.

Изобразим пересечение множеств А и В с помощью кругов Эйлера:

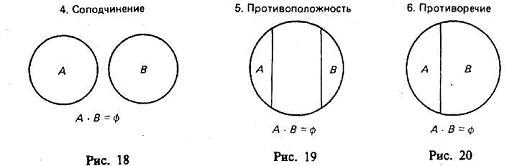
П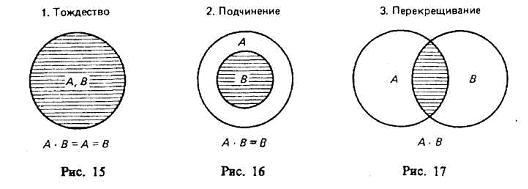 ри объединении могут встретиться следующие 6 случаев:

2. Дайте определение понятий «разность множеств», «дополнение множества». Изобразите разность и дополнение множеств а и в с помощью кругов Эйлера

ОТВЕТ:

Разностью множеств А и В называется множество всех тех элементов множества А, которые не принадлежат множеству В. Разность обозначается: А-В. Например: Х={1,2,3,4} У={2,4,6} разность {1,3}.

Изобразим разность множеств А и В с помощью кругов Эйлера:

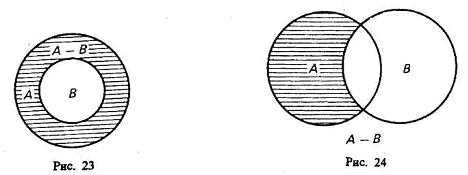
Дополнение множества А называется множество всех элементов, которые не входят во множество А.

Изобразим дополнение множеств А и А’ с помощью кругов Эйлера:

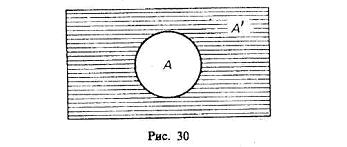
3. Дайте определение комплексного числа (его действительной и мнимой части). Запишите комплексное число в алгебраической форме. Дайте определение равных комплексных чисел. Назовите и опишите операции на множестве комплексных чисел (сложение, умножение, возведение в целую степень) и их свойства

ОТВЕТ:

Комплексным числом называется выражение вида x+iy; где x и y – любые действительные числа, i – специальное число, которое называется мнимой единицей.

Комплексное число в алгебраической форме: z = x+iy.

Действительное число x называется действительной частью комплексного числа z, действительная часть обозначается x = Re z. Действительное число y называется мнимой частью комплексного числа z, мнимая часть обозначается y = Im z.

Сложение комплексных чисел:

z1 + z2 = (x1 + iy1) + (x2 + iy2) = (x1 + x2) + i(y1 + y2),

то есть при сложении комплексных чисел складываются их действительные и мнимые части.

Пример: (1 + i) + (2 – 3i) = 1 + i + 2 –3i = 3 – 2i;

Основные свойства сложения:

1) z1 + z2 = z2 + z1;

2) z1 + z2 + z3 = (z1 + z2) + z3 = z1 + (z2 + z3);

3) z1 – z2 = z1 + (– z2);

4) z + (–z) = 0.

Умножение (возведение в целую степень) комплексных чисел:

z1∙z2 = (x1 + iy1)∙(x2 + iy2) = x1x2 + x1iy2 + iy1x2 + i2y1y2 = (x1x2 – y1y2) + i(x1y2 + y1x2),

то есть умножение комплексных чисел в алгебраической форме проводится по правилу алгебраического умножения двучлена на двучлен с последующей заменой i²= –1 и приведением подобных по действительным и мнимым слагаемым.

Примеры:

1) (1 + i)∙(2 – 3i) = 2 – 3i + 2i – 3i² = 2 – 3i + 2i + 3 = 5 – i;

2) (1 + 4i)∙(1 – 4i) = 1 – 4i + 4i – 16i = 1 + 16 = 17;

3) (2 + i)² = 4 + 4i + i² = 3 + 4i.

Основные свойства умножения:

1) z1z2 = z2z1 — коммутативность;

2) z1z2z3 = (z1z2)z3 = z1(z2z3) — ассоциативность;

3) z1(z2 + z3) = z1z2 + z1z3 — дистрибутивность относительно сложения;

4) z0 = 0; z1 = z.

4. Дайте определение комплексного числа (его действительной и мнимой части). Запишите комплексное число в алгебраической форме. Назовите и опишите операции на множестве комплексных чисел (вычитание, деление) и их свойства

ОТВЕТ:

Комплексным числом называется выражение вида x+iy; где x и y – любые действительные числа, i – специальное число, которое называется мнимой единицей.

Комплексное число в алгебраической форме: z = x+iy.

Действительное число x называется действительной частью комплексного числа z, действительная часть обозначается x = Re z. Действительное число y называется мнимой частью комплексного числа z, мнимая часть обозначается y = Im z.

Вычитание комплексных чисел:

z1 + z2 = (x1 + iy1) + (x2 + iy2) = (x1 + x2) + i(y1 + y2),

то есть при вычитании комплексных чисел вычитаются их действительные и мнимые части.

Пример: (1 + i) – (2 – 3i) = 1 + i – 2 – (–3i) = 4i – 1.

Основные свойства сложения:

1) z1 – z2 = – (z2 – z1);

2) z1 – z2 – z3 = (z1 – z2) – z3 = z1 – (z2 + z3);

3) –z + z = 0.

Деление комплексных чисел:

Деление — это обратная умножению операция, поэтому, если zz2 = z1 и z2  0, то z=z1/z2.

При выполнении деления в алгебраической форме числитель и знаменатель дроби умножаются на число, комплексно сопряженное знаменателю: .

Пример:

.

Основные свойства деления:

1) z1/z2=z1*(1/z2).

5. Дайте определение понятий «матрица», «размерность матрицы», «элемент матрицы», «индексы элемента матрицы». Назовите виды матриц и опишите линейные операции над матрицами (сложение матриц, умножение матрицы на число)

ОТВЕТ:

Матрица – это таблица, которая состоит из m – строк и n – столбцов, элементами которой являются числа:

.

Матрицы обозначаются заглавными буквами, например, матрица А:

А= .

Количество строк (m) и столбцов (n) матрицы задают размер матрицы. Следовательно, размерность нашей матрицы: m×n.

Элементами матрицы являются числа, которые обозначаются строчными буквами с соответствующими индексами элемента матрицы, т.е. a_ij.

Виды матриц:

1. Вектор-строка: (1×n);

2. Вектор-столбец: (m×1);

3. Квадратная матрицы: (n×n);

4. Нулевая матрица: матрица, элементами которой являются нули.

Операции над матрицами:

- сложение матриц: суммой двух матриц А и В одной и той же размерности называется матрица С, элементы которой рассчитываются по правилу: c_ij= a_ij+b_ij.

С = А+В → c_ij= a_ij+b_ij.

П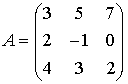 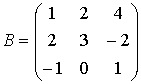ример:

      

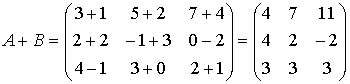
- умножение матрицы на число: произведение матрицы А на число λ называется матрица С, элементы которой рассчитываются по правилу: c_ij= λ·a_ij.

А, λєR, C → c_ij= λ·a_ij.

Пример: