Лабораторная работа № 4 Исследование эквивалентности преобразований структурных схем линейных сау

1. Цель лабораторной работы

Целью лабораторной работы является закрепление теоретических знаний о временных характеристиках типовых линейных звеньев путем экспериментального исследования с помощью измерительных средств виртуальной электронной лаборатории на персональном компьютере на базе программы VisSim.

2. Задачи лабораторной работы

К задачам лабораторной работы относятся:

1. Освоение методов экспериментального исследования и анализа линейных систем с помощью измерительных средств виртуальной электронной лаборатории на персональном компьютере на базе программы VisSim.

2. Исследование эквивалентности преобразований структурных схем линейных САУ при последовательном и параллельном соединении звеньев, а также для систем с обратной связью.

3. Исследование эквивалентности последовательных преобразований сложной структурной схемы линейной САУ.

3. Краткие теоретические сведения.

3.1. Методы преобразования структурных схем

1. Последовательное соединение звеньев

Для простоты возьмем три последовательно соединенных звена.

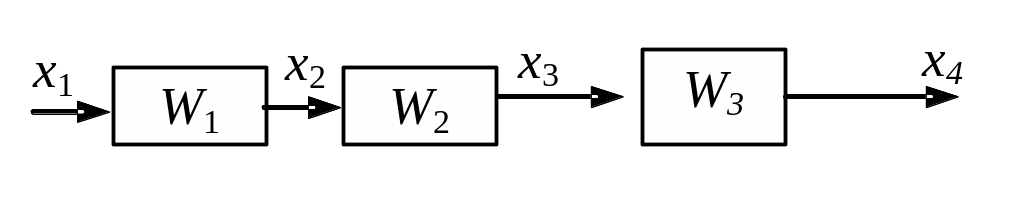
Найдем эквивалентную передаточную функцию этого соединения. Для каждого звена в операторной форме можно записать:

;

Выполним последовательную подстановку^

По определению передаточная функция равна:

Обобщая этот результат на n звеньев, получим:

EMBED Word.Picture.8

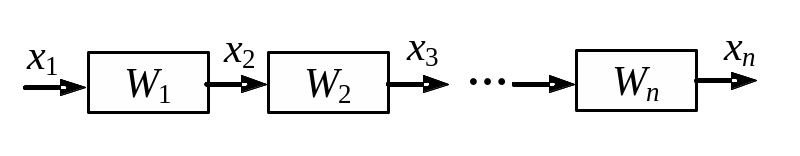
Таким образом, передаточная функция системы последовательно соединенных звеньев равна произведению передаточных функций отдельных звеньев

2. Параллельное соединение звеньев

Для простоты возьмем три параллельно соединенных звена

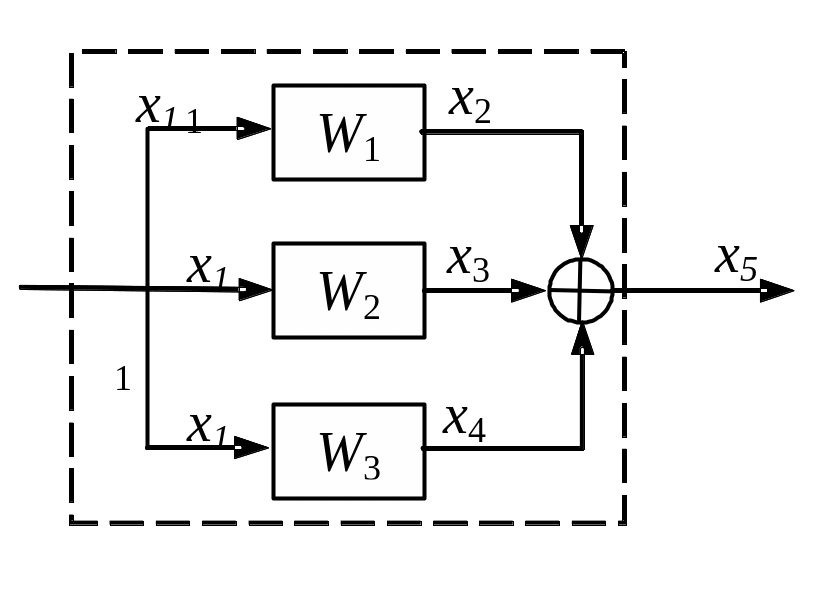
Для каждого звена в операторной форме можно записать:

; ;

Откуда выходной сигнал равен:

По определении. передаточная функция равна:

Обобщая этот результат на n звеньев, получим:

.

Таким образом, передаточная функция системы параллельно соединенных звеньев равна сумме передаточных функций отдельных звеньев.

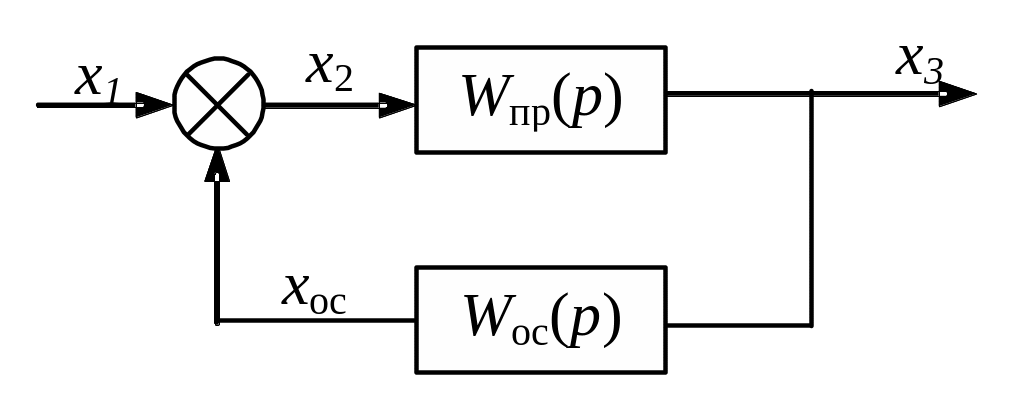
3. Система с обратной связью

Обратной связью называют передачу сигнала с выхода звена на его вход, где сигнал обратной связи алгебраически суммируется с внешним сигналом. Структурная схема соединения с обратной связью изображена на рис. 1.

Если х₂ = х₁ + x_ос, то связь называется положительной, если же х₂ = х₁  x_ос, то – отрицательной.

Для вывода передаточной функции соединения с положительной обратной связью выходные сигналы для каждого звена в операторной форме записываются как:

.

Исключая из полученной системы X₂(p) и X_ос(p), получают

;

,

о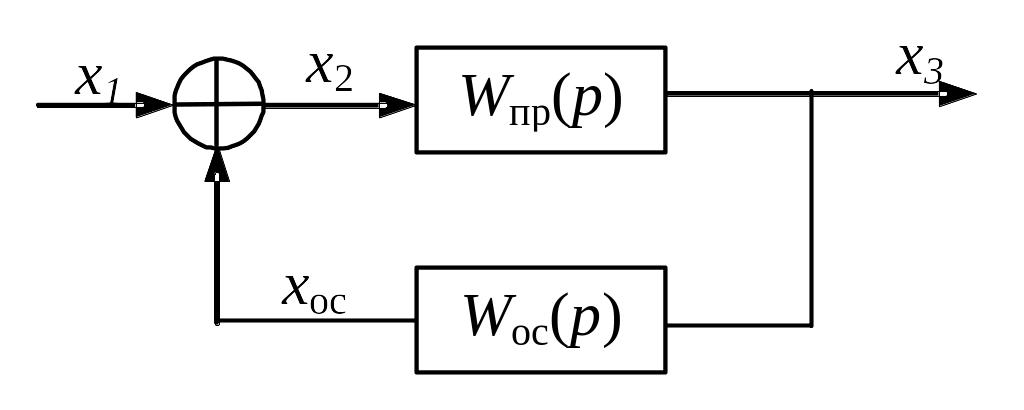 ткуда передаточная функция соединения с положительной обратной связью имеет вид:

Рис. 1 Структурная схема САУ с положительной обратной связью

. (1)

Для соединения с отрицательной обратной связью передаточная функция выводится аналогичным образом и определяется в окончательном виде выражением

. (2)

На практике наиболее распространенными являются системы с отрицательной обратной связью, к ним относятся, например, все одноконтурные системы автоматического регулирования, причем в прямой цепи расположен объект, а в обратной – регулятор.