Лабораторная работа № 3

Исследование частотных характеристик типовых линейных звеньев (апериодическое звено первого порядка, колебательное звено, идеальное интегрирующее звено, идеально дифференцирующее звено)

1. Цель лабораторной работы

Целью лабораторной работы является закрепление теоретических знаний о частотных характеристиках типовых линейных звеньев путем экспериментального исследования с помощью измерительных средств виртуальной электронной лаборатории на персональном компьютере на базе программы VisSim.

2. Задачи лабораторной работы

К задачам лабораторной работы относятся:

1. Освоение методов экспериментального исследования и анализа линейных систем с помощью измерительных средств виртуальной электронной лаборатории на персональном компьютере на базе программы VisSim.

2. Построение и анализ частотных характеристик апериодическое звена первого порядка, колебательного звена, идеального интегрирующего звена, идеального дифференцирующего звена.

3. Краткие теоретические сведения.

3.1.Апериодическое звено 1-го порядка.

Передаточная функция звена равна:

W (р) = =

Частотная передаточная функция получается подстановкой в это уравнение вместо оператора Лапласа р произведение j :

где U₁( ) = К, V₁( ) = 0, U₂( ) = 1, V₂( ) = Т ,

Это выражение можно преобразовать к виду:

=

где U( ) = , V( ) =

Годограф АФХ для  > 0 целиком лежит в четвертом квадранте и представляет собой полуокружность диаметром k с центром в точке , которая описывается уравнением

.

АЧХ получается следующим образом:

A( ) = =

ФЧХ получается так:

Графики частотных характеристик имеют вид:

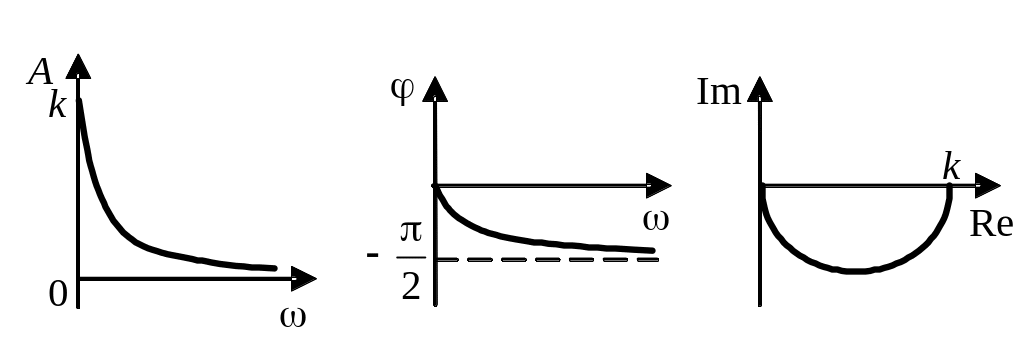
Амплитудно-частотная характеристика апериодического звена первого порядка на нулевой частоте равна коэффициенту усиления k, с увеличением частоты она монотонно уменьшается, асимптотически стремясь к нулю.

Фазовая частотная характеристика при увеличении частоты от 0 до  изменяется от 0 до .

Из АЧХ видно, что колебания малых частот ( < 1/Т) «пропускаются» данным звеном с отношением амплитуд выходной и входной величии, близким к статическому коэффициенту передачи звена К. Колебания больших частот ( >1/Т) проходят с сильным ослаблением амплитуды, т. е. «плохо пропускаются» или практически совсем «не про­пускаются» звеном. Чем меньше постоянная времени Т, т. е. чем меньше инерционность звена, тем более вытянута АЧХ А ( ) вдоль оси частот, или, как говорят, тем шире полоса пропускания частот _п данного звена:

_п = 1/T – (-1/T) = 2/T

ЛАЧХ строится по выражению:

L( ) = 20lg A( ) = 20lg

Наиболее просто, практически без вычислительной работы, строится так называемая асимптотическая ЛАЧХ. На стандартной сетке проводится вертикальная прямая через точку с частотой, называемой сопрягающей частотой = 1/Т,. Для частот меньших, чем сопрягающая, т. е. при < 1/Т, можно пренебречь вторым слагаемым под корнем в выражении L( ). Тогда левее сопрягающей частоты можно заменить L( ) приближенным выражением L( ) 20lg К (при < 1/Т), которому соответствует прямая линия, параллельная оси частот (прямая ав ) и являющаяся первой асимптотой.

Для частот больших, чем сопрягающая ( >1/Т), в выражении L( ) можно пренебречь под корнем единицей по сравнению с ²Т². Тогда выражение L( ) будет иметь приближенное значение:

L( ) 20lg К/ Т при >1/Т

которому соответствует прямая с отрицательным наклоном 20 дб/дек, являющаяся второй асимптотой. Ломанная линия называется асимптотической ЛАЧХ . Действительная ЛАЧХ (показанная пунктиром) будет несколько отличаться от асимптотической, причем наибольшее отклонение будет при = 1/Т и равно приблизительно 3дб, т.к.

L(1/Т) = 20lg К/ = 20lg К – 3,03 дб

что в линейном масштабе соответствует отклонению в раз. На всем осталь­ном протяжении влево и вправо от сопрягающей частоты действительная ЛАЧХ. будет отличаться от асимптоти­ческой менее чем на 3 дб. Поэтому во-многих практических расчетах доста­точно ограничиться построением асимп­тотической ЛАЧХ.

3.2. Идеальное интегрирующее звено.

Передаточная функция звена равна:

Частотная передаточная функция получается подстановкой в это уравнение вместо оператора Лапласа р произведение j :

=

где U( ) = 0, V( ) = - К/

При = 0, , при = ,

АФХ представляет собой прямую, совпадающую с отрицательной полуосью мнимой оси..

Модуль частотной переда­точной функции А( ) = = = представляет собой гиперболу .

ФЧХ имеет вид:

( )= arctg = arctg = arctg-  = -90⁰

График частотных характеристик имеют вид

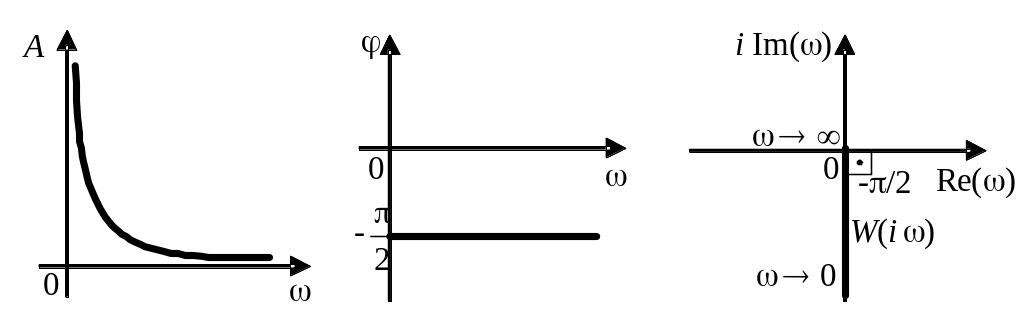
ЛАЧХ имеет вид:

L( ) = 20lg A( ) = 20lg

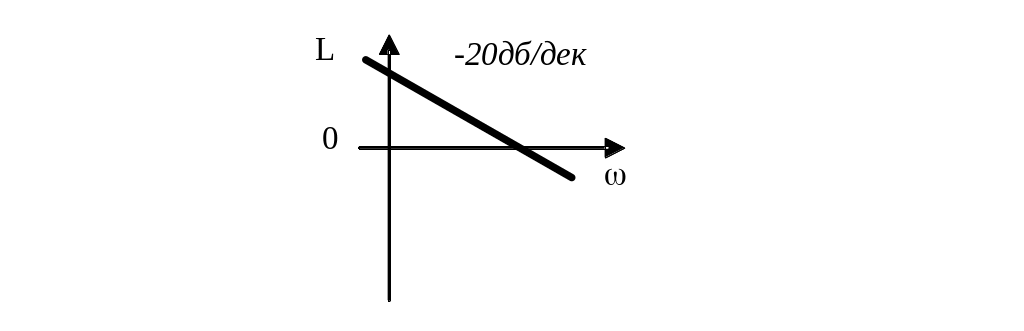
График ЛФЧХ имеет вид:

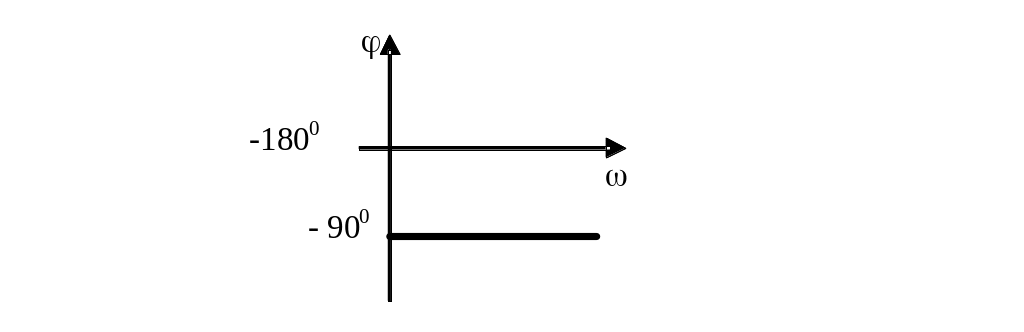
3.3.Идеальное дифференцирующее звено.

Передаточная функция звена равна:

W (р) = = Кр

Частотная передаточная функция получается подстановкой в это уравнение вместо оператора Лапласа р произведение j :

АЧХ получается следующим образом:

А ( ) = = = К

График представляет собой прямую.

ФЧХ получается так:

( )= = = = 90⁰

Графики частотных характеристик имеют вид:

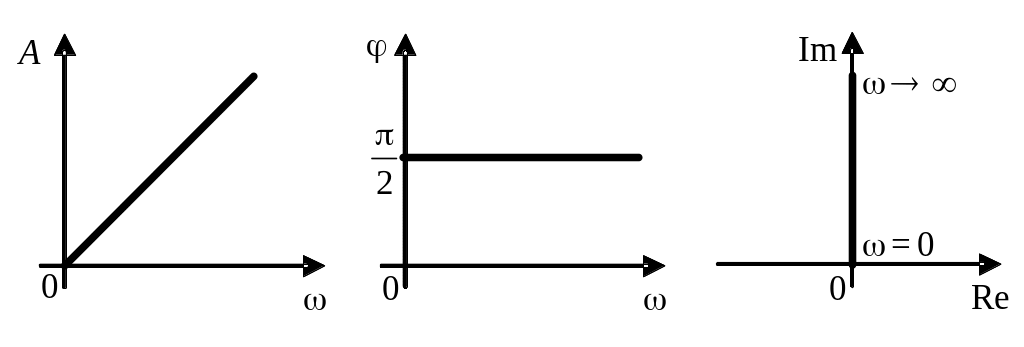
Логарифмические характеристики имеют вид:

L( ) = 20lg A( ) = 20lg К

которому соответствует прямая с положительным наклоном 20 дб/дек.

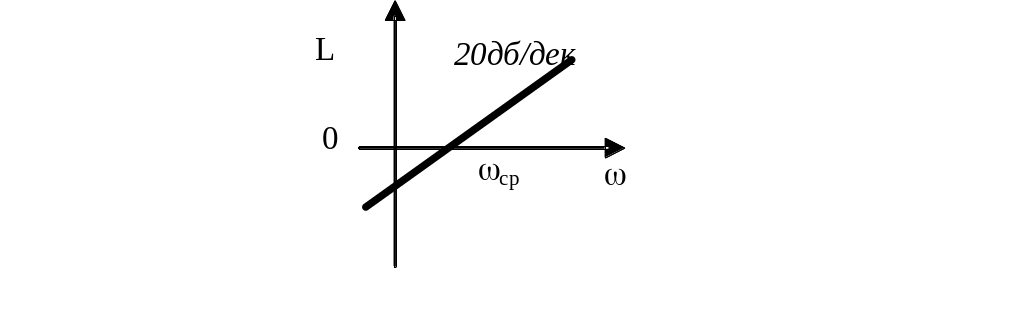
ЛФЧХ имеет вид:

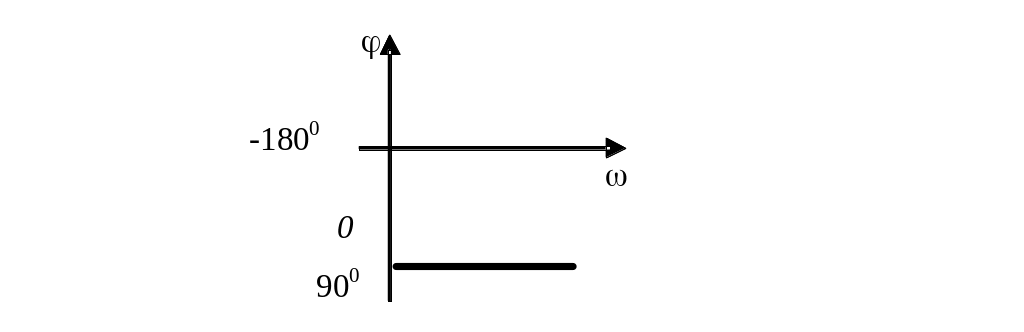
3.4. Колебательное звено.

Передаточная функция звена имеет вид:

Частотная передаточная функция имеет вид:

;

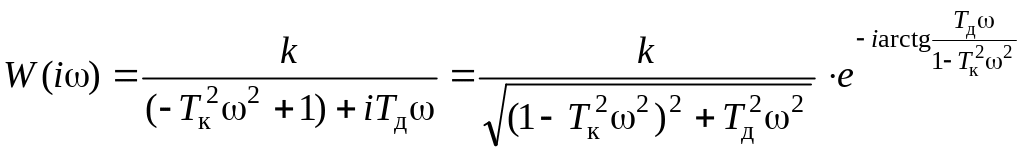– АЧХ

;

– ФЧХ

. )