Множество z целых чисел

Определение 2.4. Натуральные, отрицательные натуральные числа и ноль образуют множество целых чисел (множество Z).

Сумма, произведение и разность целых чисел является целым числом, а частное — не всегда. Множество натуральных чисел является подмножеством множества целых чисел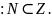

Наиболее употребляемыми в настоящее время позиционными системами являются:

• 2 — двоичная (в дискретной математике, информатике, программировании);

• 8 — восьмеричная;

• 10 — десятичная (используется повсеместно);

• 12 — двенадцатеричная римская(счёт дюжинами);

• 16 — шестнадцатеричная (используется в программировании, информатике);

• 60 — шестидесятеричная вавилонская (единицы измерения времени, измерение углов и, в частности, координат, долготы и широты).

Множество q рациональных чисел

Определение 2.5. Рациональными числами называются числа вида , где m —целое, n — натуральное, m и n взаимно простые. Множество рациональных чисел обозначается Q.

Множество целых чисел является подмножеством рациональных чисел, т.к. любое число m можно рассматривать как рациональное, представив его в виде . Сумма, произведение, разность, частное рациональных чисел (при ненулевом знаменателе) является числом рациональным.

Всякое рациональное число можно представить в виде десятичное дроби, конечной или периодической. И наоборот, любая конечная или периодическая десятичная дробь может быть записана в виде простой дроби.

Пример 2.3. ; ; .

Последние две десятичные дроби — бесконечные периодические. Перевод периодической десятичной дроби в простую поясним на примере.

Пример 2.4. Записать в виде простой дроби 0,(6).

Периодическую дробь 0,(6) обозначим за x: 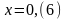, тогда . Легко заметить, что . Решая это уравнение, получаем: или .

Определение 2.6. Целой частью числа называется наибольшее целое число, не превосходящее данное.

Определение 2.7. Дробной частью числа называется разность между числом и его целой частью. Она строго меньше единицы. Множество всех рациональных чисел счетно.

Множество j иррациональных чисел

Определение 2.8. Иррациональным числом называется бесконечная непериодическая десятичная дробь (множество J).

Примерами иррациональных чисел являются и т. д. Заметим, что J Q=Ø. Иррациональное число нельзя представить в виде простой дроби или в виде конечной десятичной дроби. Заданное бесконечной непериодической дробью иррациональное число определяет две последовательности конечных (рациональных) десятичных дробей, называемых десятичными приближениями по недостатку и по избытку. Например, для можно написать:

В инженерных расчетах при замене иррациональных чисел их рациональными приближениями достаточно во всех вычислениях брать на один знак больше, чем требуется в результате, и затем округлить результат.

Множество r действительных чисел

Определение 2.9. Все рациональные и иррациональные числа образуют множество действительных (вещественных) чисел.

В множестве действительных чисел всегда выполнимы сложение, вычитание, умножение, деление (не на ноль), возведение в любую действительную степень положительного числа, извлечение корня нечетной степени из отрицательного числа. Во множестве действительных чисел невозможно извлечение корня четно степени из отрицательного числа.

Множество всех действительных чисел не является счетным.