Множество n натуральных чисел

Числа 1, 2, 3, 4, 5,…, использующиеся для счета предметов или для указания порядкового номера предмета, называются натуральными (множество N).

Натуральные числа представляют собой бесконечное множество. Элементы этого множества можно пронумеровать, т. е. каждому элементу сопоставить некоторый номер из множества натуральных чисел так, что различные элементы получают счетные номера. Поэтому множество N следует отнести к разряду счетных множеств.

Для множества натуральных чисел безоговорочно выполнимы только операции сложения, умножения и возведения в степень. Сумма и произведение натуральных чисел будет натуральным числом, а разность и частное — не всегда. При вычитании натуральных чисел может получиться отрицательное число, а при делении — не целое.

Каждое натуральное число, большее единицы, делится по крайней мере на два числа: на 1 и на само себя. Если число не имеет других натуральных делителей, то такое число называется простым, а если у числа есть другие натуральные делители, то оно называется составным. Единица не считается ни простым, ни составным числом. Представление натурального числа в виде произведения простых сомножителей называется факторизацией числа.

Основная теорема арифметики утверждает, что любое натуральное число либо само является простым, либо может быть разложено на произведение простых делителей, причем единственным способом, если не обращать внимания на порядок следования сомножителей. Разложение на множители называется каноническим, если все множители являются простыми и записаны в порядке возрастания. Таким образом, простые числа можно использовать как «элементарные строительные блоки» натуральных чисел.

Общим кратным двух данных натуральных чисел называется наименьшее из чисел, которые делятся на каждое из них.

Для любых двух натуральных чисел всегда найдется общее кратное, поскольку их произведение всегда делится на каждое из двух данных.

Пример 2.1. Найти наименьшее общее кратное чисел 12 и 18.

Для того чтобы найти наименьшее общее кратное двух чисел, нужно первое число 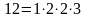умножить на простые множители, входящие в разложение второго числа 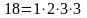и не входящие в разложение первого: .

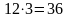Общим делителем двух данных натуральных чисел называется число, на которые делится каждое из них. Для любых двух натуральных чисел всегда найдется общий делитель, поскольку любые два числа всегда делятся на единицу. Если у двух натуральных чисел нет ни одного общего делителя кроме единицы, они называются взаимно простыми.

Пример 2.2. Найти наибольший общей делитель чисел 12 и 18.

Наибольший общий делитель двух чисел 12 и 18 равен 6. Для того чтобы найти наибольший общий делитель двух чисел, нужно перемножить общие простые множители, входящие в разложение и одного и другого числа: .

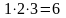Простые числа специального типа

Числа Мерсенна — числа вида 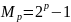, где 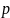 — простое число.

Числа Вудалла — числа вида 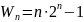, где  — натуральное число.

Числа Прота — числа вид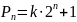а , где  — натуральное число, а 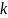нечетно и .

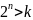Числа Кулдена — числа вида 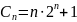, где  — натуральное число. При 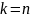числа Кулдена являются частным случаем чисел Прота.

Числа Ферма — числа вида 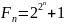, где  — целое положительное число. Числа Ферма являются частным случаем чисел Прота пр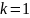и и 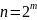. По состоянию на ноябрь 2011 года известно только 5 простых чисел Ферма для 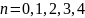и высказана гипотеза, что других простых чисел Ферма нет.

Принято отмечать наибольшие простые числа. Один из рекордов поставил в свое время Эйлер (1707-1783), найдя простое число 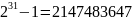. По состоянию на ноябрь 2011 года наибольшим простым числом является 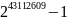. Оно относится к числам Мерсенна и содержит 12 978 189 десятичных цифр.

Алгоритмы определения простых чисел

Небольшую коллекцию простых чисел можно подобрать используя «решето Эратосфена» (III век до н. э.). Для нахождения всех простых чисел не больше заданного числа n, следуя методу Эратосфена, нужно выполнить следующие шаги:

Выписать подряд все целые числа от двух до n (2, 3, 4, …, n). Пусть переменная p изначально равна двум — первому простому числу. Считая от p шагами по p, зачеркнуть в списке все числа от 2p до n кратные p (то есть числа 2p, 3p, 4p, …) Найти первое незачеркнутое число, большее чем p, и присвоить значению переменной p это число. Повторять шаги 3 и 4 до тех пор, пока не станет больше, чем n Теперь все не зачеркнутые числа в списке — простые.

Есть и более современный способ определения простых чисел. Функциональный код Давида Тернера 1975 года с перебором делителей, который часто путают с решетом Эратосфена. Рассмотрим случай для .

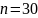Запишем натуральные числа, начиная от 2 до 30 в ряд:

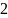3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

Первое простое число в списке 2. Вычеркнем из ряда все числа, кратные 2, начиная с .

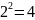3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

Следующее незачеркнутое простое число 3. Вычеркнем из ряда все числа, кратные 3, начиная с .

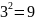3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

Следующее незачеркнутое простое число 5. Вычеркнем из ряда все числа, кратные 5, начиная с .

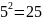3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

Были выполнены все зачеркивания чисел, кратных простому числу , для которых 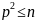. Незачёркнутыми оказались простые числа:

3 5 7 11 13 17 19 23 29

На практике важно не только получать список простых чисел, но и проверять, являются ли эти числа простыми. Алгоритмы, определяющие является ли число простым, называются тестами простоты.

Числа-близнецы

Два простых числа, которые отличаются на 2, как 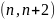получили образное название близнецы. В пределах первой сотни чисел расположены следующие пары близнецов: (3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61), (71, 73).

Все пары простых-близнецов, кроме (3, 5), имеют вид (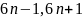 ). По модулю 30¹ все пары близнецов, кроме первых двух, имеют вид (11, 13), или (17, 19), или (29, 31).

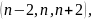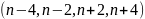В натуральном ряду чисел можно выделить тройку близнецов типа например (3,5,7) или четверку близнецов вида , например (5, 7, 11, 13) или (11, 13, 17, 19).

Тройки различных простых чисел, разность между наибольшим и наименьшим из которых равна шести, называются числами-триплетам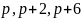и: ( ) или (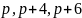 ). Примеры триплетов: (5, 7, 11), (7, 11, 13), (11, 13, 17), (13, 17, 19), (17, 19, 23).

Четверки простых чисел вида (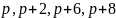 ) называют квадруплетами: (5, 7, 11, 13), (11, 13, 17, 19), (101, 103, 107, 109), (191, 193, 197, 199). По модулю 30 все квадруплеты, кроме первого, имеют вид (11, 13, 17, 19), а по модулю 210 имеют вид либо (101, 103, 107, 109), либо (191, 193, 197, 199).

Шестерки простых чисел вида (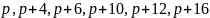 ) называют секступлетами: (7, 11, 13, 17, 19, 23), (97, 101, 103, 107, 109, 113). По модулю 210 все секступлеты, кроме первого, имеют вид (97, 101, 103, 107, 109, 113).

Работа с простыми числами важна не только для чистой математики. В криптографии большие простые числа используются в алгоритмах шифрования с открытым ключом.