
- •Множества. Основные понятия
- •Операции над множествами
- •Тождества теории множеств
- •Формулы включения-исключения
- •Множество n натуральных чисел
- •Множество z целых чисел
- •Множество q рациональных чисел
- •Множество j иррациональных чисел
- •Множество r действительных чисел
- •Задания для практических занятий
Основы теории множеств |
Занятие 1 |
Множества. Основные понятия
Понятие множества является основным,
неопределяемым понятием, поэтому можно
только пояснить этот термин. Под
множеством
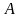 понимается собрание определенных и
различимых между собой объектов, мыслимое
как единое целое.
понимается собрание определенных и
различимых между собой объектов, мыслимое
как единое целое.
В этом интуитивном определении, принадлежащем немецкому математику Георгу Кантору (18451918), существенным является то обстоятельство, что собрание предметов само рассматривается как один предмет. Что касается самих предметов, которые входя во множество, то относительно них существует значительная свобода. Это может быть и множество целых чисел, и множество точек на плоскости и множество белых носорогов. Множество не обязательно должно содержать в каком-то смысле однородные объекты. Можно объединить в одном множестве и множество объектов и его одиночных представителей. Множества обычно обозначается заглавными латинскими буквами A, B, C,…. Множество можно задать списком, перечислив все его элементы:
При этом порядок, в котором элементы расположены при описании множества, не имеет значения. Не имеет значения также возможность неоднократного повторения одних и тех же элементов при описании множества. |
|
||
|
|||
Георг Фердинанд Людвиг Филипп Кантор |
К другому способу задания множества можно отнести порождающую процедуру, например,
|
(1.2) |
В данном случае под выражением
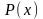 можно
понимать арифметические операции, или
некоторые неформальные описания.
можно
понимать арифметические операции, или
некоторые неформальные описания.
Пример. Множество
 содержит один элемент:
содержит один элемент:
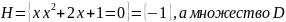 состоит из набора элементов
состоит из набора элементов
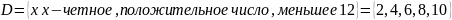 .
.
Определение множества, как совокупности всех неких объектов, которые обладают неким заданным нам свойством, не всегда может привести к однозначному ответу.
Пример Парадокс Рассела. Владелец парикмахерской в одном селе повесил следующее объявление: «Брею тех и только тех жителей села, кто не бреется сам». Спрашивается, кто бреет брадобрея?
Этот парадокс свидетельствует о том, что широко используемая теория множеств в ее интуитивном, «наивном» изложении является противоречивой. Формализация теории множеств, связанная, в частности, с устранением парадоксов, способствовала развитию не только методов теории множеств, но и такой науки, как математическая логика.
Символом
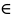 обозначается отношение принадлежности.
Запись
обозначается отношение принадлежности.
Запись
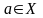 означает,
что элемент
означает,
что элемент
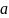 является элементом множества
является элементом множества
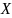 .
.
Определение 1.1. Множества
 и
и
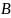 считаются равными, если они состоят из
одних и тех же элементов.
считаются равными, если они состоят из
одних и тех же элементов.
Записать утверждение о том, что множество равно множеству можно при помощи простой формулы
|
(1.3) |
Если множества состоят из разных элементов, то этот факт записывают
|
(1.4) |
Пример Даны три множества
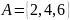 ,
,
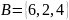 и
и
 .
В силу того, что все три множества состоят
из одних и тех же элементов, справедлива
запись
.
В силу того, что все три множества состоят
из одних и тех же элементов, справедлива
запись
 .
.
Пример 1.2.Даны два множества
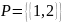 и
и
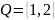 .
Эти множества нельзя считать равными,
так как единственным элементом множества
.
Эти множества нельзя считать равными,
так как единственным элементом множества
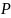 есть множество
есть множество
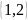 ,
множество
,
множество
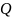 состоит из двух элементов: чисел 1 и 2.
состоит из двух элементов: чисел 1 и 2.
Определение 1.2. Если все элементы множества А принадлежат также множеству В, причем , то множество А является подмножеством В. Этот факт обозначают так:
|
(1.5) |
Определение 1.3. Если каждый элемент множества А есть элемент множества В, причем возможно , то множество В включает подмножеством А:
|
(1.6) |
Для наглядного представления отношений между подмножествами какого-либо универсального множества используются диаграммы Венна. Простые и лаконичные рисунки, которые впервые предложил английский математик Джон Венн (18341923), используются для иллюстрации взаимосвязей и в теории вероятности, и в логике, и в статистике и в информатике. В теории множеств
сами множества обозначают областями
и размещают внутри прямоугольника,
который представляет собой некое
универсальное множество |
|
Джон Венн |
Пример 1.5. Даны два множества
|
|
|
Множество, не содержащее элементов, называется пустым, и обозначается символом Ø. Пустое множество есть подмножество любого множества.
Множества бывают конечные и бесконечные. Конечные множества содержат конечное число элементов. Множества, не являющиеся конечными, называются бесконечными.
Число элементов конечного множества
называется его мощностью. Мощность
множества
обозначают
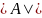 .
.
Пример 1.6. Дано множество
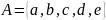 .
Тогда
=5.
.
Тогда
=5.
Множество всех подмножеств множества
называется множеством-степенью и
обозначается
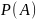 .
Если множество
состоит из
.
Если множество
состоит из
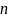 элементов, то множество
элементов, то множество
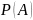 состоит из
состоит из
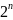 элементов.
элементов.
Пример 1.7. Дано множество
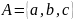 .
Множество-степень содержит следующие
подмножества:
.
Множество-степень содержит следующие
подмножества:
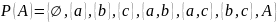

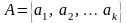

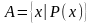
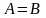
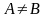
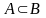
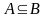
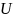 .
Если два множества имеют общие элементы,
то такие объекты иллюстрируются
перекрывающимися областями.
.
Если два множества имеют общие элементы,
то такие объекты иллюстрируются
перекрывающимися областями.
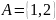 ,
и
,
и
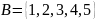 .
Для этих множеств справедливо
.
Для этих множеств справедливо
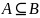 ,
поскольку множество
включает
множество
,
и каждый элемент множества
есть элемент множества
.
,
поскольку множество
включает
множество
,
и каждый элемент множества
есть элемент множества
.