Государственное образовательное учреждение

высшего профессионального образования

Пермский государственный технический университет

Учебное пособие

для выполнения практических и контрольных работ

по "Математике"

"Линейная алгебра”

Пермь 2010

"Линейная алгебра”. Методические указания для выполнения практических работ по курсу "Элементы высшей математики" для студентов всех специальностей.

Разработал: преподаватель А.С. Ремизова

Пояснительная записка

Методические указания представляют собой руководство к решению задач раздела "Линейная алгебра" курса "Элементы высшей математики" для студентов специальностей СПО на базе среднего (полного) общего образования.

Основное назначение пособия – помочь студенту самостоятельно, без помощи преподавателя изучить приемы решения основных задач, закрепить полученные навыки при выполнении практических работ и подготовиться к зачету по данному разделу.

§ 1. Определение матрицы. Действия над матрицами и векторами.

Матрицы

Виды матриц. Векторы

Равенство матриц

Линейные операции над матрицами

Умножение матриц

Свойства умножения матриц

1. Матрицы

Матрицей называется множество чисел, образующих прямоугольную таблицу, которая содержит m строк и n столбцов. Для записи матрицы используется следующее обозначение:

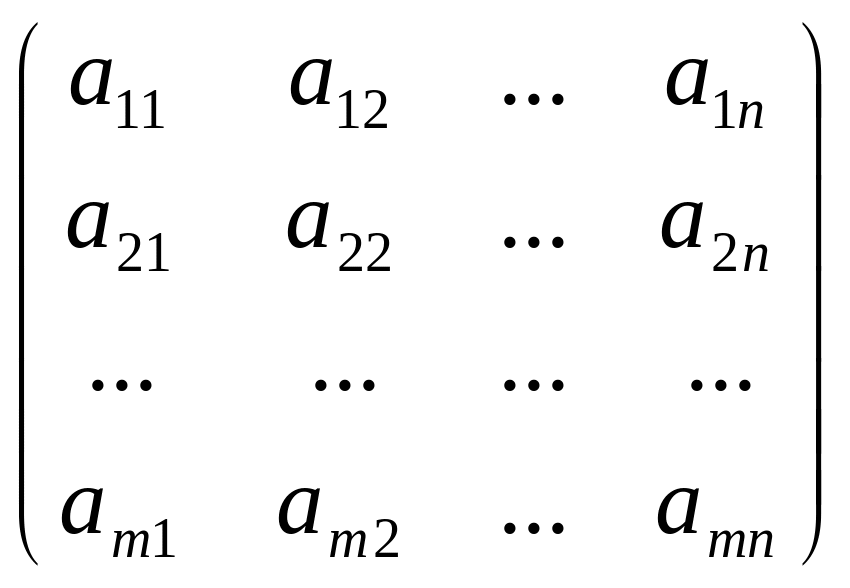
Для любого элемента a_ij первый индекс i означает номер строки, а второй индекс j – номер столбца. Сокращенно прямоугольную матрицу типа m×n можно записать так: А = (a_ij), где i = 1, 2, …, m; j = 1, 2, …, n.

2. Виды матриц. Векторы

Если число строк матрицы не равно числу столбцов (m ≠ n), то матрица называется прямоугольной. Таковы, например, матрицы

А = 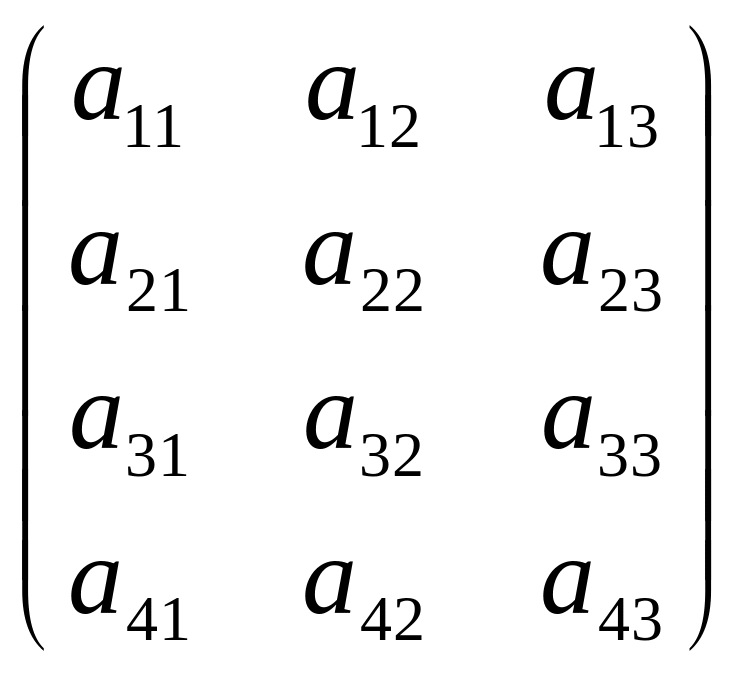, В = .

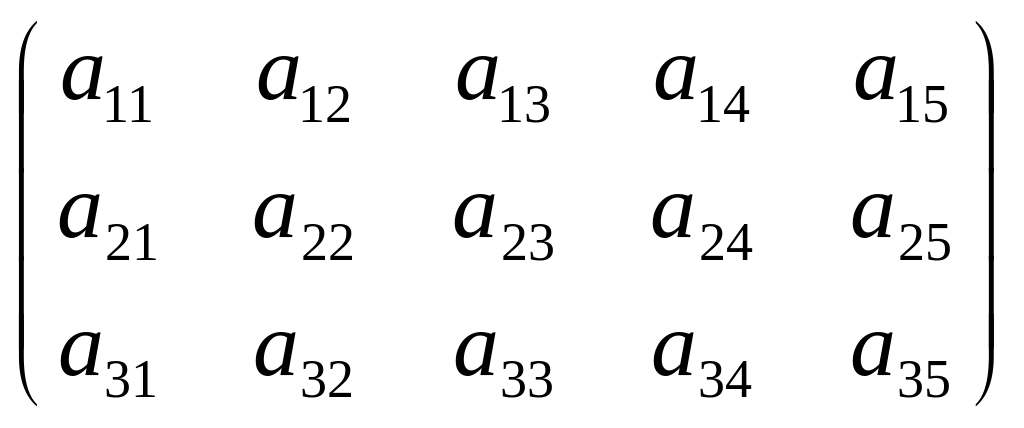Если число строк равно числу столбцов (m = n), то матрица называется квадратной. Например, квадратными являются матрицы

А = , В = .

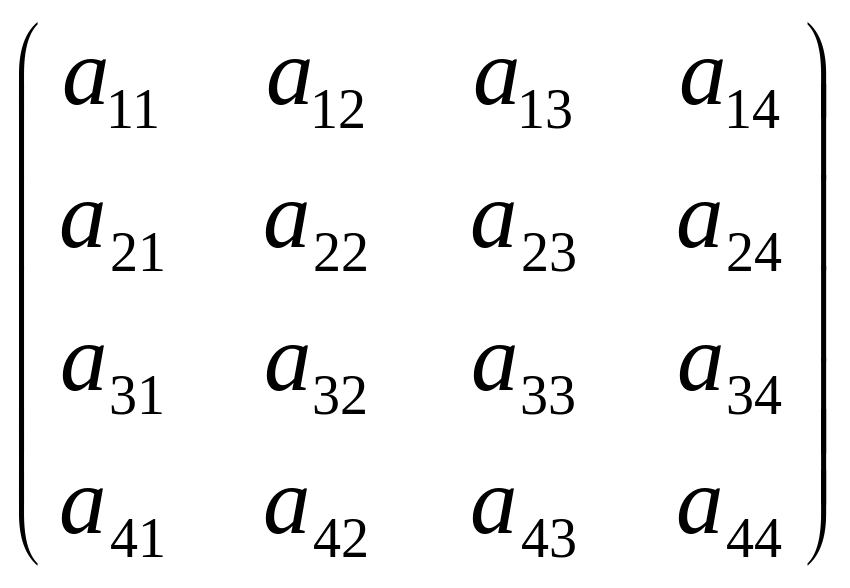Число строк или столбцов квадратной матрицы называется ее порядком. Так, в последнем примере порядок матрицы А равен 2, а порядок матрицы В равен 4.

Рассмотрим квадратную матрицу порядка п:

А = .

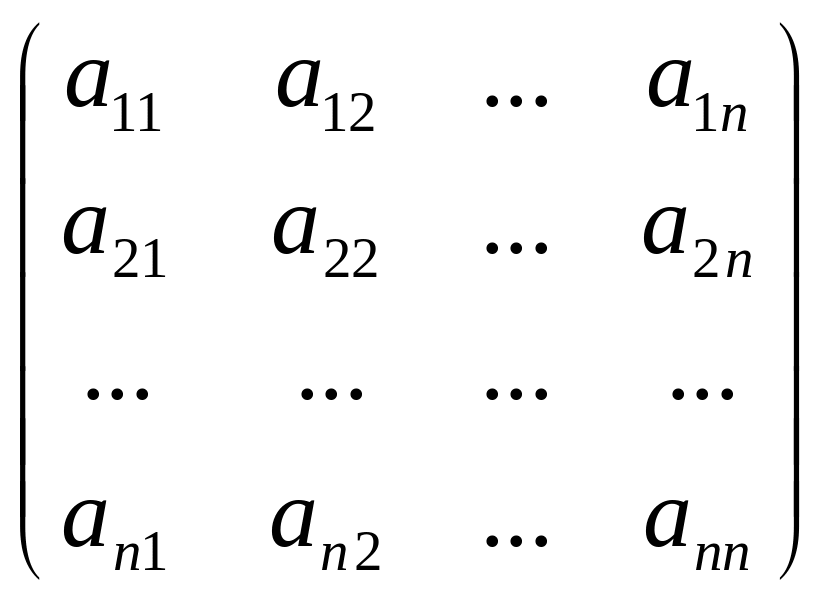Диагональ, содержащую элементы а₁₁, а₂₂, …, а_пп, будем называть главной, а диагональ, содержащую элементы а_1п, а_2,п-1, …, а_п1, - побочной (или вспомогательной).

Среди квадратных матриц выделим матрицы, у которых отличны от нуля только элементы, находящиеся на главной диагонали:

А = .

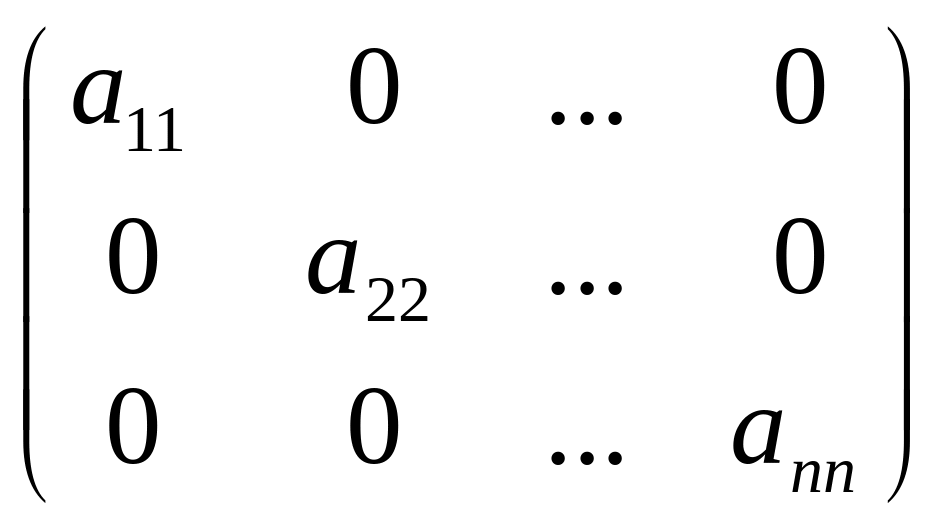Такие матрицы называются диагональными; например, матрицы

А = , В =

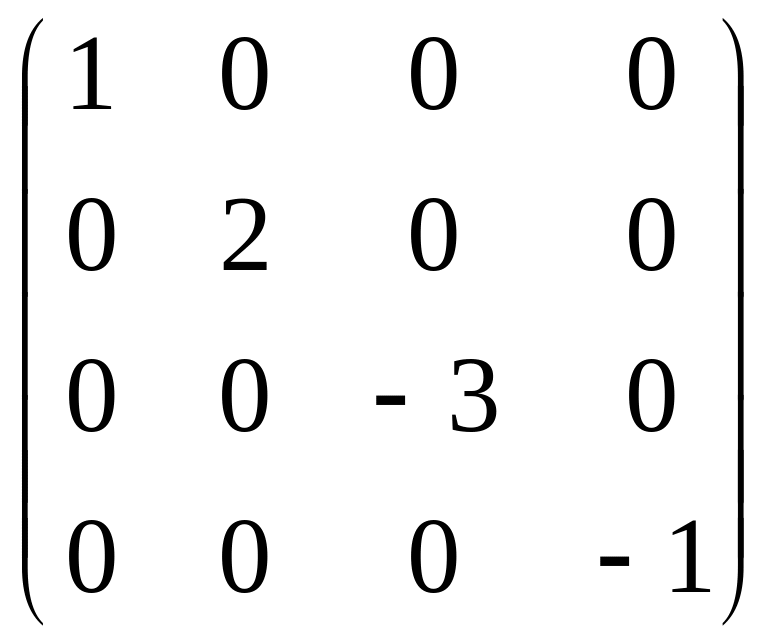
являются диагональными матрицами второго и четвертого порядка.

Если у диагональной матрицы все числа главной диагонали равны между собой, т.е. а₁₁ = а₂₂ = … = а_пп, то такая диагональная матрица называется скалярной. Если в скалярной матрице все числа главной диагонали равны единице, то матрица называется единичной и обозначается буквой Е:

Е = .

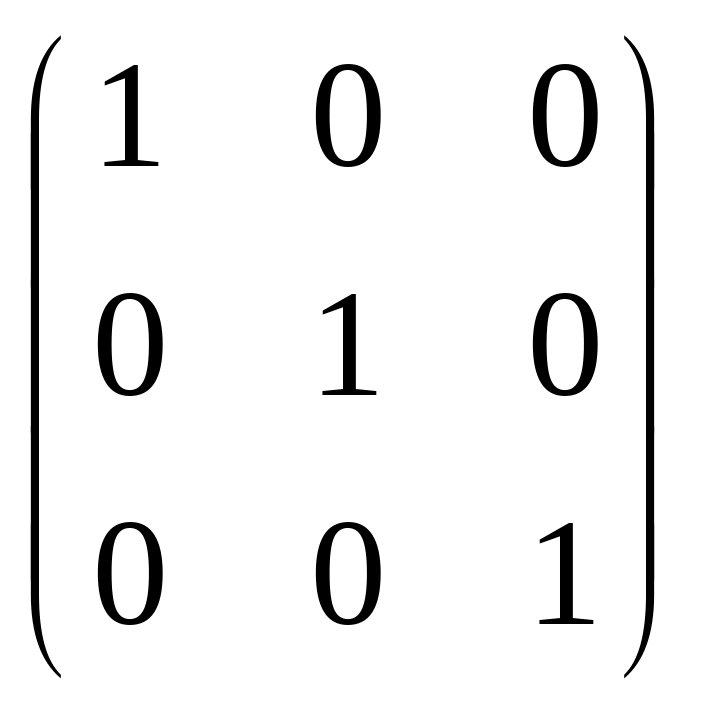Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается так:

О = .

В прямоугольной матрице типа т×п возможен случай, когда т = 1. При этом получается матрица-строка:

А = (а₁₁ а₁₂ … а_1п).

В случае, когда п = 1, получаем матрицу-столбец:

В = .

Такие матрицы- строки и матрицы-столбцы иначе будем называть векторами.

3. Равенство матриц

Две матрицы называются равными, если они имеют одинаковое число строк т и одинаковое число столбцов п и их соответствующие элементы равны: a_ij = b_ij.

Так, матрицы А = и В = равны, если a₁₁ = b₁₁, a₁₂ = b₁₂, a₁₃ = b₁₃, a₂₁ = b₂₁, a₂₂ = b_22, a₂₃ = b₂₃.

Равные матрицы обязательно имеют одно и то же строение: либо обе они прямоугольные типа т×п , либо квадратные одного и того же порядка п.

Если в матрице типа т×п, имеющей вид

А =

переставить строки со столбцами, получим матрицу типа п×т, которую будем называть транспонированной матрицей:

А^Т = .

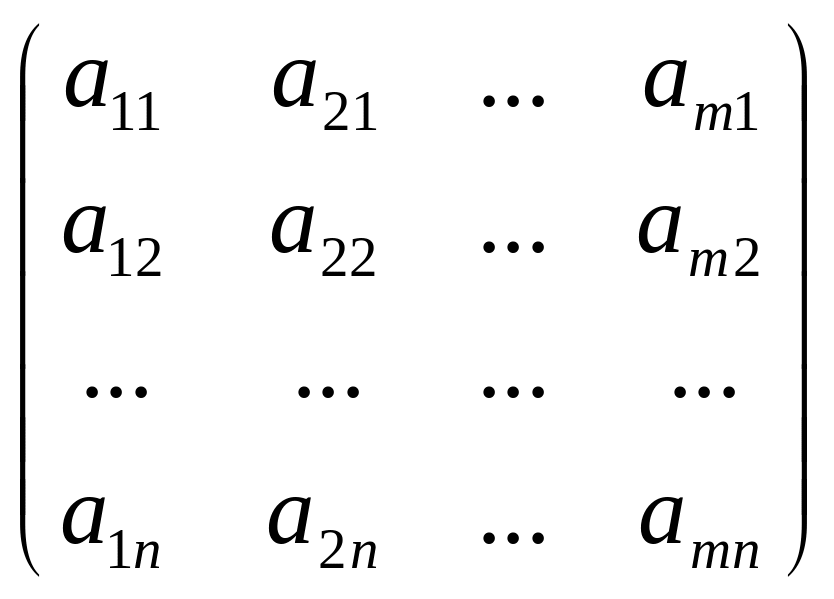В том случае, когда матрица состоит из одной строки (матрица-строка), т.е.

В = (b₁ b₂ … b_n),

транспонированная матрица является матрицей-столбцом:

В^Т = .