2. Нормальное распределение

Нормальным (гауссовским) называют распределение непрерывной с. в., с плотностью вероятности вида

. (П.1.3)

Из этого выражения следует, что нормальное распределение определяется двумя параметрами: a (математическим ожиданием) и σ² (дисперсией). Принадлежность с. в. Х к нормальному распределению с параметрами a и σ² обозначается Х ~ N(a, σ²).

Функция распределения нормального закона:

. (П.1.4)

Математическое ожидание и дисперсия нормально распределенной непрерывной с. в.:

.

.

Замечательным свойством нормального распределения служит возможность выражения центральных моментов высших порядков через дисперсию. Это объясняет, почему во многих приложениях (при анализе и синтезе СС, решении задач оценки и проч.) широко используются первые два момента нормального распределения.

Так, для центральных моментов μ_k k-го порядка нормально распределенной с. в. справедливо следующее рекуррентное соотношение:

μ_k = (k – 1)² μ_{k – 2}; k ≥ 2, 3, 4, …; μ₂ = σ², μ₄ = 3σ⁴, μ₆ = 15σ⁶

и т. д.

Из этого следует, что центральные моменты нечетных порядков равны нулю, т. е. μ₁ = μ₃ = μ₅ = … = 0.

В среде Mathcad нормальному закону распределения соответствуют встроенные функции, с корневым словом norm и первым символом d, p, q, r:

dnorm (x, a, ) — выводит значения плотности f(x) ((П.1.3));

pnorm (x, a, ) — выводит значения F(x) (П.1.4);

qnorm (A, a, ) — выводит значение квантили порядка A;

rnorm (n, a, ) — выводит массив (вектор-столбец) из n значений нормально распределенных независимых случайных чисел с математическим ожиданием a и стандартом отклонения .

Формы кривых плотности и функции нормального распределения приведены на рис. П.1.2. Плотность f1(x) и функция распределения F(x) построены для а = 2,  = 1. Плотность f2(x) построена для а = 2,  = 0,5. Сопоставляя кривые f1(x) и f2(x), можно заметить, что значение  влияет на форму плотности нормального распределения: при увеличении  кривая f(x) (П.1.3) становится более пологой, а ее максимальное значение, равное , снижается. При уменьшении  кривая f(x) более компактно располагается вокруг центра распределения и приобретает более вытянутую острую вершину. Изменение значения а не влияет на форму кривой f(x), поскольку при таком изменении меняется лишь положение оси симметрии f(x).

Нормальное распределение относится к симметричным распределениям с центром распределения (математическим ожиданием), равным a.

Вероятности того, что нормально распределенная с. в. отклоняется от своего математического ожидания m не более чем на , 2, 3, 4, определяются в следующем фрагменте файла Mathcad (см. рис. П.1.3).

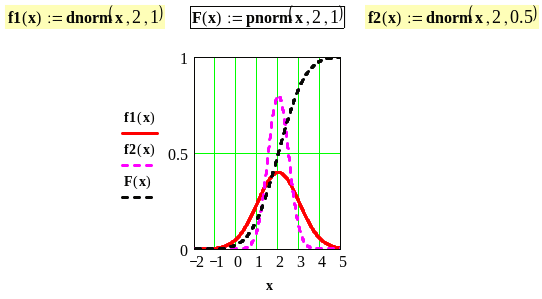
Рис. П.1.2. Вид плотностей и функции нормального распределения

Рис. П.1.3. Вычисления вероятностей отклонений

Вероятность отклонения нормально распределенной с. в. Х на  3 от своего математического ожидания равна 0,9973 (правило 3-х сигм).