8.5. Критерии принятия решений

При анализе наиболее выгодной стратегии в условиях неопределенности может использоваться несколько критериев. Среди них:

‑ критерий гарантированного результата;

‑ оптимистический критерий;

‑ пессимистический критерий;

‑ критерий наименьшего вреда (Сэвиджа);

‑ критерий обобщенного максимина (Гурвица).

В зависимости от специфики задачи принятия решений, каждый из перечисленных критериев имеет свои особенности, достоинства и недостатки, которые необходимо учитывать. В ряде задач принятия решений, перечисленные критерии могут использоваться в совокупности. Рассмотрим вкратце сущность этих критериев.

Критерий гарантированного результата. Этот критерий носит также название максиминного критерия Вальда. Он позволяет принять решение, обеспечивающее лучший из наихудших результатов.

Предположим, что построена платежная матрица вида:

Сj Si	C1	C2	…	Сk	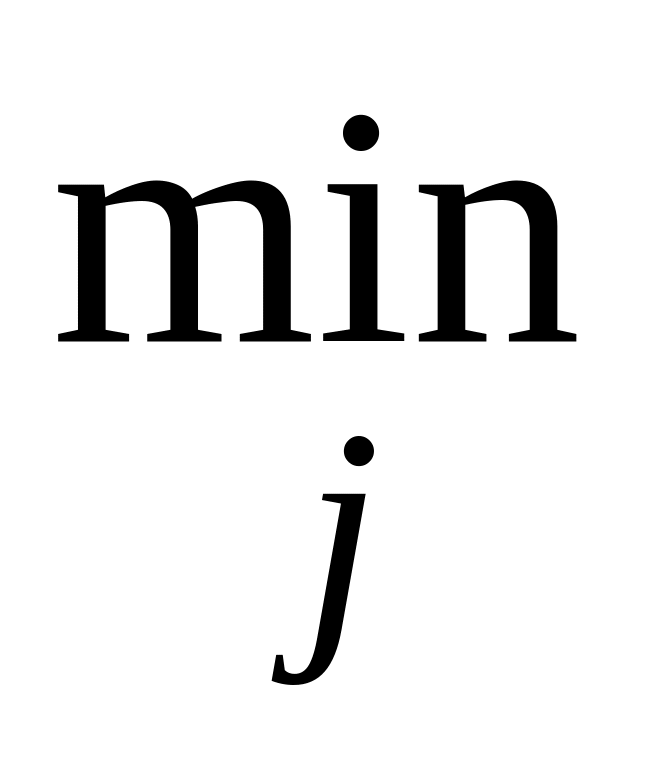(еij)
S1	е11	е12	…	е1k	e1min
S2	е21	е22	…	е2k	e2min
…	…	…	…	…	…
Sm	еm1	еm2	…	еmk	em min

В этой матрице S_i — множество стратегий (вариантов решений, альтернатив) игрока 1; С_j — совокупность факторов, в условиях которых игрок 1 принимает решения. Стратегии S_i могут быть названы контролируемыми, управляемыми факторами (например, варианты структур технических систем, алгоритмов управления ими, инвестиций в экономике и проч.). Факторы С_j, не поддающиеся контролю (например, уровень внешних воздействий на техническую систему, индексы цен в экономическом пространстве). Каждой паре контролируемых и неконтролируемых факторов ставится в соответствие мера эффективности Е(S_i, C_j) = е_ij. На основе платежной матрицы, игрок 1 определяет минимально возможные выигрыши e_{i min} для каждой из своих стратегий. В результате он получает вектор минимальных выигрышей Е_min = | e_1min e_2min . . . e_{m min} |^Т, который используется для выбора той стратегии S_Г, которая соответствует максимальному элементу вектора Е_min. Таким образом, критерий гарантированного результата (критерий Вальда) может быть записан в форме:

S_Г: (Е_min) = (е_ij). (8.38)

Данный критерий обеспечивает выбор стратегии, соответствующей максимизации минимального выигрыша или, что то же самое, минимизации максимальных ущербов, потерь, которые могут иметь место при реализации игроком 1 своих стратегий. Использование такого критерия оправдано, если игрок 1 не заинтересован в крупном выигрыше, но хочет застраховать себя от неожиданных проигрышей. Понятно, что выбор такого критерия, рассчитанного на наилучший из худших вариантов, определяется отношением игрока 1 к риску. Принятие решений по критерию (8.38) позволяет минимизировать риск, но не дает возможности достичь существенного выигрыша.

В ряде экономических задач критерий (8.38) может быть записан в затратной форме:

S_Г: (З_max) = (З_ij). (8.39)

Здесь З_ij ‑ элемент матрицы затрат.

Критерий оптимизма. Этот критерий носит название критерия максимакса и соответствует оптимистической наступательной стратегии. При выборе этого критерия не принимается во внимание никакой возможный вариант, кроме наилучшего. Однако следует учесть, что критерий оптимизма принесет реальный выигрыш только в том случае, когда внешние условия реализации проекта будут для него благоприятными. Поэтому рациональная область применения данного критерия ограничивается случаями, в которых игрок 1 имеет возможность повлиять на стратегии другой стороны. В других случаях появляется риск не достичь желаемого результата.

Критерию оптимизма соответствует наибольшее значение выигрыша в платежной матрице:

S_maxmax: (Е_max) = (е_ij); Е_max = | e_1maxe_2max . . . e_{m max} |^Т. (8.40)

Если вместо платежной матрицы рассматривается матрица затрат, то критерий оптимизма может быть записан в виде:

S_maxmax: (З_min) = (З_ij). (8.41)

Отметим здесь, что ситуации, требующие применения критерия максимакса, в общем случае нередки. Этим критерием пользуются не только безоглядные оптимисты, но и игроки, поставленные в безвыходное положение, когда они вынуждены пользоваться принципом «или пан, или пропал».

Критерий пессимизма. Этот критерий — полная противоположность предыдущему. Критерий пессимизма предполагает использование управляемых факторов неблагоприятным образом, так, что

S_minmin: (Е_min) = (е_ij). (8.42)

S_minmin: (З_max) = (З_ij). (8.43)

При кажущейся нерациональности применения критерия (8.43), необходимость его практического использования часто вызывается невозможностью в полной мере управлять располагаемым набором стратегий S_i ввиду наличия неопределенности. Чаще всего такая неопределенность связана с фактором времени, необходимостью прогнозировать развитие каких-либо ситуаций. Например, издержки производства на коротких временных интервалах являются достаточно определенными (контролируемыми). Однако при анализе длительных процессов, которые составляют несколько лет, некоторые элементы указанных издержек становятся неопределенными (неконтролируемыми). К таким элементам можно отнести, например, стоимость материалов, электроэнергии и проч.

Критерий наименьшего вреда (Сэвиджа). При использовании рассмотренных выше критериев возможны ситуации, когда неконтролируемые факторы будут действовать более благоприятным образом по сравнению с наихудшим состоянием, на которое ориентировался игрок 1. Такими факторами могут служить условия, более благоприятные по сравнению с прогнозируемыми (метеоусловия, цены, состояние оборудования и проч.). В подобных ситуациях полезный эффект может значительно отличаться от результата, который обеспечивался бы при использовании критерия гарантированного результата или критерия пессимизма. Возникает проблема оценки возможных отклонений получаемых результатов от их оптимальных значений. Решение этой проблемы находят, используя матрицы рисков (8.37).

Критерий наименьшего вреда позволяет определить худшие возможные последствия для каждой альтернативы и выбрать альтернативу с лучшим из худших результатов. По этой причине данный критерий носит название критерия минимаксного риска. Принятие решения на его основе формально аналогично выбору стратегии по критерию Вальда (8.38) с тем отличием, что игрок 1 руководствуется не платежной матрицей, а матрицей рисков с элементами r_ij (8.37).

Критерию Сэвиджа соответствует следующая формульная запись:

S_R: (R_max) = (r_ij). (8.44)

Принятие решения по этому критерию позволяет обеспечить минимальный риск в самой неблагоприятной ситуации.

Критерий обобщенного максимина (Гурвица). Этот критерий позволяет принимать решение, руководствуясь промежуточным состоянием между крайним пессимизмом и безудержным оптимизмом. В соответствии с этим компромиссом данный критерий представляет собой следующую линейную комбинацию:

S_G: [ (e_ij) + (1 – ) (e_ij)]. (8.45)

Нетрудно видеть, что при 0критерий Гурвица совпадает с критерием оптимизма (8.40), т. е. ориентирует ситуацию на получение наибольшего выигрыша и неизбежно сопровождающий это решение предельный риск. При  критерий (8.45) соответствует критерию гарантированного результата Вальда (8.38). Значения между 0 и 1 являются промежуточными между большим риском и осторожностью, позволяя лицу, принимающему решение выразить свое отношение к риску.

При выборе варианта принятия решения обычно не рекомендуется останавливаться на использовании какого-то одного критерия из рассмотренной совокупности критериев. Этот совет позволит избежать неоправданных решений и экономических потерь. В практике решения задач, связанных с принятием решений, рассмотренные критерии применяются в совокупности. Например, наряду с критерием гарантированного результата может быть использован критерий Сэвиджа, критерий минимаксного риска может дополняться критерием пессимизма и другими.

Практика показывает, что комплексное использование различных критериев эффективности решений может стать определяющим. Например, получила распространение следующая схема принятия решений с использованием критериев (8.38)-(8.45):

‑ составляются матрицы выигрышей, затрат и рисков;

‑ выбираются стратегии, наиболее эффективные с точки зрения критериев (8.38)-(8.45);

‑ к практическому применению рекомендуется та стратегия из числа выбранных, которая удовлетворяет наибольшему числу критериев.

Подобная процедура принятия решения базируется на упрощенном предположении о том, что степень надежности выбираемой стратегии связан с числом критериев, которым она удовлетворяет. Несмотря на простоту решающего правила, подобная процедура может считаться приемлемой для достаточно широкого круга практических задач. В общем случае элементы рассмотренных фыше матриц являются случайными. Их числовые харктеристики, вид распределений может быть определен в процессе статистического моделирования, получения результатов компьютерных экспериментов над ИМ исследуемых систем. При этом критерии (8.38)-(8.45) формируются с использованием математических ожиданий (или их оценок по экспериментальным данным).