8.1.2. Линейная регрессия. Метод наименьших квадратов

Пусть по данным наблюдений получены вектор Y значений откликов y_i и вектор Х значений фактора х_i, i = . Используя эти данные, требуется построить, линейную регрессию:

у_i = ₀ + ₁ х_i + ₂ (х_i)² + ... + ε_i, i = , (8.6)

где ₀, ₁ — неизвестные параметры, подлежащие определению; ε₁, ε₂, …, ε_n — независимые нормально распределенные случайные величины с нулевым математическим ожиданием и дисперсией, т. е. ε_i ~ N(0, ²).

Значения ε_i могут быть вызваны совокупным влиянием множества независимых случайных воздействий, таких как инструментальные погрешности приборов наблюдений, методические погрешности процессов измерений, случайным разбросом условий проведения испытаний и проч. Это совокупное влияние разнообразных причин служит обоснованием предположения о нормальном распределении величин ε_i в силу центральной предельной теоремы.

Представим n уравнений (8.6) в векторно-матричной форме:

Y = А + ε, Y = (у₁, у₂, …, у_n)^Т, (8.7)

ε = (ε₁, ε₂, …, ε_n)^Т, R = cov(ε) = ²Е_n.

Здесь  ‑ вектор неизвестных параметров, для случая простой линейной регрессии имеющий вид  = (₀, ₁)^Т; R — (n  n)-ковариационная матрица вектора ε; Е_n ‑ единичная матрица порядка n. Заметим, что выражение (8.7) служит общей формой для задач линейной регрессии, конкретный вариант которых определяется размерностью вектора  и структурой матрицы А. Для варианта простой линейной регрессии (8.6) вектор  имеет два элемента, а (n  2)-матрица А имеет два столбца, первый из которых содержит n единиц, а второй — элементы вектора Х:

А = [1 | X] = ;  = | ₀, ₁ |^Т. (8.8)

Задача линейной регрессии состоит в получении вектора оценок неизвестных параметров. Для ее решения необходимо ввести критерий близости элементов вектора Y и вектора регрессионных зависимостей А. Этот критерий обычно формируется в виде суммы квадратов отклонений элементов вектора Y от А, т. е. в виде суммы квадратов элементов вектора ε (квадратов невязок). Например, в задаче простой линейной регрессии критерий записывается в виде суммы квадратов отклонений элементов вектора Y от прямой линии с параметрами (₀, ₁):

G() = = . (8.9)

Для определения параметров линейной регрессии следует найти минимум критерия подобного вида. Минимизация критериев вида (8.9) составляет сущность метода наименьших квадратов (МНК). Этот метод позволяет получить решение в двух видах — в форме обобщенного обращения неквадратной матрицы А и в рекуррентной форме. Последняя форма удобна в практических приложениях для получения текущих оценок параметров  в процессе последовательных экспериментов. Она рассмотрена в [3].

Известно, что решение задачи линейной регрессии (8.7) по критерию (8.9), в предположении неособенности матрицы А^ТА имеет вид

= (А^ТА)^{– 1} А^ТY (8.10)

Качество оценок (8.10) характеризует вектор е ошибок оценок

е = – . (8.11)

Матрица А^# = (А^ТА)^{– 1}А^Т носит название обобщенной обратной матрицы, поэтому выражение (8.10) называют решением задачи оценки методом наименьших квадратов (или алгоритмом МНК) в форме обобщенного обращения.

Получение оценок (8.10) позволяет, в свою очередь, получить оценки откликов, выражения для которых следуют из (8.7):

= А . (8.12)

Ошибки оценки откликов характеризуются выражением

е_у = – Y, (8.13)

где е_у — вектор ошибок оценок откликов, элементы которого содержат значения остаточных (после решения задачи регрессии) невязок. Сумма квадратов элементов вектора е_у (8.13) называется остаточной суммой квадратов S = . Значение S характеризует точность решения задачи регрессии.

С использованием (5.17) могут быть получены соотношения для оценок откликов в конкретных задачах линейной регрессии. Так, в случае простой линейной регрессии из (8.12), для i-го значения фактора имеем:

= + х_i ; i= . (8.14)

Подобные выражения остаются справедливыми для произвольных значений факторов, в том числе — для х_j при j > n, т. е. соотношения типа (8.14) могут быть использованы и для прогноза (экстраполяции) значений откликов после завершения экспериментов.

Полученные МНК-оценки линейной регрессии обладают рядом важных с практической точки зрения свойств:

1. Оценки (8.10) параметров линейной регрессии (8.7) доставляют минимум критерию (8.9), являются несмещенными и эффективными.

2. Ковариационная (m  m)-матрица Р ошибок оценок (8.11) равна

Р = cov(е) = cov( ) = ²(А^ТА)^{– 1}. (8.15)

3. Ковариационная (n  n)-матрица оценок откликов (8.12)

= cov( ) = АРА^Т = ²A(А^ТА)^{– 1} А^Т

4. Ковариационная (n  n)-матрица ошибок оценки откликов (8.13)

Р_у = cov(е_у) = ²[Е_n – A(А^ТА)^{– 1} А^Т] = ² Е_n – .

5. Дисперсии оценок параметров расположены на диагонали матрицы Р (8.15), а дисперсии откликов размещаются на диагонали матрицы .

6. Оценки (8.10), (8.12) нормально распределены с математическими ожиданиями , А и ковариационными матрицами Р (8.15) и соответственно.

Полученные выше общие соотношения справедливы для произвольных задач линейной регрессии (простой, квадратичной, множественной и др.). Эти соотношения удобно использовать для анализа конкретных задач этого класса с применением СКМ и получения как численных, так и аналитических результатов. Однако формулы типа (8.15) содержат дисперсию невязок ², которая при решении задач регрессии неизвестна. Это затрудняет статистический анализ результатов решения. Для выполнения такого статистического анализа требуется вычислить оценку дисперсии невязок ² по исходным данным задачи регрессии. Такой оценкой служит остаточная дисперсия, значение которой по выборочным данным находят в виде:

= ( – Y) ^Т ( – Y) / n = (е_у)^Те_у / n = S / n, (8.16)

где = А — вектор оценок откликов (8.12); S — остаточная сумма квадратов; n — число экспериментов.

На рис. 8.1 приведено решение типовой задачи линейной регрессии. В качестве регрессионного соотношения принят полином второго порядка.

Матрица А формируется (см. рис. 8.1) в виде совокупности столбцов, объединенных встроенной функцией augment. В mcd-файле обозначены: Y — вектор откликов;  — вектор оценок параметров; Y₀ — вектор оценок откликов (8.12); Δ — вектор ошибок оценки откликов е_у; δ — остаточная сумма квадратов S; d — остаточная дисперсия (8.16); E — единичная матрица порядка n; Р, Р0, Р1 — ковариационные матрицы оценок параметров (8.15), оценок откликов и ошибок оценок откликов соответственно. На графике изображены: исходные значения элементов вектора откликов Y_i (i = 0, 1, ..., 9) и оценки откликов Y_0i = –0,753 – 0,078 х_i + 0,178 (х_i)². Результаты анализа качества полученных оценок свидетельствуют о незначительных погрешностях этого варианта регрессии. Так, остаточная сумма квадратов, равна 0,91, остаточная дисперсия, равна 0,091. Эти показатели качества могут использоваться для сопоставительного анализа вариантов регрессионных соотношений в задачах регрессии.

Рис. 8.1. Решение задачи линейной регрессии

Множественная регрессия. Анализ задач линейной регрессии, проведенный выше, опирался на варианты, в которых имелся один фактор. В практике статистического моделирования распространены также задачи, в которых требуется выявить зависимость некоторой случайной величины от нескольких случайных (или неслучайных) величин. Такие задачи составляют класс задач множественной регрессии.

В задачах множественной линейной регрессии выражения f(X_i, ) в (8.1) имеют линейный относительно неизвестных параметров  вид:

у = ₀ + ₁ х₁ + ₂ х₂ + ε;

у = ₀ + ₁ х₁ + ₂(х₂)² + ε;

у = ₀ + ₁sin(х₁) + ₂sin(х₂) + ε.

Как и ранее, каждая из приведенных зависимостей составляет структуру i-го уравнения в системе линейных алгебраических уравнений (8.7), например,

y_i = ₀ + ₁х_1i + ₂(х_2i)² + ε_i, i = , (8.17)

где y_i ‑ отклик в i-ом эксперименте; х_1i и х_2i ‑ значения первого и второго факторов в i-ом эксперименте; ₀, ₁, ₂ ‑ искомые параметры, составляющие вектор ; ε_i ‑ i-ая невязка, совокупность которых входит в вектор ε. Регрессионная зависимость в уравнении типа (8.17) может быть представлена в форме произведения строки [1 х_1i (х_2i)²] на вектор параметров . Совокупность строк аналогичного вида, записанных для каждого из испытаний, составляет (n  m)-матрицу А, где m ‑ число искомых параметров.

Предполагая, как и ранее, что невязки ε_i ‑ независимые случайные нормально распределенные случайные величины с нулевым математическим ожиданием M(ε_i) = 0 и дисперсией D(ε_i) = ², модель множественной регрессии может быть представлена в форме системы n линейных алгебраических уравнений вида

Y = А + ε, Y = (у₁, у₂, …, у_n)^Т, ε = (ε₁, ε₂, …, ε_n)^Т, R = cov(ε) = ²Е_n.

Эта модель полностью аналогична выражениям (8.7),которые были рассмотрены выше. Поэтому, алгоритм (8.10) решения задачи линейной регрессии и свойства получаемых оценок полностью применимы и к задачам множественной линейной регрессии.

Рекуррентный алгоритм МНК. Рассмотренные алгоритмы решения задач линейной регрессии вида (8.10) обеспечивают возможность оценки параметров регрессионных соотношений только после завершения серии компьютерных экспериментов (или наблюдений, измерений в натурных экспериментах). В практике статистического моделирования, исследования систем различных классов весьма часто встречаются итеративные процедуры и так называемые рекуррентные соотношения, которые позволяют последовательно получать очередной результат с использованием предыдущего. Распространенность рекуррентных алгоритмов обработки данных определяется простотой их программирования, отсутствием необходимости запоминания больших объемов данных, а также возможностью получения и использования промежуточных оценок в реальном времени.

Классическим примером служит, например, последовательное наблюдение (измерение) траектории летательного аппарата с целью оперативной оценки параметров его движения по информации, имеющейся в наличии на момент вычисления оценок. Эти промежуточные оценки позволяют, например, использовать их для коррекции траектории объекта в случае выявленных ее отклонений. Традиционные алгоритмы типа (8.10) позволяют получать оценки лишь после завершения процесса измерений и накопления всех данных, т. е. после завершения эксперимента. Это исключает возможность использования результата для оперативного вмешательства в наблюдаемые процессы.

Рекуррентные алгоритмы обеспечивают такую возможность, поскольку основаны на пересчете предыдущей оценки вектора параметров путем использования очередного измерения. При такой процедуре нет необходимости в накоплении и хранении всей предыстории, а полученные текущие оценки могут быть использованы для принятия оперативного решения в режиме реального времени.

Преимущества рекуррентных процедур видны уже при рассмотрении, например, алгоритма вычисления выборочного среднего для некоторого массива данных х_i, (i = ). Следуя первому из упомянутых выше принципов обработки данных, среднее значение может быть получено с использованием формулы , т. е. для определения необходимо предварительно накопить все значения х_i. Однако может быть получено последовательным рекуррентным использованием каждого следующего элемента массива данных: , где у_i ‑ среднее по первым i значениям. Подобный принцип вычисления оценок может быть применен и для решения задач линейной регрессии.

Для реализации этого принципа будем рассматривать результаты измерений в виде последовательного ряда чисел y_i (i = ), получаемых на i-ом такте измерений. Учитывая, что оценке подлежат константы (не зависящие от номера такта), запишем регрессионные зависимости вида (8.3)-(8.5), (8.17) в форме разностных уравнений:

_i = _{i – 1} ; y_i = a_i _i + ε_i; ₀ = М(₀). (8.18)

Здесь: _i, y_i — вектор параметров и значение отклика на i-ом такте измерений; a_i — i-ая строка матрицы А системы алгебраических уравнений (8.7); ε_i — i-ый элемент вектора невязок ε = (ε₁, ε₂, …, ε_n)^Т.

Существует несколько путей формирования рекуррентной процедуры оценивания параметров линейной регрессии [3]. Опуская вывод, приведем окончательный вид рекуррентного алгоритма оценивания:

= + Si – 1 (ai Si – 1 + 1) – 1 (yi – ai ); Si = Si – 1 – Si – 1 (ai Si – 1 + 1) – 1 ai Si – 1.

(8.19)

Начальное значение матрицы S, необходимое для рекуррентной процедуры (8.19), можно выбрать с использованием первых m уравнений системы (8.7), где m — число искомых параметров регрессии.

Сопоставление результатов, получаемых с применением алгоритмов (8.10) и (8.19) показывает полную идентичность получаемых оценок. В подтверждение этого положения применим рекуррентный алгоритм (8.19) для обработки данных, использованных на рис. 8.1. Результат применения процедуры (8.19) приведем на рис. 8.2.

Процедура получения начальных условий для алгоритма (8.19) приведена на рис. 8.2, а. Задается i-ая строка матрицы А (в первой строке рис. 8.2, а), с применением функции stack формируется матрицу А₃, содержащую первые 3 строки матрицы А (см. рис. 8.1). Аналогично, с помощью функции stack формируется вектор Y₃, содержащий первые три элемента вектора данных Y. Далее определяются необходимые начальные данные, которые в файле (см. рис. 8.2, а) обозначены ₃ и s₃.

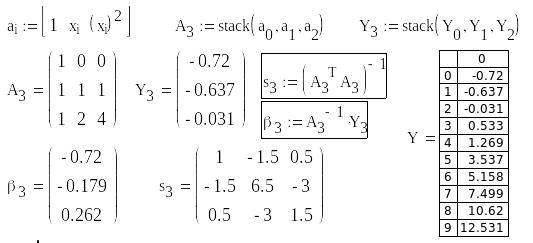
Рис. 8.2, а. Определение начальных условий

Последующие вычисления по алгоритму (8.19) используют циклическую процедуру, один из вариантов которой приведен на рис. 8.2, б. Простота этого цикла исключает необходимость подробных пояснений. В матрице справа приведены последовательные значения получаемых оценок параметров, конечные значения которых совпадают с результатом решения этой задачи традиционным алгоритмом МНК (см. рис. 8.1).

Рис. 8.2, б. Последовательное вычисление оценок