7.2. Статистическое распределение выборки

При рассмотрении дискретных случайных величин (см. п. 5.1.1) отмечалось, что их распределение задается совокупностью возможных значений и вероятностей каждого из этих значений. Применительно к выборочным данным используется близкий по смыслу подход на основе так называемого статистического распределения, под которым понимается совокупность элементов выборки и соответствующих им частот.

Рассмотрим выборку объемом n, причем в процессе формирования выборки элемент y₁ наблюдался n₁ раз, y₂ — n₂ раз, … y_k — n_k раз ( = n).

Статистическое распределение выборки в данном случае соответствует совокупности отобранных (измеренных) значений y_j и соответствующих им частот n_j, j = 1, 2, …, k. В статистических распределениях используются также и относительные частоты n_j / n.

Упорядоченные статистические данные порождают понятия вариационного и статистического ряда.

Вариационным рядом называют совокупность всех элементов выборки, записанных в неубывающем порядке. Поэтому в вариационном ряде могут присутствовать одинаковые элементы (если они имеют место в выборочных данных), а максимальный и минимальный элементы служат крайними элементами вариационного ряда, т. е. , . Разность R = крайних значений вариационного ряда определяет размах (ширину) выборки, а отдельные элементы вариационного ряда носят название порядковых статистик.

Статистическим рядом называют последовательность различных элементов выборки y₁, y₂, …, y_m , записанных в возрастающем порядке, и частот n₁, n₂, …, n_m , с которыми эти элементы содержатся в выборке.

Удобной формой служит табличная форма представления статистического ряда:

y1 y2 … ym n1 n2 … nm

.

При решении прикладных статистических задач часто используется также статистический ряд, составленный для относительных частот w_i = n_i / n:

y1 y2 … ym w1 w2 … wm

.

Графически статистический ряд представляется в виде полигона частот, по оси абсцисс которого откладываются элементы y_i, а по ординатам — абсолютные или относительные частоты; точки полученного графика соединяют отрезками прямых.

В практике статистического моделирования достаточно часто встречаются выборки значительных объемов. Решение ряда задач в этих условиях может потребовать «сжатия» полученных данных, что обеспечивается использованием так называемого группированного статистического ряда. Этот ряд служит основой построения гистограмм. Он образуется путем разделения диапазона [х_min, х_max] выборочных данных на b промежутков х_k (k = 0, 1, …. b – 1) и определения чисел n_k попаданий выборочных данных в каждый промежуток. Исходная выборка при этом заменяется значениями середин промежутков и частот n_k.

Поскольку группированный статистический ряд используется для построения гистограмм, он полезен при предварительном анализе вида распределения случайных величин по выборочным данным. Но преобразование исходной выборки в группированный статистический ряд неизбежно влечет появление дополнительных (в данном случае — методических) погрешностей в исходных данных. Однако уровень таких погрешностей обычно не является значительным.

Пример 7.1. Проведено n = 10 измерений отклонения напряжения сети от номинального уровня. Полученные данные, с точностью до вольта, составили следующую выборку:

Х = [0, – 1, – 3, 2, 1, 0, – 1, – 2, 1, – 1] ^Т.

Сформировать вариационный, статистический и группированный ряды.

Решение. Вариационным рядом для этой выборки служит последовательность значений: – 3, – 2, – 1, – 1, – 1, 0, 0, 1, 1, 2, причем х_min = – 3; х_max = 2; R = 5.

Статистический ряд с абсолютными частотами для исходной выборки:

yi	– 3	– 2	– 1	0	1	2
ni	1	1	3	2	2	1

Тот же ряд с относительными частотами примет вид:

yi	– 3	– 2	– 1	0	1	2
wi	0.1	0.1	0.3	0.2	0.2	0.1

Полигон относительных частот для рассматриваемого примера изображен на рис. 7.1 (Mathcad).

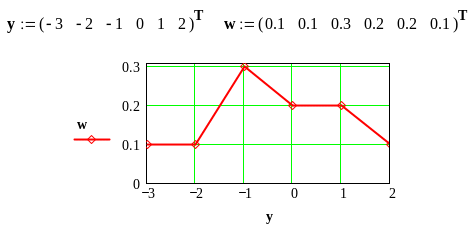
Рис. 7.1. Полигон относительных частот

Группированный ряд для данной выборки образуем, назначая в диапазоне выборочных данных три промежутка шириной ~ 1,67. Тогда группированный статистический ряд для нашего примера будет представлен таблицей вида:

zk	–2.17	0.5	1.17
nk	2	5	3

В таблице приведены средние значения промежутков и частоты.

Статистическое распределение выборки может быть охарактеризовано выборочной (эмпирической) функцией распределения.

Выборочной функцией распределения F_в(y₀) называется относительная частота события Y < y₀ , полученная для конкретной выборки. Согласно этому определению для выборки объема n имеем:

F_в(y₀) = .

Здесь w(Y < y₀) — относительная частота события Y < y₀, для получения которой в статистическом ряде, составленном для рассматриваемой выборки, просуммированы все относительные частоты, для которых y_i меньше заданного значения y₀.

Значения эмпирической функции распределения для выборки из примера 7.1 приведены на рис. 7.2 (Mathcad). Функция распределения, обозначенная в mcd-файле (см. рис. 7.2) как F, получена в виде вектора-столбца по результатам последовательного суммирования элементов вектора относительных частот из примера 7.1.

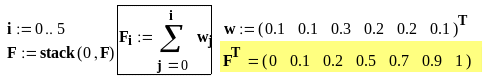
Рис. 7.2. Значения эмпирической функции распределения

Задание эмпирической функции распределения для примера 7.1 и ее графическая интерпретация представлены на рис. 7.3. Для задания F_в(y) использованы операторы Add Line и if программных блоков Mathcad, существенно упрощающие представление F_в(y) и построение графика.

Рис. 7.3. Задание эмпирической функции распределения

Основным свойством выборочной функции распределения служит то, что для любого фиксированного значения y₀ выборочная функция распределения F_в(y₀) стремится по вероятности к теоретической функции распределения случайной величины Y [3]. Из этого свойства следует, что выборочная функция распределения F_в(y₀) может служить приближенным значением (оценкой) теоретической функции распределения F(y₀) случайной величины Y, причем отличие значения F_в(y₀) от F(y₀) при увеличении объема выборки n будет уменьшаться.

Выборочные распределения имеют числовые характеристики, аналогичные подобным характеристикам с. в. В отличие от последних, характеристики выборочных распределений носят название выборочных числовых характеристик; их значения получают путем преобразований выборочных данных. Выборочные числовые характеристики всегда будут отличаться от соответствующих теоретических значений и, по этой причине, могут рассматриваться лишь как оценки истинных (теоретических) значений числовых характеристик распределений. Числовые характеристики выборочных распределений объединяются выборочными моментами, которые, как и теоретические моменты, подразделяются на начальные и центральные выборочные моменты распределений.

Выборочным начальным моментом k-го порядка называют взвешенную сумму вида:

. (7.1)

Весами в (7.1) служат относительные частоты w_i значений y_i.

Если все элементы выборки X имеют различные значения, n_i = 1 и выражение (7.1) упрощается:

. (7.2)

Начальный выборочный момент первого порядка носит название выборочного среднего:

, (n_i ≥ 1); (7.3)

, (n_i = 1). (7.4)

Для получения центральных выборочных моментов предварительно осуществляется операция центрирования, которая заключается в вычитании выборочного среднего (7.3), (7.4) из выборочных данных: .

Выборочным центральным моментом k-го порядка называют:

, (n_i ≥ 1); (7.5)

, (n_i = 1). (7.6)

Выборочное среднее относится к числу наиболее часто используемых числовых характеристик выборочных распределений. Другой числовой характеристикой выборочных распределений, которая также часто используется в практике статистического моделирования, служит выборочный центральный момент второго порядка или выборочная дисперсия:

, (n_i ≥ 1); (7.7)

, (n_i = 1), (7.8)

где — выборочное среднее квадратическое отклонение.

В математической статистике существует еще одна выборочная числовая характеристика — исправленная выборочная дисперсия:

, (n_i = 1), (7.9)

Как отмечалось, выборочные характеристики являются оценками соответствующих теоретических числовых характеристик:

‑ несмещенная оценка математического ожидания с. в. Х;

‑ смещенная оценка дисперсии с. в. Х;

s² ‑ несмещенная оценка дисперсии с. в. Х.

Кроме перечисленных, наиболее часто используемых числовых характеристик выборочных распределений, при сопоставительном анализе систем на основе статистического моделирования часто используется выборочный коэффициент вариации:

k_B = _B / . (7.10)

Пример 7.2. Найти значения выборочного среднего, выборочных дисперсий и коэффициента вариации выборки, рассмотренной в примере 7.1.

Решение. Для получения числовых характеристик воспользуемся приведенными выше формулами для выборочных моментов распределения, а так же — встроенными функциями Mathcad, которые реализуют соответствующие вычисления выборочных числовых характеристик (рис. 7.4). Для получения искомых числовых характеристик предварительно формируются (см. рис. 7.4, а) так называемые функции пользователя — выражения общего вида, последующее использование которых возможно при любом значении аргументов. С помощью функций пользователя в примере представлены начальные и центральные выборочные моменты k-го порядка.

Рис. 7.4, а. Формирование функций пользователя в среде Mathcad

Продолжение mcd-файла на рис. 7.4, а представлено на рис. 7.4, б, где по формулам (7.3)-(7.10) проводятся вычисления.

Выборочные числовые характеристики, вычисляются также с применением встроенных функций Mathcad, выделенных заливкой.

Рис. 7.4, б. Решение примера 7.2 в среде Mathcad

Как отмечалось выше, наряду с вариационным и статистическим рядами, выборки могут быть представлены и группированными статистическими рядами, т. е. серединами промежутков и частотами попадания выборочных данных в эти промежутки. Такое представление данных, полученных в эксперименте, несколько искажает информацию об исследуемой с. в., что отражается, прежде всего, на точности вычисления выборочных числовых характеристик. На рис. 7.5 представлен пример оценки уровня этих искажений при переходе к группированному статистическому ряду.

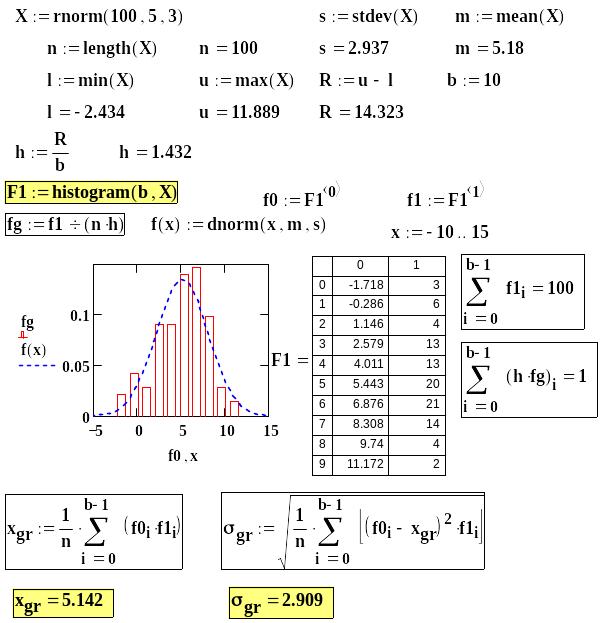
Рис. 7.5. Вычисления с группированным статистическим рядом

В качестве выборочных данных в mcd-файле использована совокупность нормально распределенных независимых случайных чисел, полученных от датчика (встроенная функция rnorm; n = 100). Теоретические значения математического ожидания и СКО заданы 5 и 3 соответственно. Выборочное среднее и выборочная СКО для данной выборки получены равными 5,18 и 2,937. В среде Mathcad группированный статистический ряд формируется встроенной функцией histogram, которая используется также и для построения гистограммы. Эта функция выводит двухстолбцовую матрицу (F1), первый столбец которой содержит середины промежутков, второй — частоты попаданий выборочных данных в эти промежутки. Число промежутков выбрано в примере равным 10.

Полученная матрица используется (см. рис. 7.5) для построения гистограммы и вычисления значений выборочного среднего (x_gr) и выборочной СКО (_gr). На гистограмму нанесена кривая плотности нормального распределения с полученными параметрами, для чего абсолютные частоты предварительно промасштабированы (разделены на произведение nh). Сопоставление значений числовых характеристик, полученных по исходной выборке и по группированному ряду, в данном примере показывает близость этих значений.