Задание двумерного случайного вектора

x2\ x1	х11	х12	…	х1 i1	…	х1k
x21	p(1, 1)	p(2, 1)	…	p(i1, 1)	…	p(k, 1)
x22	p(1, 2)	p(2, 2)	…	p(i1, 2)	…	p(k, 2)
…	…	…	…	…	…	…
x2 i2	p(1, i2)	p(2, i2)	…	p(i1, i2)	…	p(k, i2)
…	…	…	…	…	…	…
	p(1, m)	p(2, m)	…	p(i1, m)	…	p(k, m)

Определим, например, закон распределения первого элемента вектора (5.22). Для этого необходимо задать возможные значения и определить вероятности этих значений, т. е. вероятности появления событий , i₁ = ( ), i₂ = ( ) при любых значениях . Например, вероятность появления событий заключающихся в том, что при произвольных значениях , i₂ = ( ), будет равна сумме вероятностей, расположенных в первом столбце табл. 5.1:

=

= p(1, 1) + p(1, 2) + … + p(1, m) = . (5.25)

Выражение (5.25) следует из несовместности указанных событий, вероятность суммы которых определяется по теореме сложения вероятностей (2.2) как сумма вероятностей. Подобное выражение может быть составлено для любого значения . Поэтому вероятности событий могут быть найдены суммированием строк табл. 5.1:

. (5.26)

Вероятности распределения случайной величины (второго элемента вектора Х) будут результатом суммирования столбцов табл. 5.1:

. (5.27)

Выражения (5.26), (5.27) обобщаются следующим правилом ‑ для получения вероятностей ряда распределения одной из д.с.в. ‑ составляющих двумерного вектора (5.22) необходимо просуммировать вероятности совместного появления событий и по другой составляющей. Рассмотренное правило может быть обобщено на случай n-мерного случайного вектора.

Свойство 3. Для получения вероятностей ряда распределения (5.1) одной из составляющих n-мерного случайного вектора необходимо просуммировать вероятности совместного появления различных комбинаций значений элементов случайного вектора по остальным составляющим.

Это означает, что, например, для трехмерного вектора (5.21) с элементами , , , значения которых заданы множествами , , , i₁ = ( ), i₂ = ( ), i₃ = ( ), получается совокупность из g = kml комбинаций этих значений с таким же числом вероятностей для каждого из них, причём

; ;

; . (5.28)

Задание n-мерного распределения дискретного случайного вектора (5.21) позволяет обобщить понятия кумулятивной вероятности (4.2) и вероятности попадания случайной величины в диапазон. Рассмотрим это на примере двумерного случайного вектора (5.22).

Предположим, что возможные значения элементов и случайного вектора перечислены в возрастающем порядке, т. е. множества и ранжированы по возрастанию:

(5.29)

Тогда вероятность попадания двумерного случайного вектора (случайной точки на плоскости) в зону, соответствующую неравенствам , , выразится двойной суммой

(5.30)

т. е. суммой значений той части табл. 5.1, которая ограничена ее элементами и . Геометрически это означает вероятность попадания случайной точки в зону, изображенную на рис. 5.3, а.

Аналогично может быть выражена вероятность попадания случайной точки в зону, ограниченную, например, двусторонними неравенствами ; (см. рис. 5.3, б):

При n > 2 может быть решена задача о вероятности попадания случайной точки в подобные зоны ‑ объемы в n-мерном пространстве.

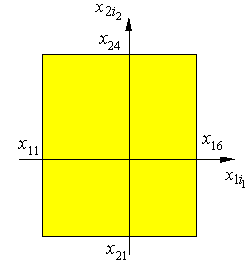
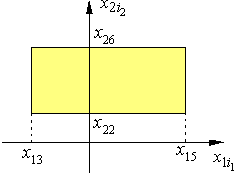
а б

Рис. 5.3. Области определения двумерной случайной величины