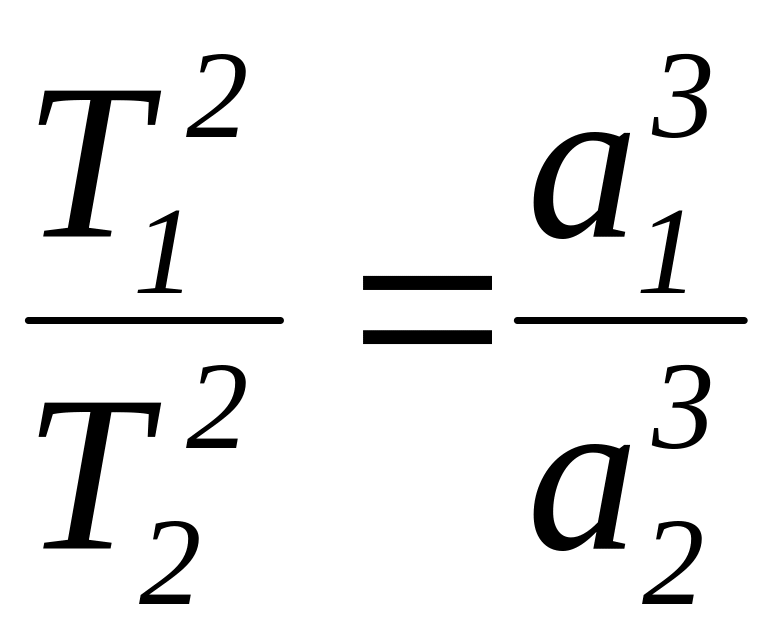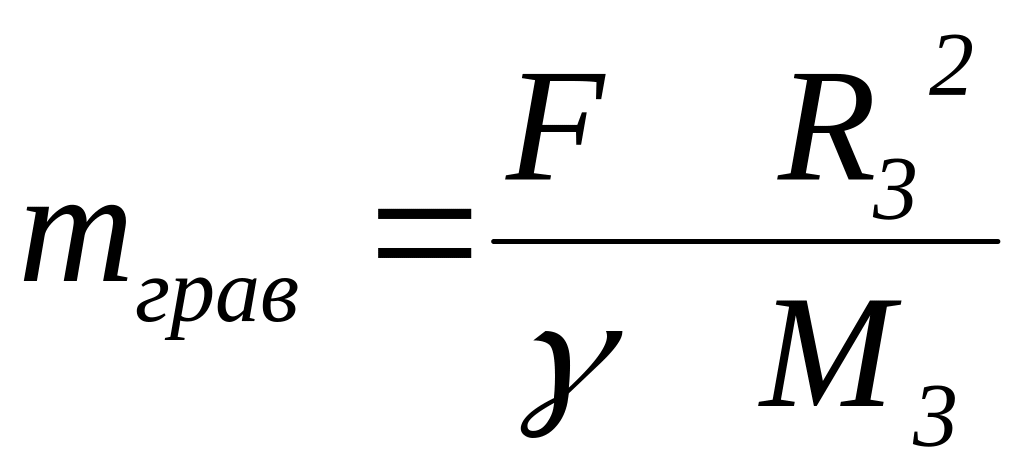5. Всесвітнє тяжiння

1.Закони кеплера і закон всесвітнього тяжіння.

Обробляючи результати багаторічних спостережень датського астронома Тихо Браге, Iоган Кеплер емпірично встановив три закони руху планет:

1). Кожна планета рухається по еліпсу, в одному з фокусів якого знаходиться Сонце.

2). Радіус - вектор планети за рiвнi проміжки часу описує однакові площi.

3). Квадрати перiодiв обертання планет відносяться як куби великих півосей еліптичних орбіт, по яким вони рухаються навколо Сонця.

(5.1)

Аналіз законів Кеплера привів Ньютона до відкриття закону всесвітнього тяжіння :

Два точкових тіла притягуються одне до одного з силами, прямо пропорційними добутку їх мас і обернено пропорційними квадрату відстані між ними.

,

або

(5.2)

Вказані сили називають гравітаційними або силами всесвітнього тяжіння. За сучасними уявленнями, взаємодія тіл здійснюється з допомогою гравітаційного поля, оточує всі матеріальні тіла.

Для обчислення сил взаємодiї не точкових тiл необхiдно розбити їх на частини, якi можна вважати матеріальними точками, розрахувати сили взаємодiї цих частин, а потім ці сили геометрично додати. В основі цього обчислення лежить принцип суперпозиції гравiтацiйних полів :

Гравiтацiйне поле, що збуджується якою-небудь масою, зовсім не залежить вiд наявності інших мас. Гравiтацiйне поле, створене декількома тілами, дорівнює геометричній сумі гравiтацiйних полiв, збуджених кожним з цих тiл.

Принцип суперпозиції є узагальненням досліду. Користуючись ним, можна довести, що двi однорiднi кулi притягуються мiж собою так, як нібито їх маси зосереджені в їх центрах.

Коефіцієнт пропорцiональностi в (5.2) називається гравiтацiйною сталою; вона дорівнює: Гравітаційна стала чисельно дорівнює силі, з якою притягуються два точкових тіла масами по 1 кг , розташовані на відстані 1 м один від одного.

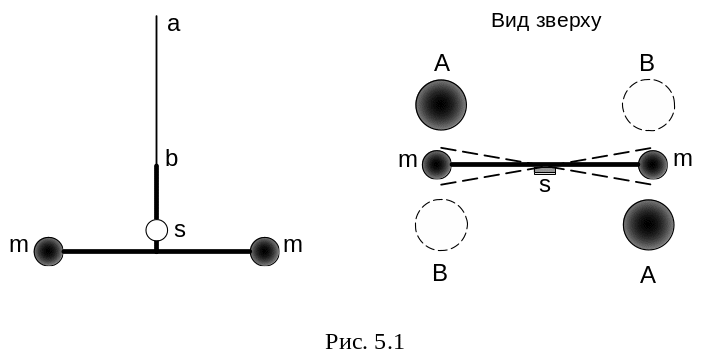
Як бачимо, гравiтацiйна стала досить мала. Тому i сили гравiтацiйної взаємодiї мiж звичайними тілами надзвичайно малi. Вперше виміряти силу взаємодії між звичайними тілами на Землі зумів англійський фізик Г.Кавендiш в 1798р. Прилад Кавендiша (див.рис.5.1) складався з легкого горизонтального стержня, на кінцях якого були закрiпленi двi однакові свинцеві кульки масою . Стержень пiдвiшувався на тонкій пружній нитці ab. До середини стержня прикріплювалось маленьке дзеркало s. Поблизу кульок розміщувались двi великі свинцеві кулі масами M спочатку в положеннi AA , потім в положенні ВВ. Завдяки гравiтацiйнiй взаємодiї кульок m i M стержень повертався на якийсь кут , що вимірювався за зміщенням променя

світла, відбитого від дзеркала S. Знаючи пружні властивості нитки, можна було визначити силу взаємодії кульок i обчислити значення гравiтацiйної сталої. Кавендiш одержав гарне, як на той час, значення:

.

Всі закони Кеплера можна одержати iз закону всесвітнього тяжіння Ньютона та законів збереження енергії i моменту iмпульсу (див. далi), якщо врахувати взаємодію планет лише iз Сонцем. Маса Сонця бiльш нiж в 700 раз перевищує загальну масу планет i всiх iнших тiл сонячної системи, тому Сонце є основним тiлом, що керує рухом планет. Проте кожна планета зазнає гравiтацiйного притягання також з боку iнших планет Сонячної системи; тому закони Кеплера є наближеними законами.

З закону всесвітнього тяжіння випливає, що гравiтацiйна сила пропорційна масі тiла, на яке вона дiє. Проте маса - це міра iнертностi тiла i з другого закону Ньютона вона може бути визначена так:

(5.3)

Цю масу назвали інертною масою.

З закону всесвітнього тяжіння масу тiла можна визначити, вимірюючи силу притягання його до Землi:

(5.4)

Цю масу називають гравітаційною масою. Вона є кiлькicною мірою гравітаційної взаємодії тiл.

Дослiди показали, що iнертнi маси всiх тiл в межах досягнутої точності вимірювань пропорційні їх гравiтацiйним масам. (Один з таких дослідів - перевірка незмінності прискорення вiльного падiння для всiх тiл). Тому значення інертної i гравітаційної мас можна прирівняти одну одній i в подальших міркуваннях говорити про масу, не вказуючи, про яку з них йде мова.