Некие лекции по элтеху / LECT_08

Переходные процессы в линейных электрических цепях.

Определения

1. Коммутация – это какое-либо включение, выключение, переключение пассивных и активных ветвей и элементов схемы, приводящее к изменению конфигурации схемы или ее параметров. Предполагается, что коммутация совершается мгновенно (время коммутации равно нулю). Момент времени непосредственно до коммутации называется: 0_‑ (“минус ноль”, момент непосредственно после: 0₊ (“плюс ноль”).

Для схемы до коммутации и после коммутации характерны некоторые установившиеся режимы. В результате коммутации в схеме возникает некий режим перехода от установившегося процесса до коммутации к установившемуся процессу после коммутации. Это и есть переходный процесс. Теоретически длительность переходного процесса равна бесконечности, т.е. режим в цепи асимптотически приближается к установившемуся. Практически малым отличием режима от установившегося пренебрегают, и считают, что длительность переходного процесса конечна.

Законы коммутации

1. В индуктивном элементе ток и магнитный поток в момент коммутации не изменяются, т.е.

(1)

Ток индуктивности сразу после коммутации равен току индуктивности непосредственно перед коммутацией (то же для магнитных потоков). В переходном процессе ток индуктивности и ее магнитный поток изменяются, начиная с этого значения.

2. Напряжение емкостного элемента и его заряд в момент коммутации не изменяются.

(2)

Напряжение на емкости и ее электрический заряд сразу после коммутации равны напряжению на емкости и электрическому заряду непосредственно перед коммутацией. В переходном процессе напряжение на емкости и ее электрический заряд изменяются, начиная с этого значения.

Обоснование законов коммутации

Если в момент коммутации меняется скачком, то и, следовательно, из-за чего нарушается второй закон Кирхгофа, чего не может быть.

Аналогично.

Если в момент коммутации меняется скачком, то и, следовательно, из-за чего нарушается первый закон Кирхгофа, чего не может быть.

Обоснование законов коммутации из закона сохранения энергии.

Энергия магнитного поля индуктивности:

Энергия электрического поля емкости:

,

- мощность.

, , если или меняются скачком, то соответствующая мощность и стремятся к , следовательно, для скачкообразного изменения или схему надо подключить к источнику питания бесконечной мощности, чего быть не может.

Сформулированные законы коммутации не являются универсальными: существуют схемы, для которых они не выполняются. Эти схемы называются некорректными, для их расчета существуют специальные методы.

Значения в начальный момент времени токов индуктивностей и напряжений на ёмкостях называются независимыми начальными условиями. Значения других величин в начальный момент времени , , , называются зависимыми начальными условиями, они могут изменяться скачком в момент коммутации и определяются по независимым начальным условиям с помощью первого и второго закона Кирхгофа.

Зависимость токов и напряжений в схеме от времени представляем в виде суммы двух составляющих: принужденной и свободной:

, . (3)

Принужденная составляющая описывает установившийся режим цепи после коммутации, она определяется свойствами цепи и источника питания. Если источник постоянный, то установившийся режим постоянный и принужденная составляющая постоянная. Если источник периодический, то установившийся режим и принужденная составляющая ‑ периодические.

Свободная составляющая отражает зависимость переходного процесса от свойств цепи – конфигурации и параметров.

Математически переходный процесс в линейной схеме описывается линейным обыкновенным дифференциальным уравнением с постоянными коэффициентами n-ого порядка, где n число индуктивностей и емкостей в схеме, т.е. элементов, накапливающих энергию, источники напряжения и тока входят в правую часть этого ОДУ. Принужденная составляющая является частным решением неоднородного ОДУ, свободная составляющая – общим решением однородного ОДУ. Для ОДУ n-ого порядка требуется n начальных условий. Они могут быть получены из n независимых условий: токов индуктивностей и напряжений емкостей в момент коммутации.

Метод расчета переходных процессов в линейных цепях состоящий в поиске решения ОДУ n-ого порядка называется классическим методом расчета переходных процессов. При этом само ОДУ в явном виде не записывается.

Пример 1

Включение RC-цепи на постоянное напряжение.

Найти , ключ замыкается

В замкнутом состоянии цепь является контуром, запишем для него второй закон Кирхгофа:

, т.к.

т.е.

Это ОДУ - линейное с постоянными коэффициентами.

Принужденное напряжение – частное решение неоднородного ДУ ‑ ищем в виде константы:

:

Общее решение однородного уравнения будет иметь вид:

- постоянная времени.

Постоянная B ищется из нескольких условий: по закону коммутации , до коммутации ключ был разомкнут и все напряжения в схеме были равны нулю (она была отключена от источника)

Это и есть начальное условие для нашей задачи.

Решение ищем в виде:

отсюда

, (4)

Пример 2

Ключ замыкается

По законам Кирхгофа составим систему ОДУ:

;

(5)

,

откуда

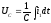
подставим в систему уравнений и продифференцируем по t:

(6)

Независимые начальные условия

;

определим из схемы до коммутации

ввиду того, что , , , постоянный ток через ёмкость не течет.

Запишем искомую величину в виде суммы свободной и принужденной составляющей:

Принужденная составляющая есть установившаяся составляющая после коммутации, когда переходный процесс закончился.

,

Постоянный ток через емкость не течет.

Чтобы найти свободную составляющую переходного процесса, которая является общим решением однородного уравнения, необходимо записать характеристическое уравнение системы ОДУ (или ОДУ ей эквивалентного) и найти его корни. Из системы (6) можно исключить и , и для полученного ОДУ записать характеристическое уравнение. Но можно составить главный определитель системы (5) и приравнять его нулю:

отсюда

Корни характеристического уравнения:

- соответствует установившемуся режиму. Два других найдем из уравнения

или

Дискриминант этого квадратного уравнения имеет вид:

1) - корни действительные, разные

2) - корни действительные, одинаковые

3) - корни комплексные сопряженные

В первом случае свободная составляющая имеет вид

Во втором случае:

В третьем случае:

- есть действительная часть корней, _св – модуль мнимых частей корней.

Пусть в нашем случае корни действительные, различные, тогда, с учетом:

,

решение примет вид:

Для определения постоянных интегрирования и , запишем значение и его производную в начальный момент времени:

значения и определим из системы (5), записанной для начального момента времени :

.

Из законов коммутации:

,

тогда:

,

Для определения начального значения производной продифференцируем систему (5) и подставим

отсюда

из второго уравнения исходной системы при

Алгебраические уравнения для постоянных интегрирования: