Некие лекции по элтеху / rezonans

ЯВЛЕНИЯ РЕЗОНАНСА

РЕЗОНАНС НАПРЯЖЕНИЙ

Рассмотрим контур, состоящий из последовательно соединенных сопротивления, индуктивности и емкости (рис. 1)

Рис. 1. Последовательный контур.

Напомним принятые обозначения:

1. строчными буквами обозначаются мгновенные значения: u, i, u_L, u_C;

2. заглавными буквами обозначаются действующие значения: U, I, U_L, U_C;

3. подчеркнутыми заглавными буквами - комплексные действующие значения: U, I, U_L, U_C.

Входное сопротивление контура:

.

Комплексное действующее значение тока контура имеет вид:

,

отсюда получается действующее значение тока

.

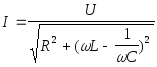Аналогичным образом получаются выражения для действующих значений напряжений на индуктивности (U_L, U_L) и на емкости (U_C, U_C).

;

.

Условием наступления резонанса напряжений является равенство нулю реактивной составляющей входного сопротивления контура:

.

При резонансе реактивные сопротивления индуктивности и емкости равны:

,

эта величина называется характеристическим сопротивлением контура.

Отношение характеристического сопротивления контура к его омическому сопротивлению называется добротностью контура:

.

Заметим, что при =₀ отношение действующих значений напряжений на индуктивности и на емкости к действующему значению входного напряжения равно добротности:

.

Преобразуем выражение для действующего значения тока контура, вынеся активное сопротивление R за знак радикала а характеристическое сопротивление =₀L за скобки и учитывая определение Q:

.

Аналогичным образом получаем выражения для действующих значений напряжений на индуктивности и на емкости:

.

Введя относительную частоту _*=/₀, преобразуем полученные формулы к следующему виду:

Найдем точки максимумов этих трех кривых.

Очевидно, что при резонансной частоте полное входное сопротивление контура (z=Z) минимально и равно активному сопротивлению, тогда действующее значение тока максимально и равно:

Чтобы найти точки максимумов кривых U_L() и U_C() необходимо продифференцировать их по частоте, например:

приравняв к нулю числитель полученной дроби, уравнение для частоты максимума для действующего значения напряжения на индуктивности:

,

таким образом, частота максимума действующего значения напряжения на индуктивности равна:

.

Аналогично, частота максимума действующего значения напряжения на емкости равна:

.

Отметим, что: _L>₀, _C<₀, _L_C=₀². Если Q<1/2, то _L и _C - мнимые, т.е. кривые U_L() и U_C() не имеют максимумов.

Рассмотрим зависимость I() (рис. 2). Полосой пропускания называется частотный диапазон ₁₂, в котором выполняется условие:

.

Уравнение для границ полосы пропускания имеет вид:

.

Это - уравнение четвертого порядка, два корня которого являются границами полосы пропускания и имеют вид (два других корня - отрицательные и не имеют физического смысла):

.

Легко видеть, что: ₁₂=₀².

Рис. 2.

На рис. 2 представлены зависимости от нормированной частоты действующих значений (амплитуд): тока - сплошная линия, напряжения на емкости - штриховая линия, напряжения на индуктивности - пунктирная линия, а также разности фаз входного напряжения и тока (=_u-_i) - штрих-пунктирная линия при добротности Q=2.

На рис. 3 представлены зависимости от нормированной частоты отношений действующих значений (амплитуд) тока к действующему значению (амплитуде) тока на резонансной частоте для различных значений добротности: при Q=0.5 - сплошная линия, при Q=1 - пунктирная линия, при Q=10 - штриховая линия. Из рисунка видно, что чем больше добротность, тем лучше избирательные свойства цепи: т.е. цепь лучше выделяет сигнал определенной частоты из суммы сигналов различных частот.

Рис. 3.

РЕЗОНАНС ТОКОВ

Рассмотрим параллельный контур (рис. 4).

Рис. 4

Вычислим входную проводимость схемы:

Резонанс наступает, когда реактивная часть входной проводимости становится равной нулю:

Вводя обозначения:

,

получим:

.

Резонанс возможен, если одновременно R₁> и R₂> или R₁< и R₂<, если R₁<, а R₂> или наоборот, то резонансная частота - мнимая, т.е. резонанс не наступает, если же R₁=R₂=, то _Р=0/0, т.е. резонанс наступает при любой частоте. Рассмотрим входное сопротивление контура в этом случае:

Т.о. входное сопротивление контура равно  и от  не зависит.

На рис. 5, а, б показаны векторные диаграммы резонанса в идеальном (R₁=R₂=0) и реальном контурах. Если R₁=R₂=0, то активная входная проводимость равна нулю, резонансная частота _Р=₀, токи индуктивности и емкости равны и противоположны по фазе, входной ток равен нулю.

а) идеальный контур	б) реальный контур

Рис. 5.

ПОНЯТИЕ О РЕЗОНАНСЕ В СЛОЖНЫХ ЦЕПЯХ

Условие резонанса b=0 или x=0 в разветвленной цепи с несколькими индуктивностями и емкостями дают для частоты  уравнения, которые могут иметь несколько действительных корней, т.е. у разветвленной цепи может быть несколько резонансных частот.

Пример.

Найдем входное сопротивление цепи, изображенной на рис. 6.

Рис. 6.

Если Z=0, наступает резонанс напряжений:

Входная проводимость этой цепи равна:

При Y=0 наступает резонанс токов:

.

Задача (4.88, Поливанов).

Для схемы рис. 7 даны L,C. При каком R входное сопротивление чисто активное на любой частоте?

Рис. 7.

Входное сопротивление равно:

Найдем величину R из условия равенства нулю мнимой части:

Т.о. получаем, что если активное сопротивление равно характеристическому, резонанс наступает на любой частоте.

Задача.

Найти L₀, при котором фазы u и i совпадают. R=2 Ом, L=2 мГн, C=250 мкФ, =210³ с^-1.

Рис. 8.

Входное сопротивление равно:

.

Чтобы фазы входного напряжения u и входного тока i совпадали, необходимо, чтобы реактивная составляющая входного сопротивления была равна нулю:

.

Резонанс токов наступает, если реактивная составляющая входной проводимости равна нулю:

,

отсюда:

.