
- •Синтез и кинематическое исследование рычажного механизма.
- •Структурный анализ и определение класса механизма.
- •Построение кинематической схемы механизма.
- •Построение плана скоростей для исследуемого положения механизма.
- •Построение плана ускорений для исследуемого положения механизма.
- •1.5. Построение диаграммы перемещения н ползуна в функции угла поворота кривошипа .
- •Кинетостатический расчет механизма (положение 1)
- •2.1.Силовой расчет структурной группы .
- •2.2. Силовой расчет структурной группы ab .
- •2.3. Силовой расчет звена 1 (оа).
Кинетостатический расчет механизма (положение 1)
Кинетостатическим называется силовой расчет механизмов, если в число заданных сил входят и силы инерции звеньев. А если силы инерции не входят, то силовой расчет позволяет найти реакции в кинематических парах, т.е. определить те давления, которые возникают в местах соприкосновения элементов кинематических пар, а также найти уравновешивающую силу и уравновешивающий момент пары сил.
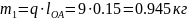 (2.1)
(2.1)
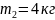 (2.2)
(2.2)
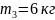 (2.3)
(2.3)
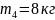 (2.4)
(2.4)
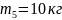 (2.5)
(2.5)
где q=9…12 кг/м;
2.1.Силовой расчет структурной группы .
Силовой расчет начинаем с последней присоединенной группы.
В масштабном коэффициенте вычерчиваем отдельно схему структурной группы в положении, для которого строили план ускорений.
B – внешняя вращательная кинематическая пара присоединения группы
C – внутренняя вращательная пара соединения звена 4 (BC) с ползуном 5.
 – внешняя
поступательная кинематическая пара
соединения ползуна с направляющей
поверхностью Х-Х
– внешняя
поступательная кинематическая пара
соединения ползуна с направляющей
поверхностью Х-Х
2.1.1.Определяем инерционные нагрузки.
Силы инерции каждого звена определяются по формуле:
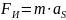 (2.6)
(2.6)
где
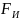 – сила инерции звена, Н;
– сила инерции звена, Н;
m – масса звена, кг;
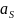 – ускорение
центра масс звена,
;
– ускорение
центра масс звена,
;
Сила инерции звена 4 и 5 определяется:
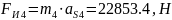 (2.7)
(2.7)
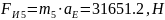 (2.8)
(2.8)
2.1.2. Так как звено 4 вращается неравномерно, то возникает момент силы инерции,
который определяется:
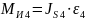 (2.9)
(2.9)
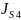 – момент
инерции звена 4, относительно оси,
проходящей через центр масс звена и
перпендикулярной к плоскости вращения
звена,
– момент
инерции звена 4, относительно оси,
проходящей через центр масс звена и
перпендикулярной к плоскости вращения
звена,
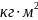 ;
;
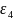 -
угловое ускорение звена 4, 1/
;
-
угловое ускорение звена 4, 1/
;
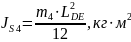 (2.10)
(2.10)
=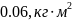
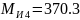
2.1.3. Силу тяжести определим по формуле:
G=m g
(2.11)
g
(2.11)
где m – масса звена, кг;
g – ускорение свободного падения, ;
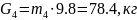 (2.12)
(2.12)
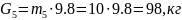 (2.13)
(2.13)
2.1.4.
Запишем для структурной группы
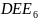 условие равновесия и составим уравнение
равновесия:
условие равновесия и составим уравнение
равновесия:
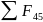 =0
=0
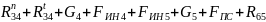 =0
(2.14)
=0
(2.14)
где
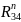 - нормальная составляющая реакции звена
4 в точке (D),
H;
- нормальная составляющая реакции звена
4 в точке (D),
H;
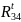 – касательная
составляющая реакции звена 4 в точке
(D),
H;
– касательная
составляющая реакции звена 4 в точке
(D),
H;
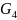 – сила
тяжести звена 4, Н;
– сила
тяжести звена 4, Н;
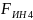 -
сила инерции звена 4, Н;
-
сила инерции звена 4, Н;
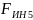 -
сила инерции звена 5, Н;
-
сила инерции звена 5, Н;
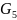 -
сила тяжести звена 5, Н;
-
сила тяжести звена 5, Н;
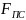 – сила
полезного сопротивления по условию
задания, Н;
– сила
полезного сопротивления по условию
задания, Н;
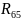 -реакция
опоры 6 на звено 5, Н;
-реакция
опоры 6 на звено 5, Н;
Значение касательной составляющей реакции точки D определим из уравнения равновесия звена 4, составленного в форме моментов всех сил структурной группы ,
действующих относительно точки Е.
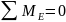

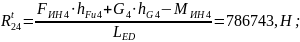 (2.15)
(2.15)
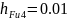 (2.16)
(2.16)
 (2.17)
(2.17)
Определим масштаб плана сил.
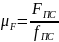 =
= , Н/мм (2.18)
, Н/мм (2.18)
где
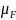 - масштаб сил, Н/мм;
- масштаб сил, Н/мм;
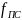 -
значение силы полезного сопротивления
на плане сил, берем 100 мм.
-
значение силы полезного сопротивления
на плане сил, берем 100 мм.
Определяем длины отрезков, которые будут отображать соответствующие силы на плане сил группы .
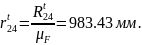 (2.19)
(2.19)
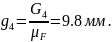 (2.20)
(2.20)
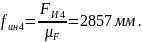 (2.21)
(2.21)
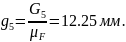 (2.22)
(2.22)
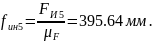 (2.23)
(2.23)
Измеряем
на плане сил длины отрезков, соответствующих
векторам реакций
,
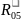 ,
,
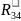 и умножив на масштаб плана сил
найдем их действительные значения:
и умножив на масштаб плана сил
найдем их действительные значения:
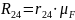 =8400,
Н
(2.24)
=8400,
Н
(2.24)
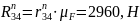 (2.25)
(2.25)
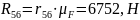 (2.26)
(2.26)
