Лабораторна робота №1.

Ознайомлення з інтегрованою системою аналізу і управління даними STATISTICA. Основні модулі системи STATISTICA. Перемикач модулів Module Switcher.

Мета роботи:

• получить общее представление о способах работы с системой, включая интерак­тивное взаимодействие при помощи команд меню, использование различных типов макрокоманд, возможностях командного языка SCL и языка STATISTICA BASIC;

• получить общий обзор способов ввода исходных данных для статистического анали­за, их подготовки и визуализации, а также способов вывода результатов статис­тического анализа в виде таблиц и графиков;

• получить представление об основных статистических модулях и конкретных статис­тических процедурах, реализованных в них;

Програма виконання лабораторної роботи

1. Перед виконанням роботи необхідно ознайомитись з матеріалами для самостійної роботи ( частина 1і 2).

2. Виконати приклади, які наведені в розділі 1.

3. Самостійно виконати завдання на створення таблиць.

4. Перевірити свої знання за контрольними питаннями.

1. Вводные примеры

1.1. Введение

В этом разделе будут детально разобраны два законченных примера обработки реаль­ных данных в системе STATISTICA.

Основная цель раздела

Основное внимание будет уделено технологии обработки данных. Мы покажем, из каких основных шагов состоит процесс обработки данных в системе, проиллюстрируем некоторые возможности системы STATISTICA по работе с данными, выводу графиков, проведению анализа и выводу его результатов. Разбор этих примеров является важным этапом освоения системы, так как позволяет изучить и понять весь процесс обработки данных в целом.

Основные шаги обработки данных в системе

Статистическая обработка данных в системе STATISTICA обычно состоит из сле­дующих основных шагов:

• ввод исходных данных в электронную таблицу системы STATISTICA;

• предварительные преобразования данных перед непосредственным применением конкретного статистического метода;

• визуализация данных при помощи того или иного типа графиков;

• статистический анализ при помощи некоторого статистического метода. Подбор модели и задание необходимых параметров в статистических процедурах;

• вывод численных, текстовых и графических результатов, как на рабочее простран­ство системы, так и в файл с отчетом;

• анализ результатов.

На основе простейшего примера статистической обработки — линейной регрессион­ной модели — мы проиллюстрируем эти основные этапы обработки.

1.2. Обработка данных в рамках линейной регрессионной модели

1.2.1. Линейная регрессия. Подбор прямой Формулировка задачи

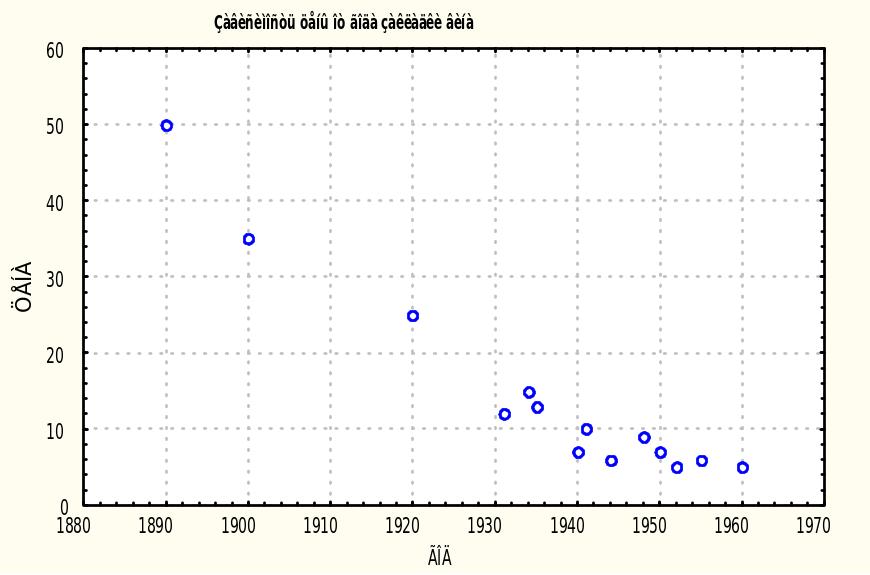
В качестве примера рассмотрим данные, опубликованные в газете The Chicago Maroon за пятницу 10 ноября 1972 г. (этот пример взят нами из книги [8] , стр. 88). В ней сообщались оптовые цены на марочные вина в зависимости от года закладки вина. Цены указаны в долларах за одну бутылку. Приводились следующие данные:

ГОД	ЦЕНА
1890	50.00
1900	35.00
1920	25.00
1931	11.98
1934	15.00
1935	13.00
1940	6.98
1941	10.00
1944	5.99
1948	8.98
1950	6.98
1952	4.99
1955	5.98
1960	4.98

Таблица 2.1. Исходные данные для анализа

Естественно предположить, что между возрастом вина и его стоимостью имеется не­которая зависимость. Интуитивно понятно, что чем больше выдержка, тем вино должно быть дороже. Данные показывают, что в общем эта тенденция выполняется, однако имеются и исключения. Итак, мы хотим приближенно выразить зависимость между эти­ми двумя переменными. Зачем это нужно ? Например, имея такую формулу, можно про­гнозировать стоимость вин на следующем аукционе (в 1973 году) или, если вы плани­руете продавать вино, года закладки которого нет в таблице (например 1945), вы можете грамотно назначить на него цену.

Математическая постановка задачи

Одна из наиболее распространенных задач статистического исследования состоит в изучении связи между некоторыми наблюдаемыми переменными. Регрессионный анализ предназначен для изучения связей между одной зависимой и несколькими (или одной, как в нашем примере) независимыми переменными. В линейном регрессионном анализе эта связь предполагается линейной. В самом простом случае в линейной регрессионной модели имеются две переменные Х и Y. И требуется по n парам наблюдений (X₁, Y₁), (X₂, Y₂) … (X_n, Y_n) построить (подобрать) прямую линию, которая "наилучшим образом" приближает наблюдаемые значения. Понятие "наилучшим обра­зом" может быть определено по - разному, однако на этом мы останавливаться не будем. Математически эта задача может быть сформулирована следующим образом: значениям независимой переменной Х отвечают значения зависимой переменной Y :Y_i=_i*X_i + ₀ + _i; i=1, … n, (*)где _i есть независимые случайные ошибки со средним 0 , которые интерпретируются как ошибки наблюдений, ₁, ₀ — неизвестные параметры, описывающие прямую линию и которые следует оценить по наблюдениям(X_i, Y_i), i=1, … n.

Приведенное выше уравнение называется уравнением регрессии.

В нашем примере независимая переменная — год закладки (или выдержка, которая равна возрасту вина), а зависимая переменная — его цена на аукционе. Иногда исполь­зуется и другая терминология. Зависимая переменная часто называется откликом, а независимые переменные — предикторами, контролируемые переменные — факторами. Эта терминология подчеркивает, что ряд переменных оказывают влияние на одну переменую — отклик.

В результате исследований мы, конечно, не сможем найти точные значения параметров ₁, ₀, однако можно получить их оценки, которые мы будем обозначать через b₁, b₀ и которые являются приближениями к значениям неизвестных параметров.

После того как оценки получены, мы можем записать уравнение связи в виде (1)

Заметим, что уравнение (1) позволяет нам найти оценку отклика при любом значении контролируемой переменной.

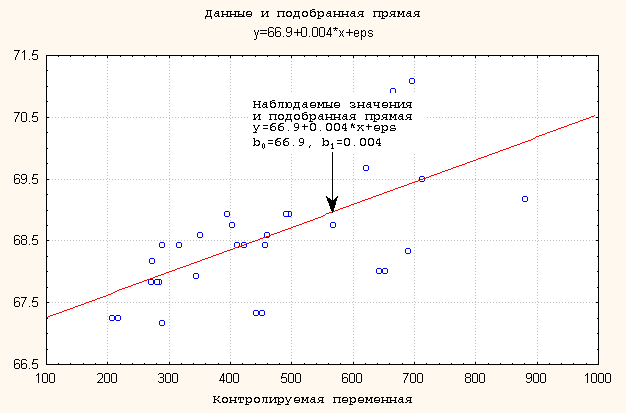
Рисунок 2.2. Необходимо подобрать прямую, которая приближает наблюдаемые данные