1. Коды Боуза – Чаудхури– Хоквингема (бчх-коды)

Довольно долго не удавалось получить обобщение кода Хэмминга на случай кратных ошибок. Это удалось сделать Р.К.Боузу и Д.К.Рой-Чаудхури, которые использовали тот факт, что на множестве двоичных слов можно ввести структуру конечного поля.

Пример. Ниже приведена табл. 2 для описания поля из 24 элементов .

Таблица 2

Поле

0			1								1000
1											0100
2											0010
3											0001
4			1	+							1100
5						+					0110
6								+			0011
7			1	+				+			1101
8			1			+					1010
9								+			0101
10			1	+		+					1110
11						+		+			0111
12			1			+		+			1111
13			1			+		+			1011
14			1					+			1001

В таблице элементы поля представлены как степени примитивного элемента (2-й столбец) и как многочлены степени не выше 3 от – корня неприводимого полинома . В последнем столбце представлены только коэффициенты этих многочленов – двоичные слова. Таким образом, на множестве двоичных слов, помимо операции поразрядного сложения по модулю два, может быть введена операция умножения. Например, по таблице находим

,

так как .

Покажем теперь, как строятся коды с исправлением 2-х, 3-х, вообще, любого фиксированного числа ошибок. По-прежнему считая, что построим проверочную матрицу , добавляя к матрице кода Хэмминга новые строки, так чтобы в новой матрице были линейно независимы каждые столбцов.

Теорема 1 (Боуз-Чаудхури). Линейный код с проверочной матрицей

(2)

исправляет ошибок.

Доказательство. Возьмем в матрице любые столбцов, пусть

номера этих столбцов. Обозначим

.

Очевидно, – различных двоичных слова длины или различных элемента поля . Допустим, что некоторая линейная комбинация выбранных столбцов равна нулю и обозначим коэффициенты этой линейной комбинации ( ). Тогда

(3)

Выше, в разделе, посвященном конечным полям, было выведено правило возведения в квадрат в поле характеристики 2:

(удвоенных произведений нет, так как ). Возводя в квадрат соотношения (3) и учитывая: что , так как , получим, что соотношения (3), записанные для нечетных степеней , равных , выполняются и для четных степеней

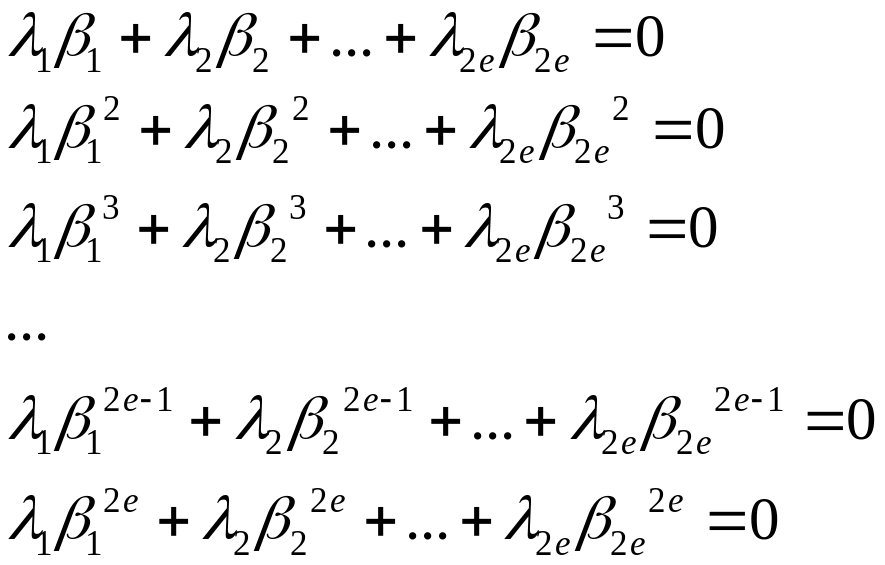(4)

Соотношения (1.4) представляют собой линейную однородную систему из уравнений относительно неизвестных . Определитель этой системы

представляет собой известный определитель Вандермонда и равен

.

Так как не равны нулю и различны, то определитель системы (4) отличен от нуля, откуда следует, что система (4) имеет только нулевой решение , то есть выбранные столбцы линейно независимы.