3. Число элементов конечного поля

Пусть – конечное поле с характеристикой равной простому числу . Как мы видели выше, поле содержит простое подполе . Будем сейчас рассматривать следующим образом: – это множество, на котором определена операция сложения элементов и операция умножения элементов на элементы из (То есть мы сейчас считаем, что операция умножения, имеющаяся в , действует только на парах элементов, один из которых входит в , а другой может быть любым элементом из ). Из аксиом поля 1-4,5 и 9 вытекает, что для множества с введенными таким путем операциями выполнены все аксиомы линейного (векторного) пространства над полем (рассматриваемого как поле скаляров). Так как конечно, то построенное векторное пространство имеет некоторую конечную размерность , базис . Каждый элемент однозначно записывается в виде

.

Это означает, что можно установить биекцию между элементами поля и словами длины в алфавите :

.

Так как число таких слов равно , то получаем следующую теорему.

Теорема 2. Число элементов конечного поля равно , где – простое число, a .

Лекция 9 Кольцо многочленов над полем. Алгоритм Евклида. Неприводимые многочлены

1. Кольцо многочленов над полем

Пусть – произвольное поле. Символом обозначают совокупность всех многочленов от переменной (всевозможных степеней), коэффициенты которых берутся из поля :

На этом множестве определены две операции: два многочлена можно сложить и перемножить по известным правилам. Операции сложения и умножения многочленов удовлетворяют аксиомам 1-7 и 9 поля (то есть всем, кроме восьмой). Как говорилось выше, такая совокупность объектов называется кольцом. Итак, – кольцо многочленов над полем .

Другим примером кольца является кольцо целых чисел . Оказывается, что основные свойства целых чисел являются следствиями аксиом 1-7, 9, и поэтому остаются справедливыми в любом кольце. В частности, перенесем на многочлены свойства целых чисел, связанные с делимостью. Степень многочлена будем обозначать .

Делимость многочленов

Говорят, что многочлен делится на многочлен , если можно найти такой многочлен , что . Говорят также, что делит и записывают это в виде .

Деление с остатком

Для любых двух многочленов и , можно найти такие многочлены и , что

(3)

Многочлены и могут быть найдены известным алгоритмом деления "уголком". Заметим, что вычисления упрощаются, если старший коэффициент делителя . Этого всегда можно добиться, вынося за скобки: . Здесь – делитель со старшим коэффициентом 1, a – новое частное, по которому, если необходимо, можно восстановить .

Для машинных вычислений удобна такая схема.

Вычислительная схема деления с остатком

Пусть

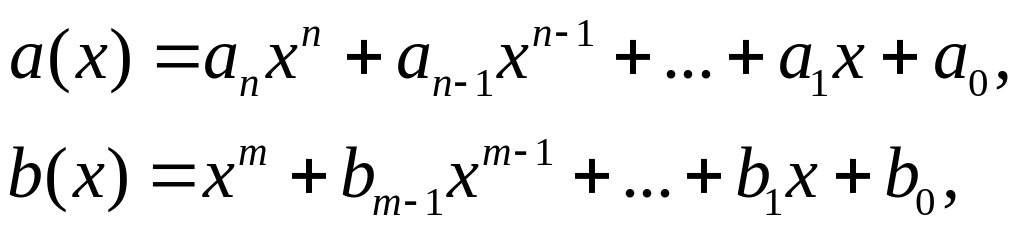(4)

( ). Будем считать, что , в противном случае и . Сравнение степеней в (3) показывает, что – многочлен степени , кроме того, – многочлен степени не выше чем :

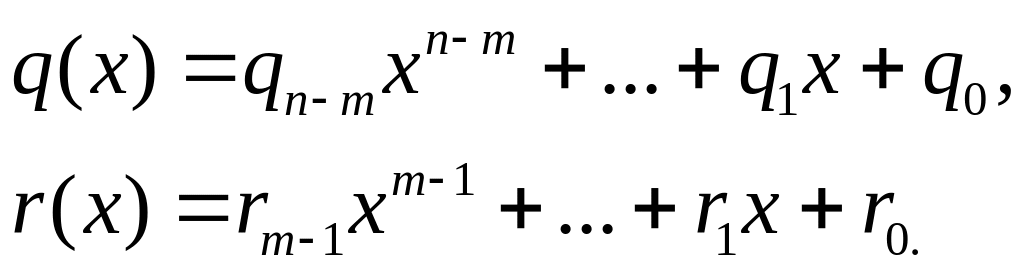(5)

Подставляя (4) и (5) в (3) и сравнивал коэффициенты при , получаем систему

. (6)

. (7)

Условие суммирования в этих суммах состоит в том, что индексы коэффициентов должны находиться в пределах от 0 до степени многочлена:

.

Следовательно, индекс суммирования должен изменяться в пределах

.

Например, при (6) принимает вид , то есть .

Если , то , следовательно,

,

так как . Заметим, что под знак суммы входят с индексами, большими , что дает возможность последовательно их вычислять. Таким образом, коэффициенты частного и остатка при делении двух многочленов можно найти по следующей схеме:

1°. Полагаем .

2°. Для вычисляем и полагаем

.

3°. Для вычисляем и полагаем

.

Утверждения о многочленах

Из формулы (3) деления с остатком вытекают известные факты о многочленах, для нас важно, что эти факты справедливы для кольца многочленов над произвольным полем.

1. Теорема 1(Безу). Пусть и а произвольный элемент поля . Тогда остаток от деления на многочлен равен элементу .

Действительно, записывая (2.3) для данного случая, получаем

,

где многочлен нулевой степени, то есть элемент поля . Подставляя в это равенство , получаем .

2. Если , то есть – корень , то делится на .

Это прямо следует из 1.

3. Многочлен степени в любом поле имеет не более корней.

Следует из того, что после деления на степень многочлена уменьшается на 1.

4. Если многочлен делится на :

,

и частное снова делится на , то будет делиться на . В этом случае корень называется кратным. Определяя формальную производную многочлена как многочлен , нетрудно проверить, что все правила дифференцирования остаются в силе. Например, если

,

то

.

Следовательно, если кратный корень многочлена, то многочлен и его производная делятся на . Наоборот, если известно, что у многочлена и его производной нет общих делителей степени выше нулевой, то все корни многочлена различные.